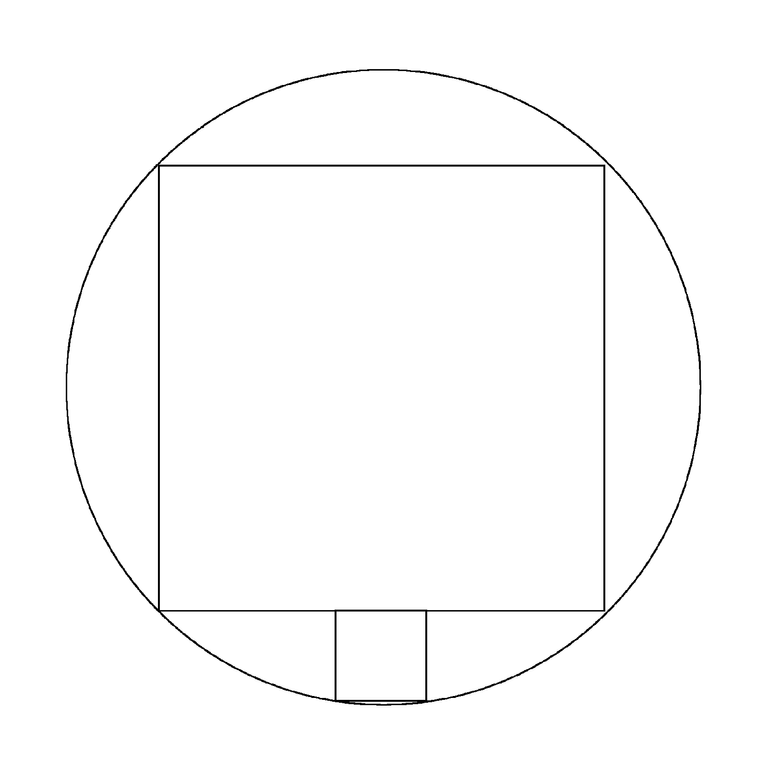
I came across this interesting geometrical problem the other day. The problem uses only secondary school algebra and geometry, but it stumped some Stanford graduate. For me, it took me 15 minutes to figure out.
The Problem
We have a big square inscribed within a circle, and a smaller square, incribed in one of the spaces between the big square and the circle, as shown in the diagram. The question is: what is the exact ratio of the radius of the circle to the length of a side of the smaller square?
The Struggle
Think!
.
.
.
think
.
.
.
think
.
.
.
Let r be the radius of the circle.
Let s be the length of a side of the smaller square.
The question is about finding r : s, or equivalently, 
.
.
.
think
.
.
.
think
.
.
.
think
.
.
.
maybe we can form some equations
.
.
.
think
.
.
.
think
.
.
.
what do we know? the corner of the large square exactly touches the circle ... kind of helpful, eh? but how so?
.
.
.
think
.
.
.
think
.
.
.
The Solution, Stage 1
We can drop a perpendicular from the centre O to one of the sides, we call F the foot of the perpendicular and we label one of the corners of the large square as A. See the diagram below.
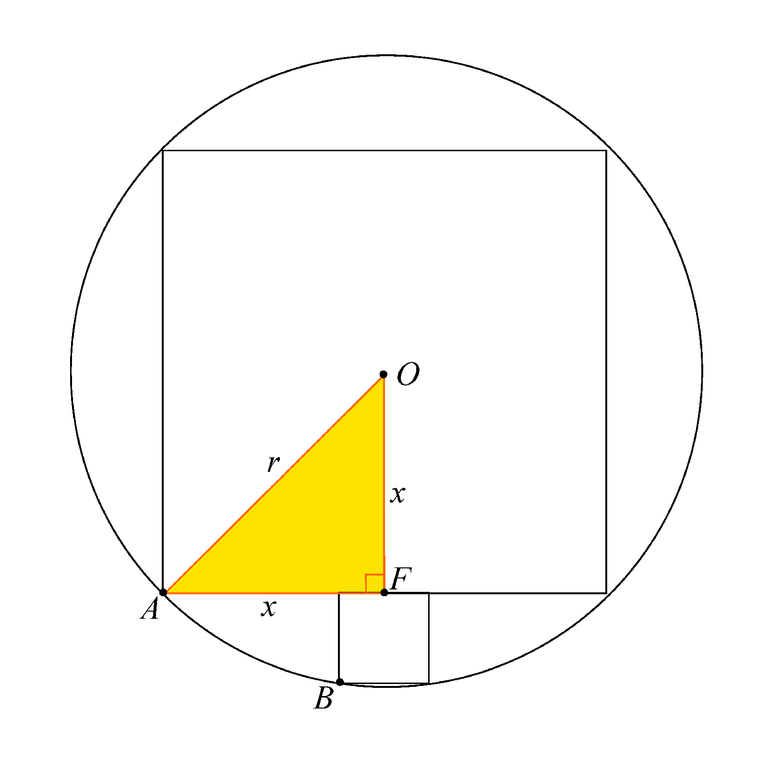
From symmetry, we can figure out that angle OAF is 45 degrees and/or that OF = AF = x (say). From our earlier definition, we have OA = r. Since we have a right-angled triangle OFC (coloured in orange), we can apply Pythagoras' Theorem.
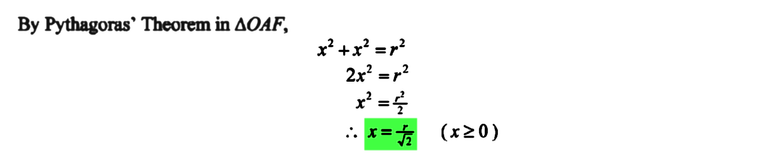
Solving that, we find that 
OK, we got part of the problem solved. Solving part of the problem is one of the heuristics recommended by Singapore's Ministry of Education for solving mathematical problem. Yes, but how do we solve the whole problem?
The Solution, Stage 2
We notice that two corners of the small square also just touche the circle. We label one of these corners as B. We can produce (extend) OF to touch the other side of the square at a point C (say). See the diagram below.
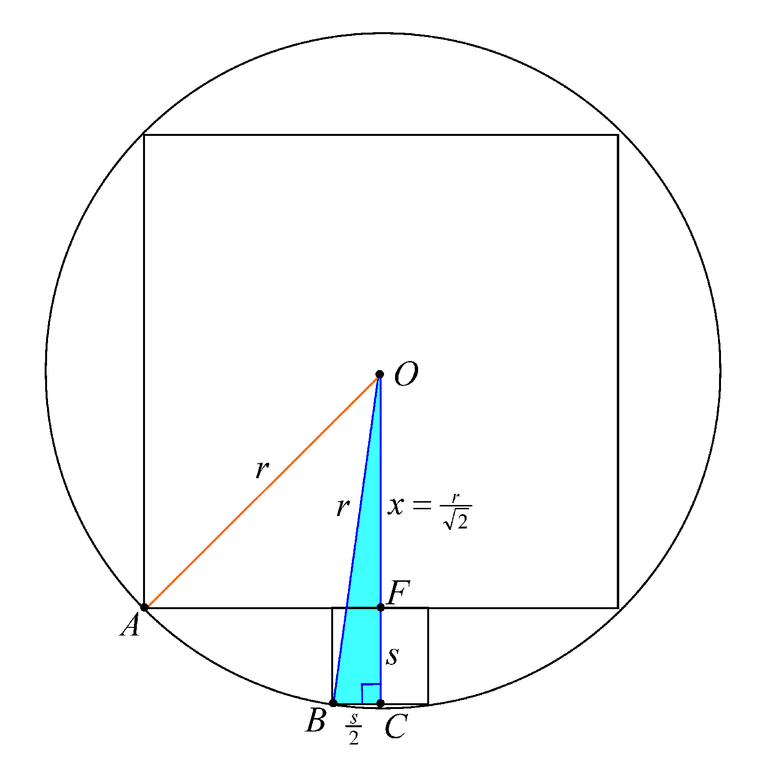
We know that OF = x = 
After 3 lines of manipulation, we arrive at an equation with r² and s². But since we want the ratio r / s, we divide through by s² and treat r / s as if it is one entity. Applying the quadratic formula, and rejecting the "minus" answer, we get 
Reflections
I have shown you the process of solving a challenging mathematical problem. What is needed to solve this problem successfully?
Solve part of the problem. e.g. I found x which is half of the length of the large square. This was useful later.
We need to make observations. e.g. that the corners of the large square and some corners of the small square touch the circle.
We need to translate the observations into mathematical equations. e.g. the use of Pythagoras' Theorem twice.
Note that we do not need to know the individual values of r and of s in order to solve for their ratio. By treating r/s as one thing, we make it unnecessary to solve them individually, which would be impossible anyway. Why impossible? That is because it is possible to have the same situation with an enlarged or shrunken diagram and thus have different values of r and of s. However, the ratio r/s will be the same, because we would solve the same quadratic equation and get the same answer.
Remember to keep cool and calm. If your brain is too excited, the signals in your brain get jammed, and you would not be able to think clearly, or get in touch with your intuition. However, some relaxation (but not too much) helps to keep your mind at an optimal state.
I hope you have learned something from this article.
Copyright
All the images in this article are my own original work.
Announcements
You might also want to read my recent articles:
"Singapore Math" : The Cows and Goats Problem
Inequality: Always, sometimes or never?
If you find my articles useful or interesting, please upvote and resteem them! Thanks !
Cheers!!!
@tradersharpe
-- promoting sharp minds
img credz: pixabay.com
Nice, you got a 3.0% @minnowbooster upgoat, thanks to @tradersharpe
Want a boost? Minnowbooster's got your back!
The @OriginalWorks bot has determined this post by @tradersharpe to be original material and upvoted(2%) it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
This was written very well! Before reading it I was going to sit down and do the problem but as soon as I read the actual problem I realized I had already completed it and knew the answer (bonus question in class). I hope to read more good content from you!
Hey @tradersharpe,
this is the first one I read before I figured it out by myself, shame on me :D
But unfortunetly I had nothing to draw. Neither pen and paper nor my pc.
But I had fun reading you answer too, thank you for your nice, educating math task :-)
Wow! very complex problem bro think think :)
It’s not that much easy @tradersharpe
Complex one..
Haha it's been a long time I've seen a geometrical problem :)
This post has received a 2.31 % upvote from @booster thanks to: @tradersharpe.