Hello friends of Steemit!
In this opportunity a powerful mathematical tool widely used in the analysis of electrical networks and control systems is analyzed, that has allowed the significant simplification in the analysis and solution of differential equations, which define the behavior of a great variety of physical systems.
Laplace Transform
Figure 1 - Biography of Pierre-Simon Laplace(1749-1827)
Image source
The bilateral Laplace Transform defined by Equation (1) has been very useful because of the mathematical simplicity that it represents when time signals are transferred to the domain of the complex frequency.
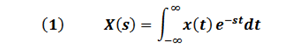
Where:
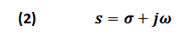
s → Complex frequency
σ → Frequency in Neper / second
ω → Frequency in radians / second
Since in practice the signals used are of the causal type (they exist for t> 0) the Laplace Transform given by equation (1) is expressed in the form:
The Laplace transform must comply with the condition:
Symbolically the Laplace transform is written in the form:
The change of domain (Frequency → time) of the signal is reversed once the system solution is found, for this purpose the Laplace inverse Transform is used, which is obtained through Equation (5):
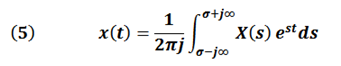
The inverse transform is written symbolically of the form:
The Laplace transform in two directions called transformed pair is expressed as:
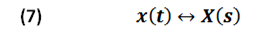
Table 1 and 2 show the transformed pairs of basic functions and the properties of the most relevant Laplace transform.
Table 1
Image source
Table 2
Image Source
Applications
In the model shown in figure x, the fundamental objective of the Laplace transform is illustrated. The system characterized by the transfer function H(s) determines the response of said system to a certain input and on which the output of the same depends. The input signal x(t), the system response h(t) and system output y(t), are converted to the frequency domain where in addition to obtaining the system bandwidth, the resulting equations are of algebraic character so its manipulation simplifies and facilitates the analysis in this domain.
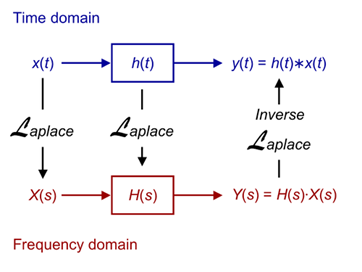Figure 2
Image source
In Figure 3 you can see an example of the natural response of an RC circuit. The circuit is converted to frequency through a Laplace transform where after obtaining the solution, the resulting equation is subsequently subjected to an inverse transformation shown in tables 1 and 2.
Figure 3
Image source
The filtering of signals is another valuable contribution that the Laplace Transform allows us to analyze and which is obtained from the transfer function, as shown in the following example.
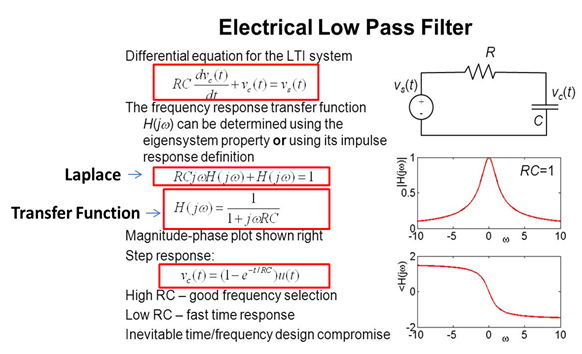Figure 4
Image source
The applications of the Laplace transform are not limited to electrical systems, their application extends to mechanical systems (see figure 5) and control systems in general.
Figure 5
Image source
In this way it is evident that the Laplace Transform is a method that allows a simplified analysis of systems governed by differential equations whose solutions by traditional methods are of high mathematical complexity.
References
Análisis de circuitos en ingeniería. William H. Hayt, Jr., Jack E. Kemmerly, Steven M. Durbin. Sexta edicion
Automatic Control Systems. Farid Golnaraghi, Benjamin C. Kuo. Ninth edition.
Circuitos eléctricos. James W. Nilsson, Susan A. Riedel. 7ª. Edition. Pearson Prentice Hall.
Digital Signal Processing using MATLAB. Vinay K. Ingle, John G. Proakis. Third edition.
Fundamentals of Physics. Halliday & Resnick. Jearl Walker.10th. Edition. Wiley editorial.
Señales y sistemas - Análisis mediante métodos de transformada y MATLAB. M.J. Roberts. Mc Graw Hill.
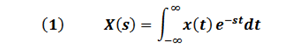
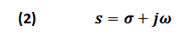
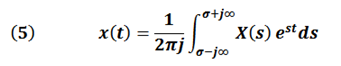
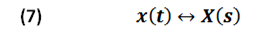
Congratulations @wilians! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness and get one more award and increased upvotes!
Congratulations @wilians! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Congratulations @wilians! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
Your next target is to reach 100 replies.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz: