The transmission of signals through transmission lines and waveguides has generated great advances and achievements in the scientific world and in the increasingly growing industry of telecommunications.
There are many variables involved that must be manipulated to achieve the final objective, which it's the transmission of signals quickly, cleanly and safely.
The transmission lines used as a means or channel to transport said signals to their target, which is denominated "load", must meet some requirements so that the maximum power of the signal is delivered to the load. This is only possible when the line and the load are coupled.
What is the Coupling?
When a signal travels in a medium that has a characteristic impedance, after impacting on a medium with a different impedance, part of it is reflected and another part is transmitted.
This is a basic principle of optics and electrodynamics based largely on the Snell Laws.
In such a way that the reflections generated in the border that separates the media is originated basically by the impedance changes (Line-load). This means that if there were no changes in the impedance, such reflections would be null. This ideal case is what is known in telecommunications as coupling and is the main condition that guarantees the maximum transfer of energy to the load.
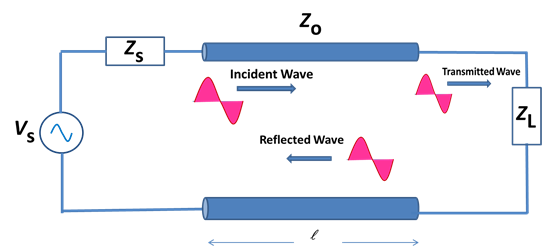
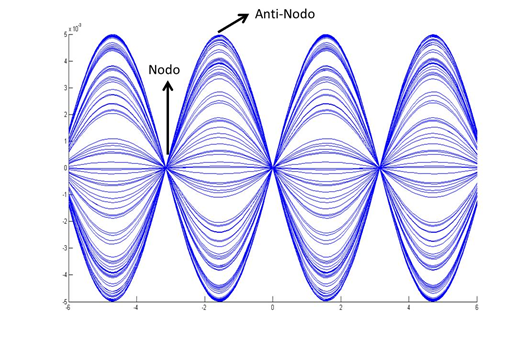
Figure 1 shows the incident and reflected voltage signals due to a decoupling between the transmission line and the load. The reflected and incident waves overlap to form a standing wave (see Figure 2).
This is a harmful effect to the transmission since the energy in a standing wave is confined between its nodes (zeros points of the wave) producing overvoltages in the line, in addition to reflected signals that are directed back to the source, producing damages to the generating equipment.
Author @wilians - Microsoft Powerpoint
VS ➝ Voltage in the Source
ZL ➝ Load Impedance
Z0 ➝ Impedance on the Line
Z S ➝ Impedance in the Source
 ➝ Line length
➝ Line length
Source
Since in practice there is no perfect coupling, one of the roles of a Telecommunications Engineer is to minimize the reflections in the load which are quantified through what is known as the Voltage Standing Wave Ratio (VSWR), which is a function of the reflection coefficient and is defined by Equation 1.
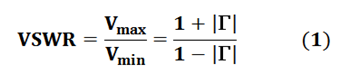
Vmax ➝ maximum voltage
Vmin ➝ minimum voltage
where:
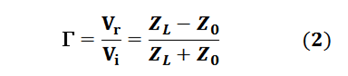
Vr ➝ Reflected voltage
Vi ➝ Incident voltage
The voltage values at any point on the line (z) and any time (t) are obtained from Equation 3.

The Voltage Standing Wave Ratio(VSWR) is a vital parameter in the analysis of transmission lines since it provides a measure of the degree of coupling between the line, the source and the load.
The following shows the extreme values of VSWR obtained from Equation 1.

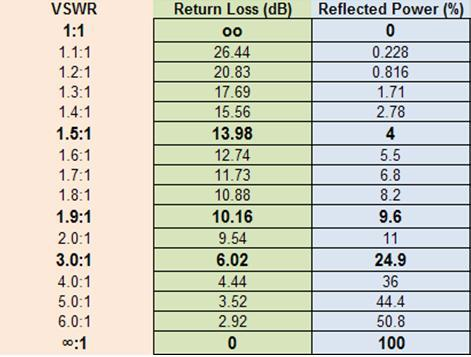
In Figure 3 some values of VSWR Versus the reflected power portentage are shown.
Source
In the field of work, measurement equipment is available to measure the standing wave ratio, see figure 4 and 5.

Source

Source
According to the values obtained from the Voltage Standing Wave Ratio (VSWR) in the transmission network, coupler circuits are used to guarantee an optimal transfer of the signal.
From the exposed analysis we can appreciate the importance of the associated variables in the transmission of signals.
The antennas used in small and large scale communication systems to transmit or receive signals must satisfy the coupling principles set here exposed. It is not a simple connection between a conductor and an antenna.
It is thanks to the compression of the phenomena of reflection and coupling conditions that it has been possible to advance to steps of giants in the local and global transmission networks.
References
Engineering Electromagnetics. Willian H. Hayt Jr., John A. Buck, Sixth Edition.
Field and Wave Electromagnetics. David K. Cheng. Second Edition.
Fundamentals of Applied Electromagnetics. Fifth Edition. FAWWAZT. ULABY.
Being A SteemStem Member