Hello friends of Steemit!
The electric field of some charge configurations is obtained in many cases through concepts or laws that evade the use of vector field analysis, due to the demands of mathematical analysis and the complexity that for many presents.
Gauss's law allows determining the electric field of distributions of discrete or continuous charge whenever they have a high degree of symmetry; otherwise its use ceases to be useful.
The electrostatic potential is another of the escape routes that allows determining the electric field of a charge distribution, making use of the fact that the electric field is the negative value of the gradient of the electric potential.
Since the electric potential is a scalar field, its obtaining at a point in space is translated into the simple addition of scalar potentials whose partial derivatives with respect to the present coordinates lead to the electric field at that point.
In this article I present a strictly vectorial method to determine the electric field resulting from an electric dipole.
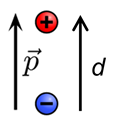
Source
The electric dipole is a configuration formed by a pair of opposite sign charges separated by a distance "d " and a dipole moment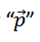 
which we will obtain in this development (see figure 1).
Source
The electric field of a point charge according to the coulomb law is given by:
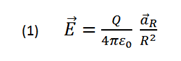
Q ➞ Electric charge (c)
ε0 ➞ Electrical permittivity constant of free space =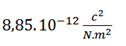 
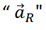is a unit vector in the direction of the vector 
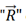directed from the point load to the point of analysis which is defined in the form:
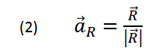abbreviating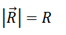 
Substituting (2) in (1) is obtained:
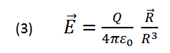
The resulting electric field at point P is given according to the principle of superposition by the vector sum of the fields of each of the electric charges that make up the Dipole.
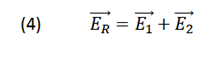
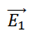➞ Electric field due to charge +q
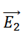➞ Electric field due to charge -q
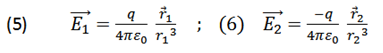
From the law of cosine you have:
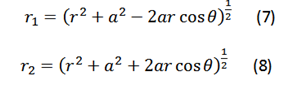
Vectorially:
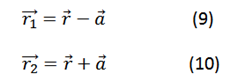
Substituting (5) and (6) in (4):
Substituting (7), (8), (9) and (10) in (11) and simplifying we obtain:
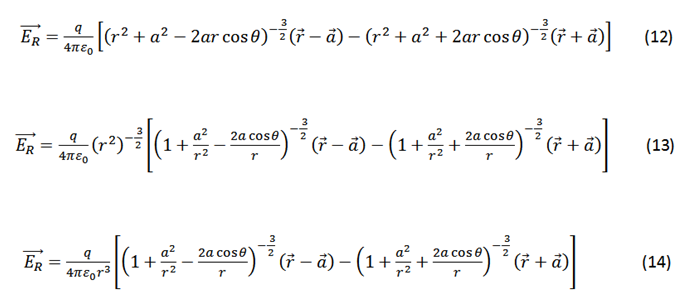
By binomial development:
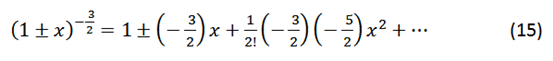
where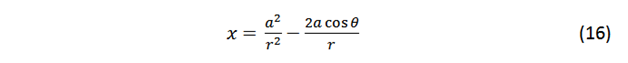 
Considering that a<<r the quadratic terms and higher order tend to zero.
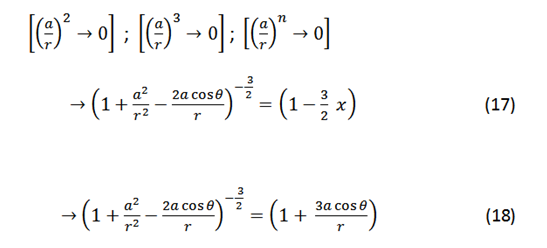
Applying (18) in (14) and simplifying:
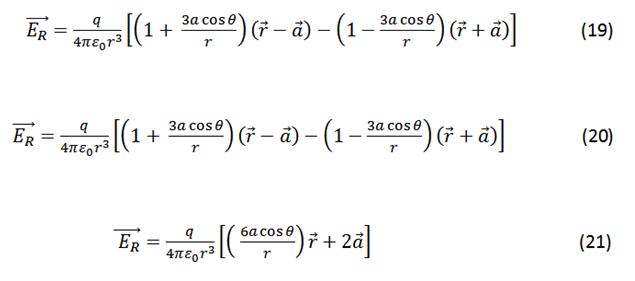
The vector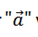 
and 
can be written in the same way
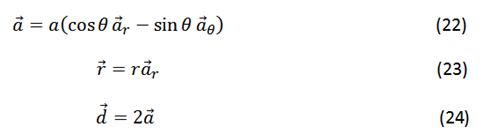
Substituting (22), (23) and (24) in (21) we have:
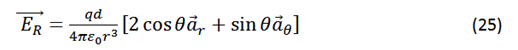
In the expression (25) we can observe the vector components 
of the electric field where the term "qd" is defined as the electrical dipole moment (see figure 1).
The development shown allows reinforcing the vectorial analysis, which is very useful in the calculation of electric, magnetic and gravitational fields.
References
http://laplace.us.es/wiki/index.php/Dipolo_el%C3%A9ctrico_(GIE)
Fundamental university physics. Vol.2: Fields and waves / Edward J. Finn, Marcelo Alonso
Physics for Science and Engineering / John P. McKelvey, Howard Grotch