En lógica analitica, los valores de verdad de una operación veritativa se pueden analizar de dos maneras, una de ellas es por medio de tablas de verdad, y la otra, a través de las demostraciones por vía de las leyes de las inferencias lógicas; hoy vamos a trabajar con las tablas de verdad, y para el próximo, iniciaremos con las demostraciones. Para lo cual vamos a definir el valor de verdad de cada operación veritativa en función de los valores de verdad de las proposiciones implicadas p y q .
In analytic logic, the truth values of a veritative operation can be analyzed in two ways, one of them is by means of truth tables, and the other, through the demonstrations by means of the laws of logical inferences; today we are going to work with the truth tables, and for the next one, we will start with the demonstrations. For which we will define the truth value of each truth operation in terms of the truth values of the propositions involved p and q.
We speak of the truth value of a veritative operation, we are referring to the truth value of the resulting proposition.
Comencemos con la conjunción ∧ / Let's start with the conjunction ∧.
In this case we wish to determine the truth value of the proposition p∧q, where p and q are any two propositions.
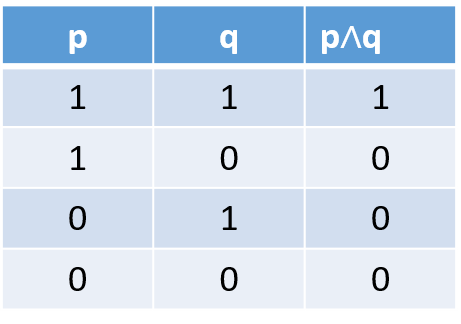
For this case, the proposition p∧q will be true if and only if both propositions are true, and it will be false if either one of the propositions p or q is false or both are false.
Construyamos la tabla de verdad para p∧q, donde el valor de verdad verdadero se designa por 1, y el falso, por 0./ Let us construct the truth table for p∧q, where the truth value true is designated by 1, and false, by 0.
Ejemplo
Sean las proposiciones p y q las siguientes:
p: Canadá está en Norteamérica
q: Caracas es la capital de Venezuela
Example
Let the propositions p and q be the following:
p: Canada is in North America
q: Caracas is the capital of Venezuela
Es claro que el valor lógico de p es 1 y también lo es el q, ambas proposiciones son verdaderas, por lo tanto, el valor lógico de p∧q también es 1, es decir, que es verdadera.
Is clear that the logical value of p is 1 and so is q, both propositions are true, therefore the logical value of p∧q is also 1, i.e., it is true.
Ella es:
Canadá está en Norteamérica y Caracas es la capital de Venezuela.
Veamos este otro ejemplo usando la proposición r=∼q (r es la negación de q), es decir que r: Caracas no es la capital de Venezuela. En este caso el valor lógico de r es 0 ya que es falsa, consecuentemente el valor lógico de p∧r es 0.
She is:
Canadá is in North America and Caracas is the capital of Venezuela.
Let's look at this other example using the proposition r=∼q (r is the negation of q), i.e. r: Caracas is not the capital of Venezuela. In this case the logical value of r is 0 since it is false, consequently the logical value of p∧r is 0.
A continuación vamos a colocar todas y cada una de las tablas correspondientes a cada una de loas operaciones veritativas restantes, luego pasaremos a la ejercitación en el próximo post. // Next we are going to place each and every one of the tables corresponding to each one of the remaining veritative operations, then we will move on to the exercise in the next post.
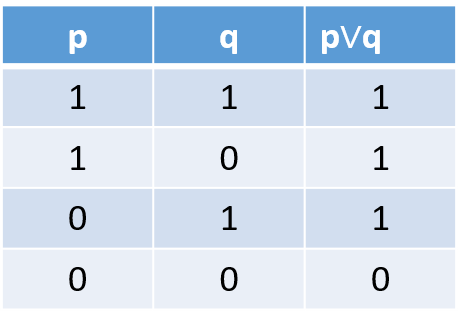
La disyunción p ∨ q
p ∨ q es verdadera si ambas proposiciones son verdaderas o solo una de ellas es verdadera, será falsa si ambas proposiciones son falsas./ p ∨ q is true if both propositions are true or only one of them is true, it will be false if both propositions are false.
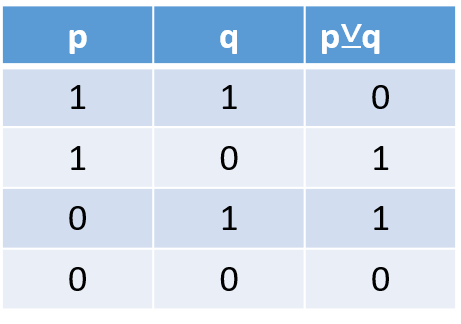
La disyunción exclusiva p ⊻ q
p ⊻ q es verdadera si los valores lógicos de p y q son diferentes, y será falsa si los valores lógicos de p y q son iguales./ p ⊻ q is true if the logical values of p and q are different, and will be false if the logical values of p and q are equal.
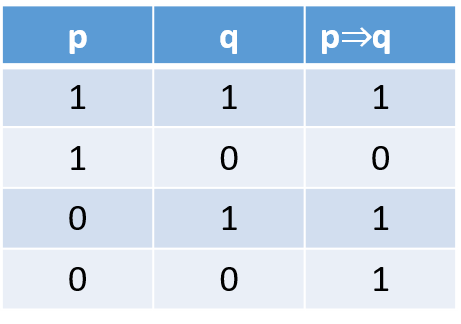
El condicional p ⇒ q // The conditional p ⇒ q
El condicional es falso cuando la proposición q es falsa, y será verdadero en los demás casos.// The conditional is false when proposition q is false, and will be true in all other cases.
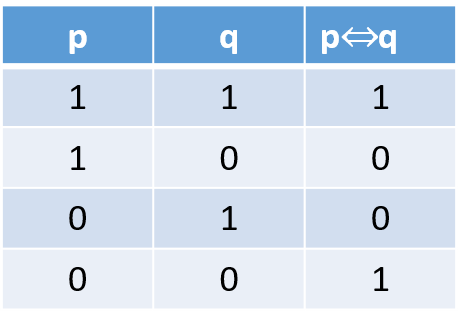
La equivalencia ⇔//The equivalence ⇔
La equivalencia o bicondicional será verdadero si los valores lógicos de p y q son iguales.// The equivalence or biconditional will be true if the logical values of p and q are equal.
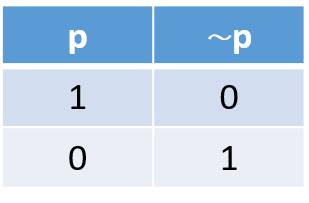
Y finalmente, la negación.// And finally, denial.

Congratulations @anmilnet! You received a personal badge!
You can view your badges on your board and compare yourself to others in the Ranking
Check out our last posts:
Support the HiveBuzz project. Vote for our proposal!