Aspectos básicos de la caída libre de un objeto

^{Caída libre.
Wiki LIC}

Cuando estudiaba en la universidad, vivía en el cuarto piso de un edificio de 10 plantas y solía lanzarles las llaves del apartamento a mis amigos que venían a estudiar. No tenía grandes dificultades porque en el 90% de los casos la podían atrapar en sus manos, el resto de las ocasiones caía al suelo con el temor que se partiera alguna llave. Sin embargo, en una oportunidad me pidieron algunas guías de laboratorio (unas 10 hojas con grapa) y las lancé de igual manera que las llaves, llevándome la gran sorpresa que esas hojas fueron a parar unos 10 metros del sitio donde estaba mi amigo. Las conjeturas comenzaron a aparecer, que si el roce, la velocidad del viento, el peso de las hojas, hasta hicimos un diagrama de cuerpo libre, para tratar de explicar lo sucedido.

Es una pequeña anécdota para entrar al tema de caída libre, cuando dejamos caer un objeto (como las llaves) desde cierta altura (como desde el cuarto piso) y podemos calcular varios parámetros: (a) la velocidad final (V_f) justo en el momento de llegar al suelo, también puede calcularse la velocidad en cualquier momento durante la caída. (b) el tiempo que tarda en llegar al piso, también el tiempo transcurrido en cualquier momento de su caída libre. (c) la altura desde la que se deja caer el objeto o la distancia que recorre a un tiempo determinado.

Para explicar este tema haré el planteamiento de un problema típico de Física y la caída libre. Suponiendo que estamos en la azotea del Edificio Marina City (ubicado en Chicago, Estados Unidos), emblemático por ser un conjunto residencial-comercial más alto del mundo. La altura desde el piso hasta la azotea son h = 179 metros, lugar donde se ubica una persona con una bola de billar, la de color verde (número 6), con una masa de 170 gramos, estira la mano y deja caer esa bola.

^{Edificio Marina City.
Diego Delso}

Lo más resaltante de un movimiento de caída libre es que el objeto se deja caer, por lo que su velocidad inicial, V_i = 0 m/s y como el movimiento es en la vertical hacia el piso, entonces se debe considerar la atracción de los objetos hacia el centro de la Tierra con una aceleración llamada gravedad (g = 10 m/s²), en muchos casos se usa este valor para facilitar los cálculos, pero el valor aceptado a nivel de la superficie terrestre es 9,80665 m/s².

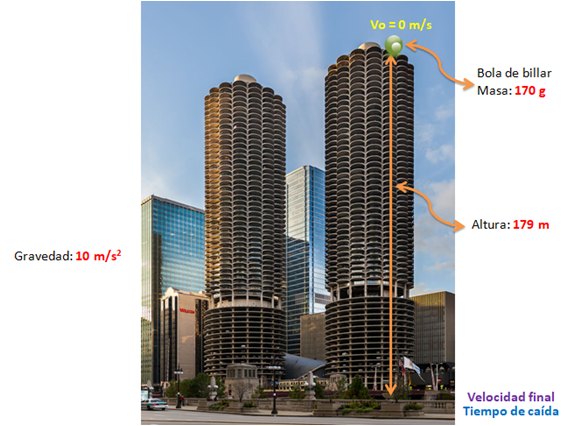
Las preguntas básicas para este tipo de movimiento son: (a) ¿cuál es la velocidad de la bola de billar justo en el momento de llegar al suelo? y (b) ¿cuánto tiempo tarda en llegar al piso?. Se debe calcular la velocidad final V_f y el tiempo de caida (t)

Aclaratoria: el color de la bola de billar y su masa no son datos relevantes para realizar los cálculos. Para hallar la velocidad final usaremos el valor de la altura del edificio y la aceleración de la gravedad (considerado como constante)

Usaremos los datos que disponemos:

Altura [m]	Aceleración g [m/s²]	Velocidad final [m/s]
179	10	?

Aplicaremos la primera ecuación presentada en la imagen anterior:

V_f = √ 2×(179 m)×(10 m/s²)

V_f = 59,8 m/s

Suponiendo que una persona se asoma a la ventana de su habitación ubicada en el piso 30, a 90 metros por debajo del punto de lanzamiento ubicado en la azotea, calcular la velocidad cuando la bola de billar pasa por el frente de esa persona.

Para diferenciar los cálculos que pueda realizar en cualquier tramo o punto de la trayectoria en caída libre, denominaré la velocidad en ese punto como V_p:

V_p = √ 2×(90 m)×(10 m/s²)

V_f = 42,4 m/s

Analizando este resultado, se esperaría que como la distancia en ese punto es la mitad de la altura del edificio, pues su velocidad debería ser la mitad de la velocidad final (V_f ≈ 60 m/s) que hemos calculado, es decir que se esperaban V_p ≈ 30 m/s.

La explicación es coherente con el movimiento acelerado, donde la velocidad se incrementa en el mismo valor cuando aumenta la unidad del tiempo.

Para calcular el tiempo de caída usaremos los datos que disponemos:

Altura [m]	Aceleración g [m/s²]	Tiempo de caída [s]
179	10	?

Como ya calculamos la velocidad final, podemos usar cualquiera de las 2 ecuaciones presentadas en la infografía anterior:

t = V_f/g = (59,8 m/s) / (10 m/s²) t = 5,98 s también:

t = √ 2×(179 m)/(10 m/s² t = 5,98 s

este resultado es lógicamente correcto, cualquiera de las ecuaciones son válidas para el movimiento en caída libre.

¿Cuánto tiempo ha transcurrido cuando haya recorrido los 90 metros de caída?

t = √ 2×(90 m)/(10 m/s² t = 4,24 s

Al transcurrir ese tiempo de caída podemos calcular la velocidad en ese punto específico, V_p = g.t = (10 m/s²)(4,24 s) = 42,4 m/s. Precisamente donde está ubicada la persona que observa desde la ventana del piso 30.

Para analizar otra situación, supongamos que en lugar de una bola de billar de 170 g, la persona deja caer un yunque de herrero cuya masa es de 50 kilogramos, ¿cuál será la velocidad final justo al llegar al piso y el tiempo de caída?

Aporte del Post

Cuando resolvemos los problemas de caída libre debemos tener en consideración que se trata de un movimiento acelerado (gravedad) y en una sola dirección (vertical y hacia abajo), no olvidemos que se deja caer con una velocidad inicial igual a cero, luego aplicamos las ecuaciones o fórmulas correspondientes al movimiento rectilíneo uniforme con aceleración constante y tendremos resuelto el problema planteado.

Texto original de @azulear

Si deseas profundizar tus conocimientos acerca de este tema, te recomiendo:

Sort:

Trending

[-]

stemsocial (63) 2 years ago

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!

Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).

You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.

$0.00