
Trayectoria parabólica.
Camera-man
| En el campo se utiliza un sistema de irrigación para suministrar agua a las plantaciones, por lo que se disponen tuberías de grueso calibre: 1, 2 o 3 pulgadas de diámetro. Los aspersores de bajo alcance cubren al menos un área de 9 metros por 9 metros, aunque en realidad su movimiento de rotación describe una circunferencia de 9 metros de diámetro. También se utilizan los difusores de agua con menor alcance, alrededor de 5 o 6 metros a la redonda, pero el detalle más relevante es que el agua describe una trayectoria parabólica desde el punto de partida hasta que cae en el terreno. |

Caudal en diferentes boquillas.
DMCA
Por observación directa del chorro de agua que sale de ambas boquillas se puede deducir que de la amarilla el caudal es de menor alcance, mientras que en la otra la boquilla es de menor área y se cubre mayor distancia para el riego, asociado a que el agua sale con mayor velocidad. Este es un ejemplo claro del fenómeno físico conocido como Efecto Venturi donde se relacionan varios parámetros: presión interna, área de sección transversal de un conducto tubular, velocidad del fluido y su densidad.

Caudal en tubo Venturi.
Thierry D.
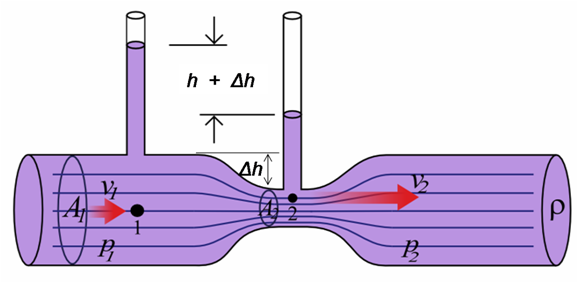
Parámetros efecto Venturi.
HappyApple
En el caso ideal, se tiene una manguera de agua de 1/2 pulgada, la cual tiene un diámetro interno de 13-15 mm, por la que circula un caudal de 35 litros cada minuto Caudal = 2,1 m3/h y que sale de la manguera con una velocidad determinada. Sin embargo, cuando se coloca el dedo en el extremo de la manguera o se adapta una boquilla de riego, entonces la velocidad de salida cambia instantáneamente. Esto sucede porque el área del conductor del fluido disminuye, y en consecuencia la presión es menor en esa sección, cumpliéndose el Efecto Venturi asociado con el Principio de Continuidad.
| Principio de Continuidad: establece que el caudal de un fluido se mantiene constante en una tubería cuando se estrecha el camino del fluido, es decir que se cumple la igualdad:
|
| En la figura que inserté arriba, se observa que en una tubería de sección transversal mayor A1, tendrá asociada una velocidad de flujo del fluido relativamente menor v1, en comparación con la sección de la tubería que se estrecha hasta un área de sección transversal menor A2 que provocará un aumento en la velocidad del fluido v2, cumpliendo el Principio de Continuidad. |
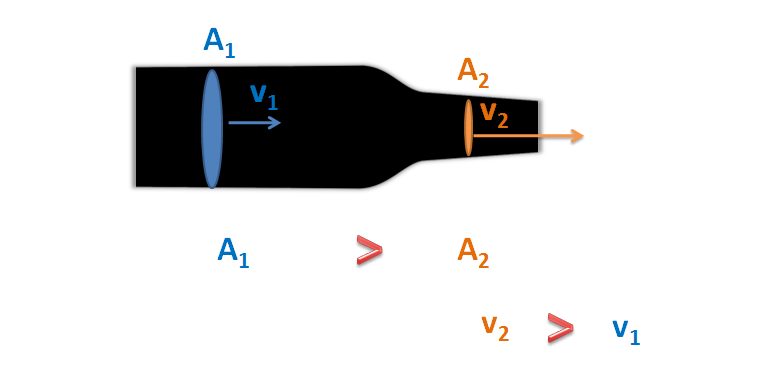
Principio de Continuidad
Usaremos esta imagen para plantear el ejemplo de la trayectoria parabólica de un chorro de agua que sale de la tubería con los siguientes valores:
| Ángulo del tubo | Velocidad del fluido | Diámetro de la boquilla |
|---|---|---|
| 45º | 5 m/s | 15 mm |
| 45º | 10 m/s | 6 mm |
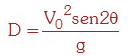


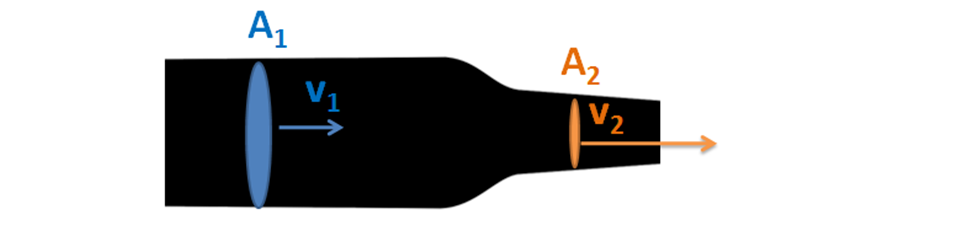
Si tenemos una tubería con un diámetro interno Φ = 15 mm, por la cual circula un caudal de agua de 1 m3/h (equivalente a ≈0,000278 m3/s), entonces podemos determinar la velocidad del flujo de agua:
|
Si tenemos esa misma tubería de diámetro interno Φ = 15 mm, pero colocamos una sección de menor diámetro interno Φ2 = 6 mm, por el Principio de Continuidad debe circular el mismo caudal de agua C2 = 1 m3/h, entonces podemos determinar la nueva velocidad del flujo de agua al colocar esta reducción tubular (boquilla):
v2 = C2/A2
A2 = πΦ2/4 = 28,21 mm2 = 0,00002821 m2
también: C1 = C2 = 0,000278 m3/s
v2 = (0,000278 m3/s)/(0,00002821 m2)
v2 = 9,86 m/s
Se comprueba que las relaciones entre el área de la tubería y la velocidad del flujo del fluido son inversamente proporcionales, mientras que el caudal se mantiene constante. ¿Qué sucede con la presión que ejerce el agua en las diferentes secciones?, en el siguiente post le comentaré lo relacionado con el Teorema de Bernoulli que relaciona estos parámetros de velocidad del flujo, la densidad del fluido, las presiones que acabo de mencionar y hasta la aceleración de la gravedad interviene en este teorema.
 Si deseas profundizar tus conocimientos acerca de este
tema, te recomiendo:
Si deseas profundizar tus conocimientos acerca de este
tema, te recomiendo:
Aporte del Post
Los conocimientos básicos sobre Física se pueden aplicar a situaciones reales y nos permiten resolver cualquier tipo de acontecimiento, por ejemplo el de determinar el alcance horizontal de un sistema de riego en un sembradío, usando 2 acontecimientos físicos como el movimiento parabólico y el efecto Venturi junto al Principio de continuidad para un caudal de fluidos. |
Texto original de @azulear

- Movimiento de un proyectil
- Movimiento parabólico
- Tiro parabólico
- Efecto Venturi
- Principio de Continuidad
- Caudal en tubería
- Dimensiones tuberías y caudal de agua
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.