Temas de Física: el péndulo simple y la dinámica circular

^{Oscilación del péndulo simple. Ruryk}

^{Dinámica del péndulo cónico. García S.N.}

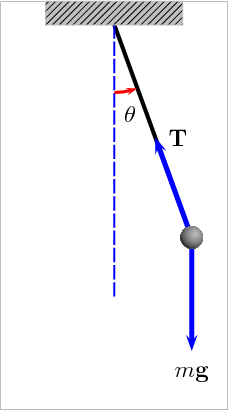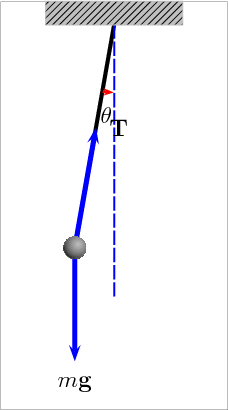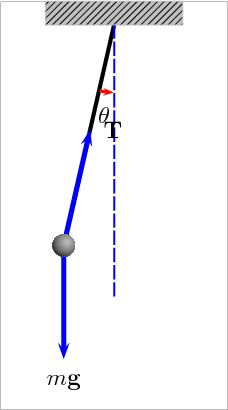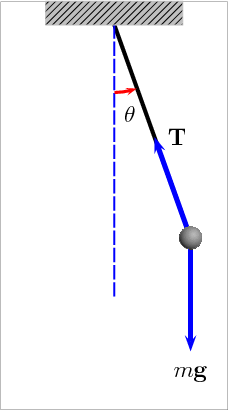
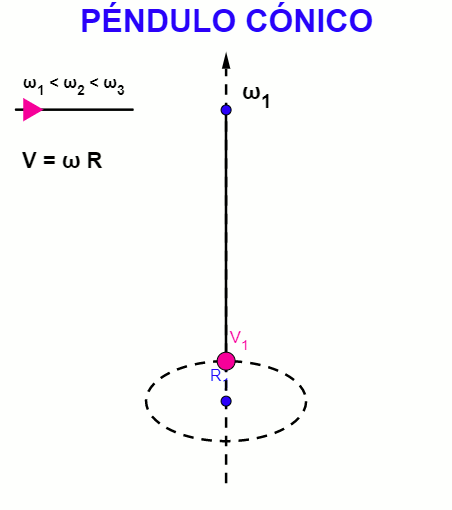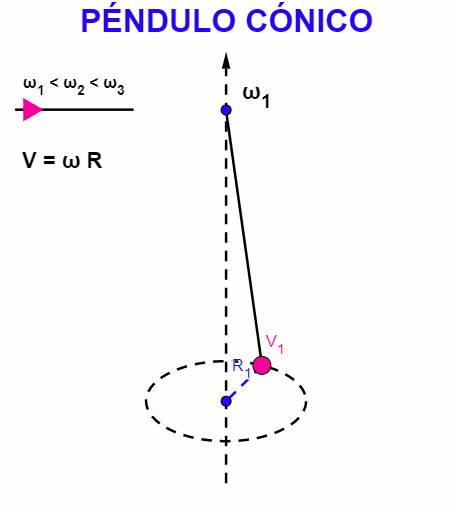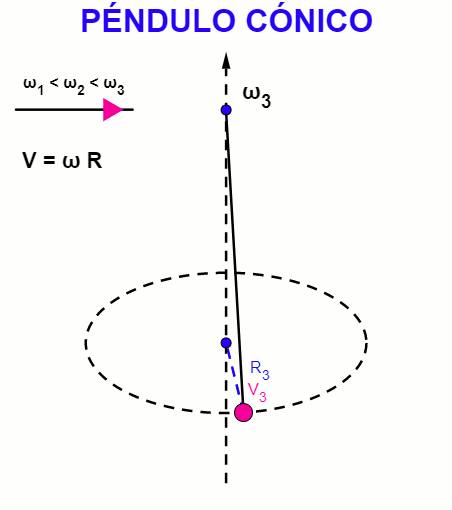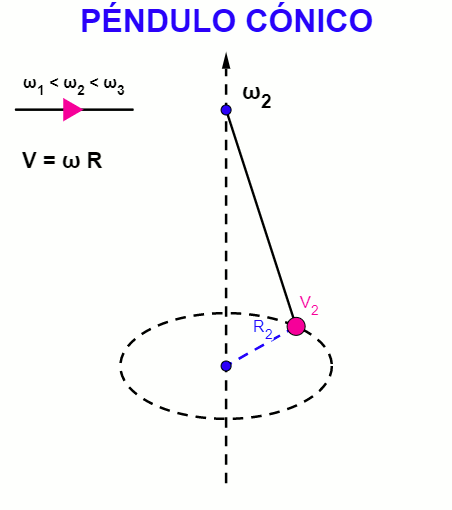
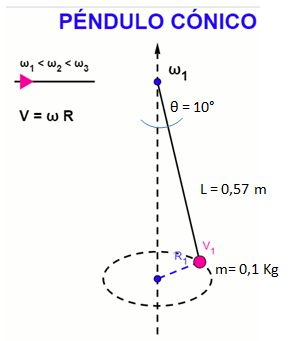
Uno de los experimentos más sencillos en la Física es tomar una cuerda y sujetarle en un extremo un objeto o masa. Son ejemplos clásicos: el péndulo simple, con un punto fijo superior y la masa que pende de esa cuerda se posiciona en un lugar que lo desplaza de su punto de equilibrio y comienza a oscilar en torno a ese punto, a la derecha e izquierda. El péndulo cónico también tiene un punto fijo superior y la masa se hace girar con una velocidad constante, describiendo una trayectoria circular de radio proporcional a esa velocidad.

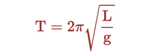
Ya sabemos que el experimento del péndulo simple es utilizado para determinar el valor de la aceleración de la gravedad de un lugar geográfico en específico, ya que el tiempo que tarda en hacer una oscilación completa o período "T", depende de la longitud de la cuerda "L", pero también del valor de la aceleración debido a la gravedad "g" del lugar, así:

^{Período de oscilación [s]}

despejando, podemos encontrar una ecuación para la longitud del péndulo.

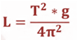
^{Longitud de la cuerda [m]}

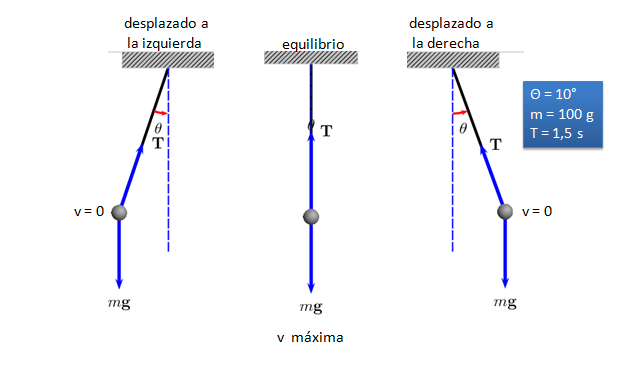
Cuando el ángulo de desplazamiento "θ" es pequeño, entonces la dinámica del movimiento se aproxima demasiado a un movimiento armónico simple m.a.s. que consta de una fuerza restauradora "F_R", como en la Ley de Hooke (F_R = -kX). Se deben considerar los casos excepcionales que no existe roce sobre la masa y que el ángulo de desplazamiento de su centro de equilibrio es muy pequeño.

La F_R en el péndulo simple es la que tiende a llevar a la masa a su posición de equilibrio y está representada como F_R = -m*g*senθ, pero como θ tiene un valor muy pequeño en radianes, entonces senθ≃θ , según la simplificación por aproximación considerando ángulos pequeños.

Si se requiere determinar la longitud de la cuerda del péndulo simple, podemos usar la ecuación presentada anteriormente, ya que se puede demostrar que este tipo de movimiento oscilatorio constituye un caso particular del m.a.s.


T = 1,5 s;
m = 100 g;
theta = 10°;
g = 10 m/s2;
L = ?

L = (1,5 s)².(10 m/s² )/4.(3,1415)²

L = 0,57 m

La longitud de la cuerda es algo más de medio metro de longitud, una medida razonable suponiendo un valor de g = 10 m/s² para facilitar los cálculos.

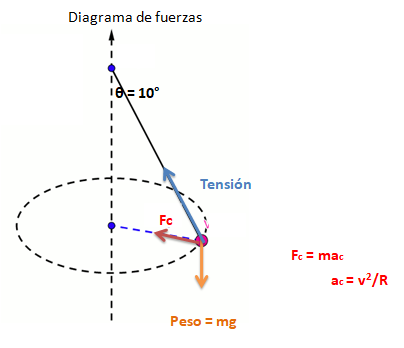
Como se trata de un objeto en movimiento, la sumatoria de todas las fuerzas no se anulan entre sí, es decir que existe una aceleración y velocidad que cambia con el tiempo, están relacionados con el ángulo de desplazamiento θ, así que ¿cuál es el valor de la aceleración y velocidad máxima, así como su frecuencia angular?

La frecuencia angular, que es una medida de la velocidad de rotación, según las ecuaciones del m.a.s., está dada por:

ω = √ (g/L)

^{Frecuencia angular [rad/s]}

Estamos suponiendo que este ejemplo trata un m.a.s., por lo que podemos usar las ecuaciones sin ambigüedades, de tal manera que la frecuencia angular es ω = 2*π*f, donde f es la frecuencia (correspondiente al inverso del período de oscilación (T), f = 1/T. Sustituyendo T = 2*π*√ (L/g), podemos calcular la frecuencia angular:

ángulo de oscilación	masa del péndulo	longitud de la cuerda
10°	100 g	0,57 m

la velocidad angular se calcula así:

ω = 2π/T ω = 2*(3,1415)/1,5s ω = 4,19 rad/s

también:

ω = √ (g/L) ω = √ (10 m/s²/0,57 m) ω = 4,19 rad/s

La velocidad en los puntos extremos a la derecha e izquierda del movimiento de vaivén del péndulo es igual a cero, mientras que en el punto de equilibrio, su velocidad será la máxima. Lo opuesto sucede con los valores de la aceleración, siendo máxima en los puntos extremos y cero en la posición de equilibrio, lo mismo le sucede a los valores de la fuerza restauradora.

La ecuación para calcular la velocidad en el punto de equilibrio, correspondiente a la velocidad máxima (v_máxima) es igual a:

v_máxima = ω*A

A es la amplitud o distancia horizontal que alcanza el péndulo simple en su movimiento oscilatorio. Los refiero a la siguiente imagen:

La amplitud A, corresponde al lado opuesto al ángulo de oscilación, visto en el siguiente triángulo:

A = (0,57 m)*Seno(10°) A = 0,099 m

la velocidad máxima es calculada a partir de los datos iniciales y los parámetros calculados. v_máxima = ω*A

v_máxima = 4,19 rad/s*0,099 m

v_máxima = 0,41 m/s

mientras que la aceleración (a_máxima) está dada por el cuadrado de la velocidad dividida entre la amplitud.

a_máxima = (v_máxima)²/A = (ω*A)²/A = ω²*A

a_máxima = (4,19 rad/s)²*0,099 m

a_máxima = 1,74 m/s²

Ahora lo que haremos es poner en movimiento circular a esta masa que pende de la cuerda, haciéndolo girar a una rapidez constante y que será el parámetro a calcular. Para este ejemplo, la longitud de la cuerda L = 0,57 m, el ángulo de rotación θ = 10°, la masa del objeto m = 100 g, la aceleración de la gravedad será tomada como g = 10 m/s²

El radio de la circunferencia descrita en el plano horizontal se calcula a partir del triángulo indicado en la figura.

R₁ = 0,57 m*Seno(10°) R₁ = 0,099 m

La dinámica del movimiento circular nos permite plantear el diagrama de cuerpo libre para identificar las fuerzas que intervienen en el movimiento circular:

por trigonometría,

tangente(10°) = F_c/Peso = ma_c/mg = v²/Rg =

de tal manera que la velocidad de rotación se calcula así:

v₁ = √(R₁*g*tangente(10°))

v₁ = √((0,099 m)*(10 m/s²)(0,1763)

v₁ = 0,42 m/s

La velocidad y la aceleración que adquiere esta partícula son debidas a la acción de diversas fuerzas que no se anulan del todo, proporcionando un movimiento oscilatorio y existiendo una fuerza restauradora en algunos casos.

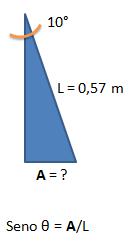
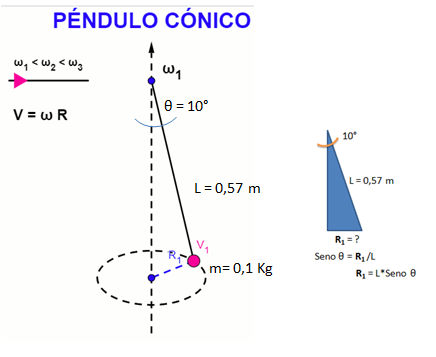
Como en los 2 ejemplos que he presentado se ha utilizado una masa sujeta por una cuerda y describiendo una trayectoria relacionada con una circunferencia, dejaré la interrogante acerca de si el lanzamiento de martillo es otro caso especial del movimiento armónico simple o de péndulo.

^{Lanzamiento de martillo. C0}

Aporte del Post

El péndulo simple realiza un movimiento de vaivén, describiendo un arco de circunferencia en el plano vertical, mientras que el movimiento de un péndulo cónico describe una circunferencia en el plano horizontal, siendo ejemplos particulares del movimiento armónico simple.

Texto original de @azulear

Si deseas profundizar tus conocimientos acerca de este tema, te recomiendo:

Has sido votado por

PROYECTO ENLACE

'Conectando Ideas y Comunidades'

PROYECTO ENLACE es un proyecto de curación de habla hispana enfocado en recompensar contenido de calidad y apoyar autores en su proceso de crecimiento en HIVE.

Creemos y apostamos por el futuro de esta gran plataforma, y estamos muy emocionados de poder hacerla crecer junto a esta comunidad. Así que te invitamos a publicar en nuestra COMUNIDAD y estar atento a todas las actividades que tenemos preparadas y que estaremos publicando en breve.

¿QUIERES AUTOMATIZAR TUS GANANCIAS DE CURACIÓN? SE PARTE DEL PROYECTO ENLACE APOYANDO A NUESTRO TRAIL EN HIVE.VOTE INGRESA AQUÍ PARA CONOCER LOS DETALLES.

¿QUIERES INVERTIR ENLACE? DESCUBRE COMO HACERLO Y GENERAR INGRESOS DE FORMA SEMANAL MEDIANTE TU DELEGACIÓN DE HP AQUÍ TE EXPLICAMOS COMO.

Te invitamos a participar en nuestro servidor de Discord: https://discord.gg/3S9y7BbWfS

Atentamente

EQUIPO ENLACE 2023

Sort:

Trending

[-]

hivebuzz (74) 2 years ago

Congratulations @azulear! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)

You received more than 45000 upvotes.
Your next target is to reach 50000 upvotes.

_{You can view your badges on your board and compare yourself to others in the Ranking}
_{If you no longer want to receive notifications, reply to this comment with the word STOP}

Check out our last posts:

	Our Hive Power Delegations to the March PUM Winners
	The Hive Gamification Proposal

Support the HiveBuzz project. Vote for our proposal!

$0.00

enlace (63) 2 years ago

stemsocial (63) 2 years ago

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!

Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).

You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.