Estuve el fin de semana en un parque del pueblo paseando a mi perro y respirando aire fresco, cuando me quedé mirando a dos niños jugando en el "sube y baja" y el más grande y pesado mantenía al otro niño "en el aire". Un entretenimiento infantil que consiste de una barra metálica alargada y sostenida en su punto central por una base metálica que le sirve de apoyo, mientras que en sus extremos se les coloca una especie de asiento y una pieza metálica para que los niños se sujeten y no caigan al suelo.
Balancín en el juego "sube y baja", Crédito: maxpixel (CC0)

Desbalance del centro de masas con el mismo punto de apoyo, Créditos: maxpixel (CC0)

Las 6 cajas están vacías, la caja a la derecha contiene un yunque de acero, maxpixel (CC0)
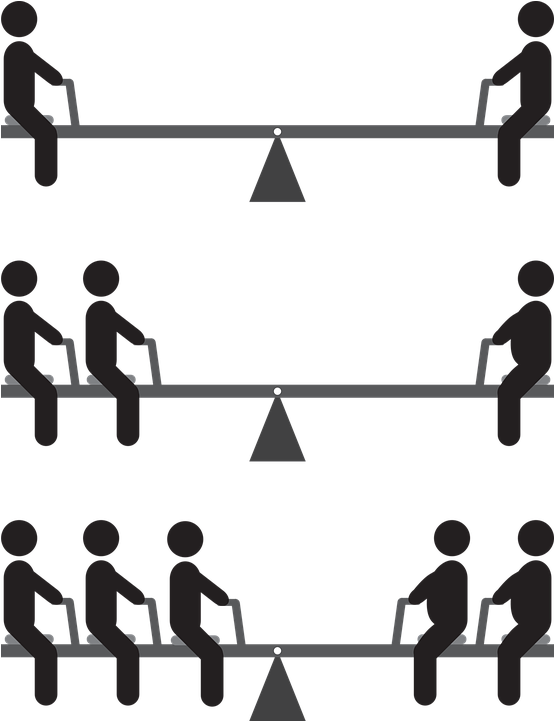
Conservación del punto de equilibrio y del centro de masas, Créditos: maxpixel (CC0)
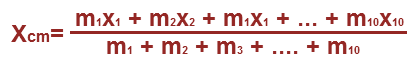
Para entender la figura donde los niños se ubican en los extremos del sube y baja, el punto de apoyo es una base fija y lo que se quiere es que el sistema se mantenga en equilibrio, es decir, una inmovilidad generada por la fuerza gravitatoria que actúa en sentido opuestos con referencia a este punto de apoyo. En el primer caso, cada niño de 5 años tienen la misma estatura, la misma masa corporal de 10 Kg y están ubicados a 5 metros de distancia del punto de sustentación del sistema (coloqué esta distancia grande porque luego ocuparé esa separación con más niños). Para utilizar la ecuación mostrada arriba, m1 = 10 Kg y a la izquierda sería x1 = -5 m, el niño a la derecha sería x2 = 5 m y m2 = 10 Kg, por lo que su centro de masa Xcm = 0 m, se ubica en el punto de sustentación y se mantendría en equilibrio. Recuerden que para que los niños se diviertan con su juego del sube y baja, estos deberán dar un impulso con sus piernas para sacar del equilibrio al sistema. Ahora se colocan 2 niños de 10 Kg cada uno del lado derecho, con x1 = -5 m y x2 = -4 m, mientras que del lado izquierdo se sienta un niño de la misma estatura, pero con una masa corporal de 18 Kg en el extremo derecho x3 = 5 m. Nuevamente, el centro de masa Xcm = 0 m, se ubica en el punto se apoyo y se debe mantener el equilibrio. Como dice mi profesor de Física, el tercer caso lo dejamos planteado como tarea para la casa y ustedes me dirán las ubicaciones de los 5 niños para que se mantenga el punto de equilibrio en la base del balancín.Aporte del Post
Texto original de @azulear
 Si deseas profundizar tus conocimientos acerca de este
Si deseas profundizar tus conocimientos acerca de este
tema, te recomiendo:
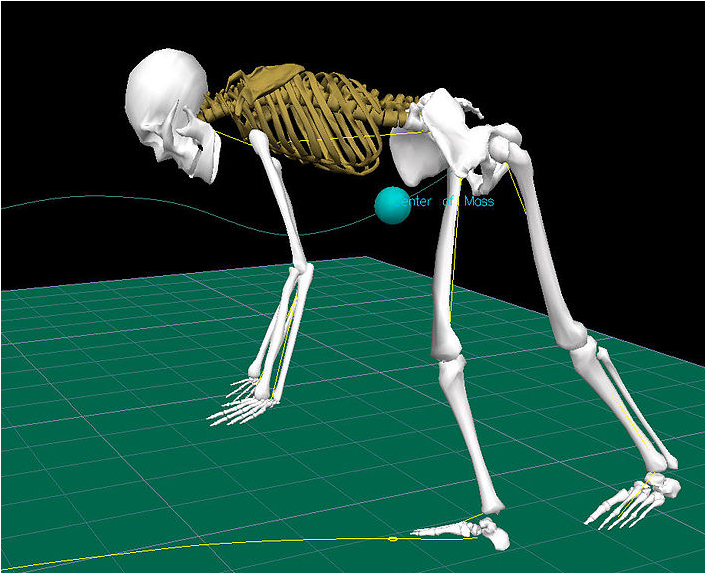
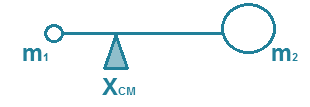
Centro de masa, Créditos: D. Gordon E. Robertson

Equilibrio y centro de masas
En este ejemplo, vemos que el punto de apoyo puede dar origen a un punto de equilibrio si las dimensiones geométricas son similares hacia ambos extremos. Además, las proporciones de masas sean las mismas y que estén distribuidas de manera equidistantes, tanto hacia la derecha como hacia la izquierda del balancín. En el caso ideal, deberíamos llegar al parque de juegos infantiles y observar en todo momento al balancín en posición horizontal, pues la sumatoria de todas sus masas multiplicadas por la distancia en ambos lados del balancín dará como resultado que el centro de masas estará ubicado en el punto de apoyo de la barra metálica del balancín y como el campo gravitatorio se considera uniforme en este plano, entonces el centro de gravedad coincide también en este mismo punto.

No hay que ser un experto Físico para entender que cuando se coloca un cuerpo con mayor masa en uno de los extremos se crea un desbalance en el sistema inicial de equilibrio y el centro de masas se desplaza hacia la izquierda (caja más grande) y el cuerpo de la derecha subiría cierta altura. El punto de apoyo se mantiene, se pierde la referencia como punto de equilibrio y se genera una desproporción de peso (caja grande P = Mg) > (caja pequeña p = mg) que provoca un desplazamiento del centro de gravedad del sistema inicial.

Como en todo fenómeno físico es importante tener en cuenta el enunciado del problema a resolver, así en el caso anterior se mencionó que la caja grande era el cuerpo con mayor masa, mientras que en la leyenda de las imágenes anteriores se menciona que las 6 cajas de la izquierda están vacías, mientras que la caja ubicada a la derecha contiene un yunque de acero, a lo menos debe tener una masa de 50 Kg y las 6 cajas no llegan ni a los 10 Kg. Nuevamente, el tema aquí es la pérdida del equilibrio, donde el contrapeso debería ser proporcional en ambos lados de la balanza, pero como hay mayor concentración de masa (y de peso) del lado derecho entonces pasará el efecto que se observa en la figura y no es un error que se ha cometido, sino que las condiciones indicadas anteriormente señalan que la caja ubicada a la derecha contiene un objeto de mucha masa.

De manera intuitiva y lógica deseaba presentar este post, pero inevitablemente debo llegar al punto de presentar una relación matemática que nos permite calcular el centro de masas para un sistema de cuerpos que se distribuyen en el sistema geométrico presentado.

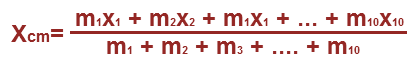
Para entender la figura donde los niños se ubican en los extremos del sube y baja, el punto de apoyo es una base fija y lo que se quiere es que el sistema se mantenga en equilibrio, es decir, una inmovilidad generada por la fuerza gravitatoria que actúa en sentido opuestos con referencia a este punto de apoyo. En el primer caso, cada niño de 5 años tienen la misma estatura, la misma masa corporal de 10 Kg y están ubicados a 5 metros de distancia del punto de sustentación del sistema (coloqué esta distancia grande porque luego ocuparé esa separación con más niños). Para utilizar la ecuación mostrada arriba, m1 = 10 Kg y a la izquierda sería x1 = -5 m, el niño a la derecha sería x2 = 5 m y m2 = 10 Kg, por lo que su centro de masa Xcm = 0 m, se ubica en el punto de sustentación y se mantendría en equilibrio. Recuerden que para que los niños se diviertan con su juego del sube y baja, estos deberán dar un impulso con sus piernas para sacar del equilibrio al sistema. Ahora se colocan 2 niños de 10 Kg cada uno del lado derecho, con x1 = -5 m y x2 = -4 m, mientras que del lado izquierdo se sienta un niño de la misma estatura, pero con una masa corporal de 18 Kg en el extremo derecho x3 = 5 m. Nuevamente, el centro de masa Xcm = 0 m, se ubica en el punto se apoyo y se debe mantener el equilibrio. Como dice mi profesor de Física, el tercer caso lo dejamos planteado como tarea para la casa y ustedes me dirán las ubicaciones de los 5 niños para que se mantenga el punto de equilibrio en la base del balancín.
Los temas de la Física actúan a diestra y siniestra, están en todos lados y en todo momento, sólo fui un día a pasear a mi perro y pude desglosar un tema de equilibrio y centro de masas en un sistema que estaba en movimiento y seguramente no estaba balanceado porque los niños no eran de la misma contextura ni tamaño.
Texto original de @azulear

tema, te recomiendo:
- Centro de gravedad
- Equilibrio y centro de masa
- Juego del sube y baja
- Centro de gravedad y punto de equilibrio
A veces la mitad de uno no es el ombligo

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.