Hola amantes de la ciencia en #steemstem y #stem-espanol.
Hoy les traigo un post referente a un tema particular que estudié mientras transitaba en mis experiencias del Laboratorio en la Universidad del Zulia. El tema consiste en un nuevo método para calcular la brecha de energía en cristales semiconductores.
Mediante la curva experimental del Coeficiente de absorción óptica en función de la Energía, obtenida a través de esta técnica, determinamos los puntos críticos y los empleamos para determinar el valor de dicha brecha de energía.
PUNTO CRÍTICO
Para definir al punto crítico es necesario antes conocer que es un punto de inflexión. En matemáticas, un punto de inflexión en un punto donde los valores de una función continua cambian de un tipo de concavidad a otra.
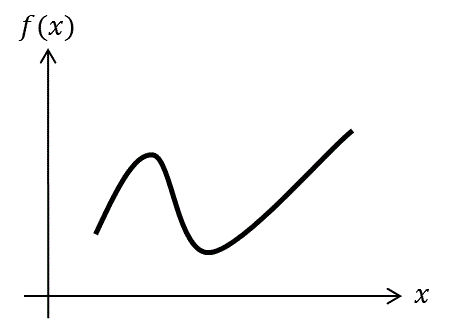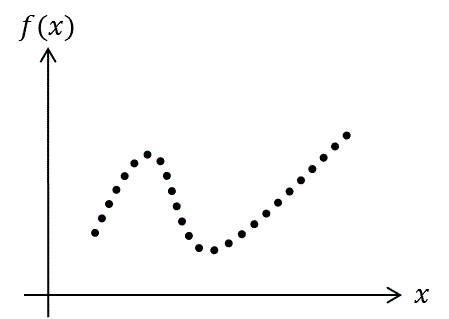
Figura 1. Puntos de una función continua | por @djredimi2
Una función continua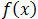 
es conocida como una curva característica representada en coordenadas ortogonales. Una curva, a su vez, es una sucesión de puntos (figura 1). La línea recta es un ejemplo de curva. Dicho de esta manera, definimos al punto de inflexión como un punto donde la curva de una función cambia de dirección. Una característica es que la segunda derivada en el punto de inflexión es cero (figura 2).
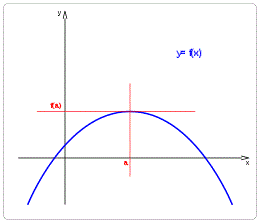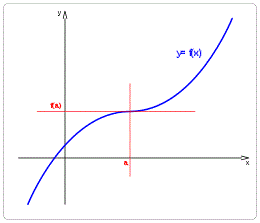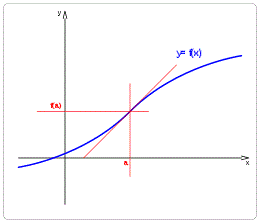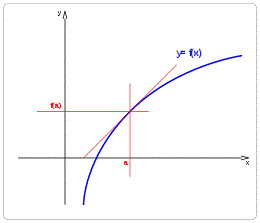
Figura 2. Punto de inflexión [a, f(a)] de algunas funciones | Todas las imágenes por Dnu72 en Wikipedia |
Animación por @djredimi2
Un Punto Crítico, por su parte, es cualquier punto dentro de la curva de la función donde dicha función no es diferenciable, es decir, su derivada es cero. Esto quiere decir, que la gráfica de la función en un punto crítico no admite una curva tangente, o su tangente es una recta horizontal o vertical. Si se cumplen las siguientes condiciones, un punto de inflexión es un punto crítico. Si las trazas de la función desde a hasta b es creciente y desde b hasta c es decreciente, la tangente es horizontal, la función es una superficie convexa y el extremo se conoce como un punto máximo (figura 3A). Y si las trazas de la función desde a hasta b es decreciente y desde b hasta c es creciente, la tangente también es horizontal, la función es una superficie cóncava y el extremo es un punto mínimo (figura 3B). Para ambos casos, el punto de inflexión [b, f(b)] es un punto crítico.
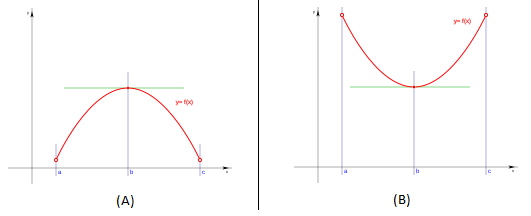
Figura 3. Punto crítico [b, f(b)]. (A) Punto máximo. (B) Punto mínimo | Imagen (A) y (B) por Dnu72 en Wikipedia |
Edición por @djredimi2
Análisis del coeficiente de absorción óptica.
El coeficiente de absorción óptica para cristales semiconductores ha sido descrito es post's anteriores, ver este post y este. En esta ocasión, se describirán los comportamientos de la derivada primera y segunda para el coeficiente de absorción óptica. De esta manera, el coeficiente de absorción óptica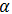 
es,
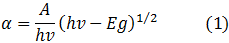
Donde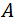 
es una constante que varía poco con la energía, 
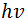es la energía del fotón incidente y 
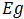es la brecha de energía.
Para conocer los puntos críticos de esta función procedemos a encontrar la primera derivada de la ecuación (1) con respecto a la variable independiente que es la energía de los fotones,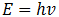 
. De esta manera:
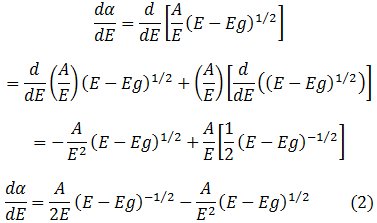
El punto crítico de la primera derivada se obtiene al igualar la ecuación (2) a cero. Para este caso se obtiene una singularidad, ya que al despejar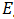 
para obtener el valor crítico, este resulta en una solución donde 
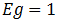, de manera que mediante la ecuación (1) no es posible determinar los puntos críticos (omití el análisis ya que no son relevantes para esta publicación).
Por lo que se procede a transformar la ecuación (1) en:
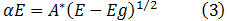
Y la primera derivada de la ecuación (3) es,
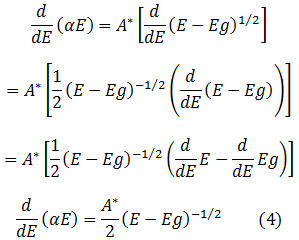
Mediante el cálculo anterior confirmamos que existe por lo menos un punto crítico en la ecuación (3). De esta manera procedemos a calcular el valor de dicho punto igualando la ecuación (4) a cero, es decir:
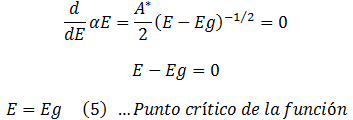
Este punto crítico a su vez se comporta como un punto de inflexión. Esto tiene dos argumentos puntuales:
- El comportamiento de la curva coeficiente de absorción óptica en función de la energía de los fotone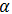s ( vs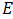
). Sabemos que la brecha de energía de un cristal semiconductor se define como el aumento brusco del coeficiente de absorción óptica en función de la energía. Este aumento, representa un cambio en la concavidad de la función y el punto donde empieza dicho cambio describe al punto de inflexión. (Ver sección Post recomendados). - El comportamiento de la derivada primera del coeficiente de absorción óptica según ecuaciones (4) y (5). Como fue explicado anteriormente, existe un punto crítico en dicha función que es igual a la brecha de energía.
Cálculo de Eg por el punto crítico del coeficiente de absorción óptica en CuInTe2
El compuesto ternario, CuInTe2 es un cristal semiconductor del cual se han realizado amplios estudios sobre sus propiedades estructurales, ópticas y eléctricas. El Dr. G. Marín @iamphysical es uno de los grandes científicos que ha estudiado esta muestra. En el post "¿Cómo determinar la brecha de energía en un semiconductor?" el Dr. nos proporcionó un valor de brecha de energía de 0,98 eV.
Hace aproximadamente 7 meses mostré mi cálculo propio de la brecha de energía de una muestra de CuInTe2. Los datos se obtuvieron por mi persona, bajo la tutoría del Dr. Marín, como experiencia de laboratorio. Se analizaron los datos empleando la extrapolación de la curva del coeficiente de absorción en función de la energía de los fotones (ver este post). Y resultó en un valor de brecha de energía de 1,00454 eV.
En este post se realizará un segundo análisis sobre la curva obtenida en mi experimentación. Esta es la curva de absorción de la figura 4.
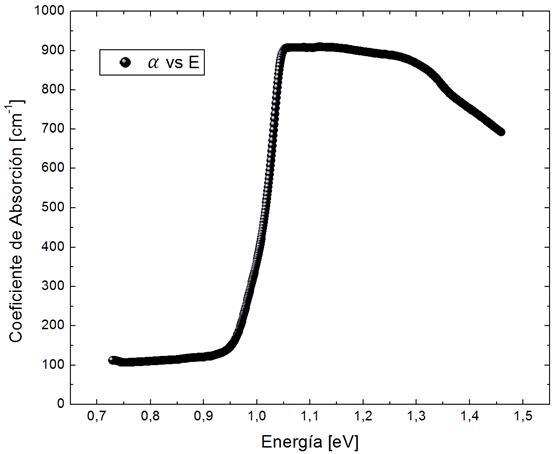
Figura 4. Coeficiente de absorción óptica en función de la energía de la muestra CuInTe2 |
por @djredimi2 con la ayuda del software OriginLab 6.1
Partiendo de estos datos experimentales se obtuvo la gráfica del producto entre el coeficiente de absorción óptica y la energía por la energía (figura 5).
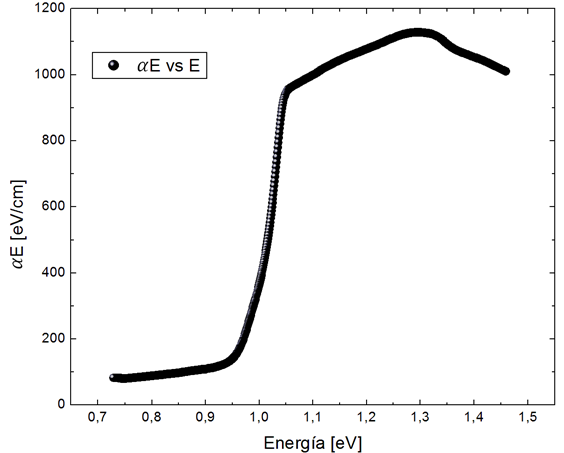
Figura 5. Producto del coeficiente de absorción óptica y la energía en función de la energía, de la muestra CuInTe2 |
por @djredimi2 con la ayuda del software OriginLab 6.1
Para ambos casos, figura 4 y figura 5, la curva presenta un aumento brusco de la pendiente, lo que significa la presencia de por lo menos un punto de inflexión. Sin embargo, es la derivada primera la que confirma la presencia de un punto crítico.
El software OriginLab 6.1, nos permite derivar una función empleando el comando "Differentiate", al acceder a la opción "Analysis - Calculus". Empleando la derivada de la figura 5 en el rango de energía desde 0,93 hasta 1,07 eV, obtenemos:
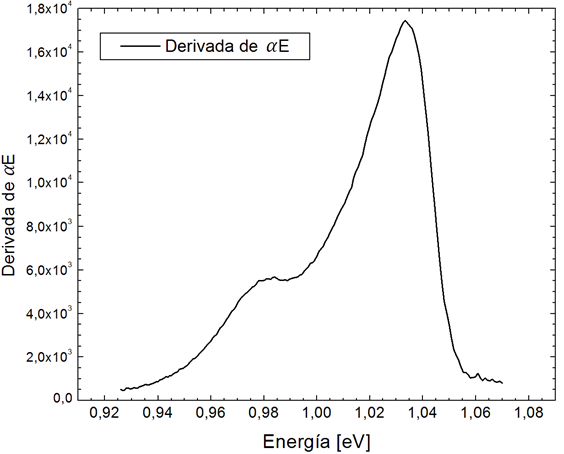
Figura 6. Derivada del coeficiente de absorción óptica por E en el rango 0,93 hasta 1,07 eV, de CuInTe2 |
por @djredimi2 con la ayuda del software OriginLab 6.1
En esta figura podemos visualizar dos superficies convexas que anuncian la presencia de dos puntos críticos. Sin embargo, un análisis sobre dichas profundo determina a quien pertenece dichas crestas.
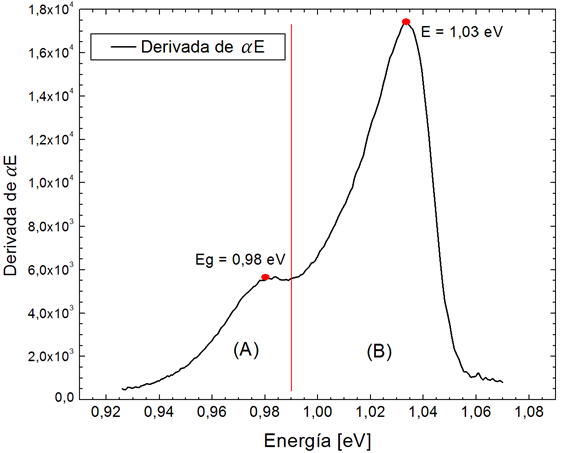
Figura 7. Análisis de la curva en la figura 6 | por @djredimi2 con la ayuda del software OriginLab 6.1
Si separamos la curva en dos partes (figura 7). El punto máximo de la curva en la parte B coincide con un punto de inflexión presente en la curva de intensidad incidente. Esto quiere decir que el punto máximo E = 1,03 eV coincide con un punto de inflexión de la curva característica del detector empleado en la experimentación (ver figura 8). Este punto no representa nada en la muestra CuInTe2.
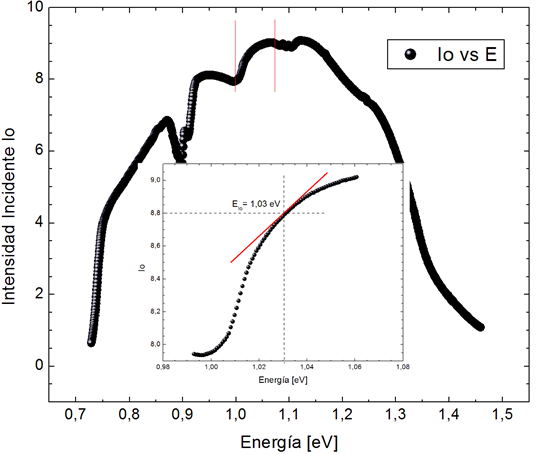
Figura 8. Demostración del punto de inflexión de 1,03 eV en la curva de intensidad incidente en función de la energía |
por @djredimi2 con la ayuda del software OriginLab 6.1
Por otro lado, en la parte A de la curva en la figura 7, el punto máximo coincide con el valor confirmado por el Dr. Marín. Este tiene como valor 0,98 eV y representa el valor de la brecha de energía del cristal semiconductor CuInTe2.
CONCLUSIÓN
El valor Eg = 0,98 eV para el compuesto CuInTe2 confirma la eficacia de este método. El punto crítico es entonces, un método eficaz para calcular la brecha de energía de cristales semiconductores mediante el coeficiente de absorción óptica.
Sin embargo, se recomienda emplear un método que se ajuste a la curva de la derivada según ecuación (4). Por ejemplo, se puede emplear un ajuste Lorentziano o Gaussiano para determinar el valor del pico máximo con mayor eficiencia.
Gracias mis estimados steem-lectores.
Att. Licenciado Daiver Juarez, @djredimi2.
POST RECOMENDADOS
- FÍSICA DEL ESTADO SÓLIDO: Introducción a los Semiconductores. TEMA CONVERSATORIO. Por @djredimi2.
- Caracterización óptica de nanocristales Semiconductores. Por @djredimi2.
- Monocromador Spectra-Pro 2750 para la caracterización óptica de Nanocristales Semiconductores. Por @djredimi2.
- ELIPSOMETRÍA ESPECTROSCÓPICA (SE). Propiedades ópticas del semiconductor CdTe. Por @djredimi2.
REFERENCIAS CONSULTADAS
- Bartle G. Robert. (2011). "Introduction to Real Analysis". Fourth Edition. University of Illinois, Urbana-Champaign. John Wiley & Sons, Inc.
- Stewart, James. (2008). "Cálculo de una variable. Trascendentes tempranas". Sexta edición. McMASTER UNIVERSITY. Traducido por Jorge Humberto Romo M.
- @iamphysical. "¿Cómo determinar la brecha de energía en un semiconductor?". Fuente.
Si estás interesado en unirte al grupo de Física, te invito cordialmente a chat oficial de #stem-espanol, registrándote en discordapp.com y accediendo a este enlace
Conoce todo sobre el logo visitando este enlace.
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks you my dear friend @steemstem
Importantísimo material para conocer la brecha energética de cualquier compuesto semiconductor, dato importante para futuras aplicaciones semiconductoras. Gracias por compartir tan genial contenido colega
Gracias por el comentario mi hermano.!
Hi @djredimi2!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thanks you my dear @utopian-io