Durante la travesía de la elección del Trabajo Especial de Grado (Tesis de pregrado), algunas veces pasamos por la selección y estudio de más de un proyecto. En mi caso, me tocó estudiar varios proyectos. Aunque, el área que más me emociona de la física es la física del estado sólido existe un gran multitud de ramas relacionadas al mismo. Una de estas ramas es el estudio de las Propiedades Ópticas de cristales semiconductores, como la constante dieléctrica compleja, el indice de refracción, el coeficiente de extinción y las relaciones de dispersión óptica.
Ya hace unos meses atrás les había presentado a la Elipsometría Espectroscópica, la cual es una de las técnicas experimentales que nos permite obtener estas propiedades ópticas. Este es el post "ELIPSOMETRÍA ESPECTROSCÓPICA (SE)".
Por lo tanto, esta viene a ser la segunda parte de dicho post, el cual esta relacionado con el análisis de los resultados a partir de las medidas experimentales de las propiedades ópticas de cristales semiconductores obtenidas por Elipsometría Espectroscópica.
Para la mejor comprensión del tema en cuestión debemos definir algunos conceptos.
¿Qué es la Estructura de Bandas?
Para la comprensión de la estructura de bandas de un cristal semiconductor es necesario acudir a su comportamiento atómico, es decir, a la naturaleza de sus enlaces y su distancia interatómica. Esto nos permite conocer el mecanismo físico de la conducción de electrones y huecos en semiconductores. Para ello entonces, estudiaremos la energía cuantizada de los electrones en función de la distancia interatómica en un semiconductor con estructura cristalina tipo diamante (figura 1).
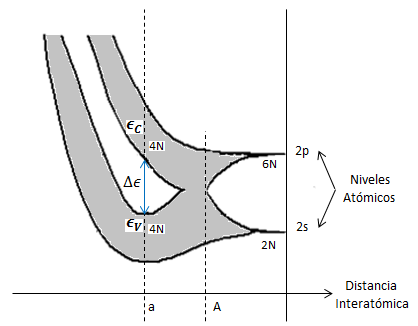
Figura 1. Las bandas de energía que se originan de los estados atómicos 2s y 2p de carbono cristalino como función de la distancia interatómica. Fuente de imagen base: Wikimedia, Edición: Lic. Daiver Juarez, @djredimi2
Para el caso del Carbono C que tiene configuración electrónica 1s22s22p2. Si combinamos N átomos aislados se forma un cristal, por lo tanto los niveles atómicos 2s (que se refiere a dos estados con electrones) y los 2p (que se refiere a seis estados con dos electrones y cuatro vacancias) se amplían formando bandas de energía. Esto ocurre cuando la distancia interatómica está en condiciones ambientales.
¿Pero qué pasa si la distancia interatómica disminuye?
Al disminuir la distancia entre átomos (por ejemplo, ejerciendo presión sobre la muestra de estudio), entonces dichas bandas se amplifican aún más y se superponen (Punto A de la figura 1). Si la distancia interatómica se hace aún más pequeña, observaremos de nuevo la aparición de nuevas bandas que ahora cuentan con 4N estados electrónicos que bastan para llenar ambas bandas. Cuando se alcanza a la distancia interatómica de equilibro “a”, estas bandas están separadas por una región de energías prohibidas, cuya anchura posee un valor característico de cada muestra. A la banda inferior se le conoce como la banda de valencia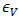 
y a la banda superior, banda de conducción 
.
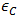Si lográramos seguir aumentando la distancia interatómica observaríamos toda una gama de bandas. A esto se le conoce como estructura de bandas. A la primera región de energías prohibidas, se le conoce como brecha de energía fundamental, o simplemente brecha de energía.
Estructura cristalina y Estructura de bandas.
La naturaleza periódica de la red cristalina es aprovechada por la estructura de bandas para el cálculo de la misma por medio del uso de la teoría de Bloch. Esta teoría establece que la energía propia de un electrón en un cristal se puede escribir como ondas de Bloch. En un potencial de la red periódica, la ecuación Schrödinger tiene como solución la función de onda Bloch:
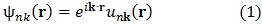
Donde,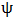 
es la onda de Bloch, 
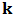es el vector de onda, 
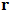es el vector posición, 
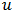es una función periódica y 
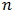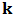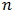es un índice discreto llamado también índice de banda. La ecuación nos dice que para cada valor de hay soluciones a la ecuación de Schrödinger, este 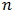simplifica el números de bandas de energía. Cada uno de estos cambia en función de 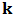formando bandas. Para cada banda se puede definir una función 
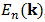, que es la relación de dispersión para los electrones de esa banda.
Entonces, podemos describir a la Zona de Brillouin de un cristal como un poliedro en el espacio vector de onda que se relaciona con la red cristalina. Los puntos espaciales dentro de la zona de Brillouin se denotan como Γ, Δ, Λ, Σ. Para visualizar la forma de una banda como una función del vector de onda se requiere de una gráfica en el espacio de cuatro dimensiones, de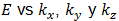 
. Por ejemplo para el Silicio monocristalino se observa una estructura de bandas (figura 2a) que coincide con una zona de Brillouin (Zincblenda) de una estructura cristalina cubica centrada en las caras FCC (figura 2b).
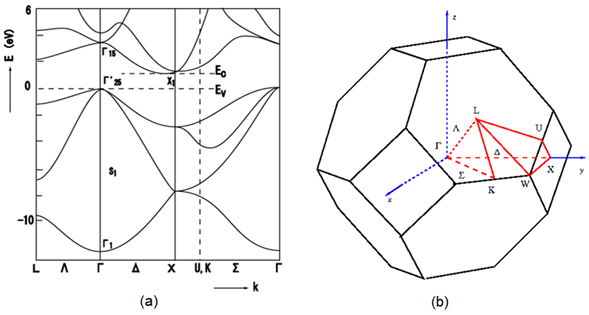
Figura 2. (a) Estructura de bandas del Silicio y su (b) Zona de Brillouin. Fuente de imágen base: Wikimedia, Edición: Lic. Daiver Juarez, @djredimi2.
Distribución de Cauchy-Lorentz.
La distribución de Cauchy-Lorentz, también conocida en física como la distribución de Lorentz y como la función Lorentziana, es una distribución de probabilidad estadística cuya función de densidad es:
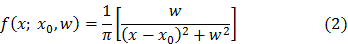
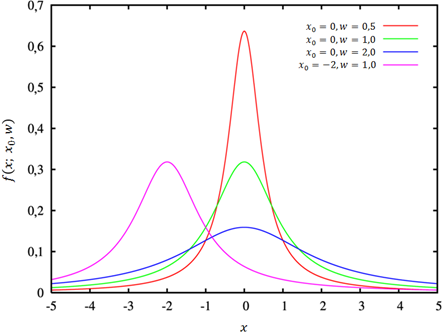
Figura 3. Función Lorentziana con valores específicos. Fuente de imagen base: Wikimedia. Edición: Lic. Daiver Juarez, @djredimi2.
Esta función es usada en física como solución a la ecuación diferencial de los osciladores de resonancia forzada. El valor de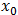 
describe, en este caso, al resonador oscilante. Si estamos en presencia de varios resonadores entonces la función Lorentziana se convierte en:
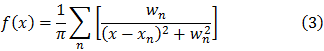
Sobre las relaciones de dispersión óptica.
Como ya veníamos hablando, las relaciones de dispersión están relacionadas con los valores de la función 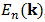, quienes describen a su vez a los valores de energía que no pueden ser ocupados por los electrones. Por ejemplo para la energía fundamental 
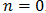, la brecha de energía fundamental pasa a ser 
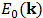. De esta manera podemos encontrar todos los valores de energía donde se observa la absorción óptica y describir la estructura de bandas de cualquier cristal.
Podemos obtener los valores de dispersión óptica de varias maneras. En este post emplearemos el uso de un modelo basado en la función Lorentziana para ajustar la curva de la función dieléctrica. Por lo tanto, empleando la ecuación del oscilador armónico Lorentziano, podremos realizar un ajuste aproximado la función dieléctrica por medio de:
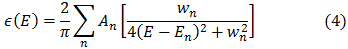
Donde 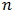es el índice particular del oscilador, 
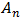es su amplitud, 
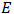es la energía de los fotones, 
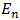es el punto central de la energía del oscilador y 
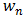es coeficiente de amortiguación del oscilador.
Ajuste sobre la función dieléctrica del cristal semiconductor CdTe.
En el primer post sobre "ELIPSOMETRÍA ESPECTROSCÓPICA (SE)" les había mostrado resultados experimentales de las propiedades ópticas sobre una muestra de Teluro de Cadmio (CdTe), cristal que actualmente es potencialmente aplicable al uso de celdas solares.
En este caso se usó una muestra masiva de CdTe de espesor específico. El ajuste experimental se realizó mediante el software matemático Origin 6.1, y la ecuación de lorentz:
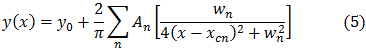
La figura 4, muestra el ajuste de la curva de la función dieléctrica imaginaria. Al final del texto se ANEXA un video relacionado con el ajuste de esta curva. Además, la varianza del ajuste entre los datos experimentales y los datos ajustados, Chi2, es aproximadamente igual cero. Y, la bondad del ajuste experimental es R2 = 0.998, del 1 para el modelo ideal.
Comparando las ecuaciones (4) y (5) tenemos que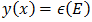 
, 
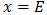y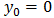 
.
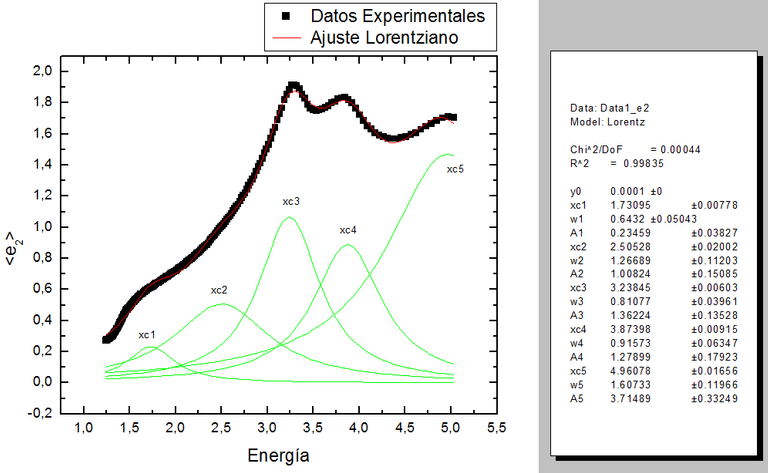
Figura 4. Ajuste experimental de la funcion de Lorentz a la curva de la función dielectrica imaginaria vs la energía sobre el cristal semiconductor CdTe. Fuente Propia: Lic. Daiver Juarez, @djredimi2.
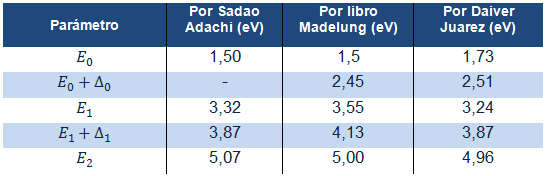
Los valores de las relaciones de dispersión, también conocidas como energías de banda, para el CdTe fueron por primera vez calculados por Sadao Adachi en 1993 mediante el uso de varios modelos matemáticos. El handbook de Madelung presenta los valores aceptados actualmente para las energías de la estructura de bandas del CdTe. La siguiente tabla establece una comparación entre los datos obtenidos por Sadao Adachi, los primeros 5 datos por Madelung y los obtenidos mediante este estudio por Lic. Daiver Juarez.
BIBLIOGRAFÍA CONSULTADA.
- John P. Mckelvey. (1976). "Física del estado sólido y de semiconductores". Mexico. Editorial Limusa. Capítulo 9.
- Sadao Adachi et al. (1993). "Optical properties of CdTe: Experiment and modeling". Joulnal Applied Physics 74, 3435.
- Otfried Madelung. (2004). "Semiconductors: Data Handbook". 3rd Edition. Springer-Verlag Berlin Heidelberg New York.
LECTURA RECOMENDADA.
MIT. Células solares de teluro de cadmio logran un nuevo récord de eficiencia.
@djredimi2 Te invita a formar parte de la sub-comunidad #stem-espanol, compartiendo temas de interés en Ciencias, Tecnologías, Ingenierías y Matemáticas en idioma Español. Cabe destacar que debes cumplir con las normas correspondientes, las cuales puedes ubicar en el perfil de @carloserp-2000, quien es miembro de la comunidad #steemstem.
Saludos @djredimi2. Excelente Trabajo y aporte para la comunidad.
Saludos profe. Gracias por su comentario
Excelente trabajo amigo @djredimi2 siempre nos enseñas de manera sencilla y practica la ciencia de la física.
Gracias estimado @ajpacheco1610. Si, es que la física puede ser estudiada de muchas formas, con diferentes herramientas, pero la dificultad de ella dependerá del autor que la estudie.
Excelente amigo @djredimi2 es muy importante poder impartir todos tus conocimientos de una manera sencilla y practica para que observadores como yo que nos dedicamos a otras áreas podamos entenderla y disfrutarla. Como te habia comentado ya esta disponible mi nuevo trabajo sobre una Necropsia de un Conejo espero te guste.
Hi @djredimi2!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thanks you @utopian-io