Qué tal mis queridos amigos de STEEM.
Hoy les traigo un nuevo post referente al estudio de los materiales semiconductores. En esta oportunidad, les estaré compartiendo sobre un Método experimental para medir la Resistividad Eléctrica de Muestras de geometría arbitraria que fue propuesto en 1958 por J. van der Pauw [1]. A lo largo de este post, se estará dando un análisis detallado de este método así como de su fundamento teórico.
Del día de mi Tesis @djredimi2
Debo destacar que hace aproximadamente 9 meses, compartí una porción de este método en versión inglés (ver aquí). También se incluyó este método en un post donde presenté algunos resultados de mi Tesis (ver aquí también)
En muchos casos, la resistividad eléctrica específica de un material conductor es medido por una muestra cortada en forma de barra. Generalmente, se disponen una serie de contactos que unen al material con los electrodos de prueba. En la figura 1, La corriente eléctrica entra por el contacto A y sale por el contacto B, y la diferencia de potencial es medida entre los contactos C, D, E y F. La resistividad específica deriva desde la caída de potencial sobre los contactos C y D, o E y F y desde las dimensiones de la muestra (Esto podría ser otro post).
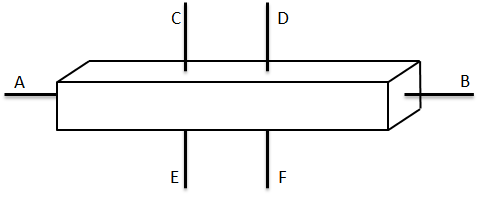
Figura 1. Medida de la resistividad eléctrica específica de un material cortado en forma de barra | por @djredimi2
Para las medidas de resistividad eléctrica de semiconductores generalmente suele ser usado una forma mas complicada. Una de ellas es la muestra en forma de puente (bridge-shaped) (figura 2). Las grandes áreas en los extremos tienen la tarea de proporcionar contactos óhmicos. Esta técnica tiene sus consideraciones por lo que es de vital importancia realizar un estudio más profundo.
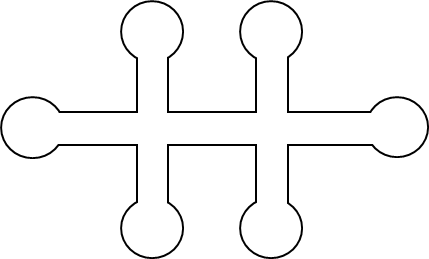
Figura 2. Muestra en forma de puente (bridge-shaped) | por @djredimi2
El autor, van de Pauw, no desacredita para nada este método experimental. Más bien, generaliza los detalles técnicos de este, ampliando su aplicabilidad. Debo destacar, que las mejoras que presenta este método varían entorno a los equipos de corte y el tamaño de la muestra. Es decir, al mejor aprovechamiento de las muestras de cualquier geometría y tamaño, pero homogéneas y con espesor específico.
Entrando en tema, consideraremos una muestra plana de un material conductor de geometría arbitraria con contactos sucesivos A, B, C y D fijos sobre lugares arbitrarios a lo largo de la circunferencia y con contactos pequeños (figura 3).
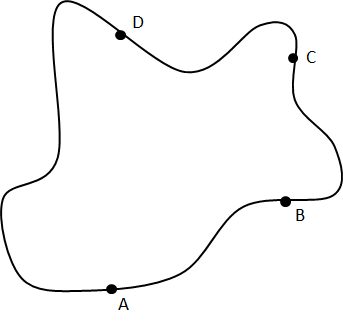
Figura 3. Contactos sobre una superficie plana de geometría arbitraria para determinar la resistencia eléctrica específica. | por @djredimi2
Definimos la resistencia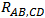 
como la diferencia de potencial 
sobre los contactos D y C por unidad de corriente a través de los contactos A y B. La corriente eléctrica entra a la muestra por el contacto A y sale a través de l contacto B. De manera similar definimos la resistencia 
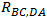. De esta manera, introducimos la siguiente relación.
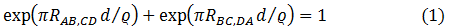
Donde,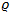 
es la resistividad eléctrica específica del material y 
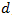es el espesor de la muestra.
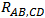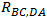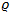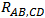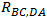Una aplicación practica de este teorema es para medir la resistividad eléctrica específica de una muestra plana de espesor específico. A lo largo de la circunferencia, y con el uso de contactos óhmicos, se miden las resistencias y (según figura 3). La ecuación (1) determina únicamente el valor de como una función de las resistencias y y . Esta ecuación puede ser reescrita como:
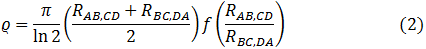
donde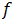 
es una función de la relación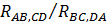 
y se le conoce como el factor geométrico. Este factor satisface la la ecuación
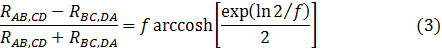
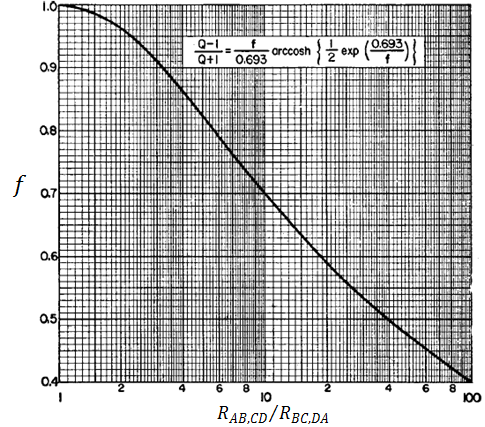
Figura 4. Función del factor geométrico en función de la resistencia, para determinar la resistividad específica de una muestra | por @djredimi2
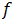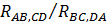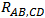En la figura 4, se muestra la gráfica de en función de . Si y 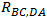son aproximadamente iguales, el factor geométrico puede ser aproximado a:
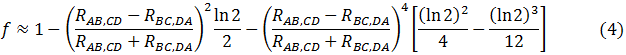
El análisis mostrado en este post fueron publicados en 1958, y se conoce como el "Método van der Pauw". Sin embargo, a pesar de la ambigüedad de esta publicación, es de vital importancia para el estudio de la resistividad eléctrica de materiales semiconductores.
En el laboratorio de Energías Alternativas de la Universidad del Zulia )Venezuela), se encontró un problema de una muestra que había sido sintetizada y que al obtener el lingote final, se cortó en forma de oblea de geometría irregular. Para realizar los estudios de las propiedades eléctricas, se procedió a tomar este método debido a la imposibilidad de obtener una barra de la muestra.
Esta muestra, en forma de oblea, pero de geometría arbitraria, resultó en la investigación de mi Trabajo Especial de Grado (Tesis). Se determinó la resistividad eléctrica del compuesto Ag2PbTe3 a través del uso del método van der Pauw.
En un siguiente post, espero compartir con ustedes el famoso método de barra, en materiales conductor y semiconductores.
Att. Licenciado en Física Daiver Juarez, @djredimi2.
[1] van der Pauw, J. (1958). “A method of measuring specific resistivity and Hall Effect of discs of arbitrary shape”. Volumen 13. Eindhoven, Netherlands. Philips Research Reports. P.1-9.
[2] ASTM F76-08 International. (2011). “Standard Test Methods for Measuring Resistivity and Hall Coefficient and Determining Hall Mobility in Single-Crystal Semiconductors”. Pennsylvania, EEUU. P.1-7.
[3] Juárez, Daiver. (2017). "Parámetros eléctricos en función de la temperatura del semiconductor Ag2PbTe3". Trabajo especial de grado presentado para optar al título de licenciado en Física. Venezuela, Maracaibo, Edo-Zulia. Universidad del Zulia.
Si estás interesado en unirte al grupo de Física, te invito cordialmente a chat oficial de #stem-espanol, registrándote en discordapp.com y accediendo a este enlace.
Conoce todo sobre el logo visitando este enlace.
Para saber más sobre STEM visita el canal principal @stem-espanol y el canal general @steemstem.
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Gracias Amigos.
Congratulations @djredimi2! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Saludos @djredimi2. Un trabajo excelente el que nos traes. Mis felicitaciones.
Gracias Profesor @lorenzor.
Interesante método de medición de la resistividad eléctrica. Saludos.
Que bueno que te haya sido interesante. Estimado @ydavgonzalez
Hola @djredimi2 felicitaciones por tu presentación de tesis. No se si es primera vez que se utiliza esa manera de medir resistividad en semiconductores? Que ventaja tiene esa forma de medir con la forma tradicional de medir la resistividad en los semiconductores?
Saludos @germanmontero. No es la primera vez. Es algo antiguo este método. Sin embargo la aplicabilidad ha sido ampliada y actualizada. El artículo ASTM F76-08 aplica una actualización para este método.
Con respecto a las ventajas, siempre varían de acuerdo a la necesidad del laboratorio. Por ejemplo, hay materiales que al ser sintetizados no son duros, por lo que es muy complicado cortarlos en la forma de barra. Tener acceso a un método que sólo exige un espesor homogéneo es muy bueno. Entre otras ventajas.