INTRODUCCIÓN
La ocurrencia de los sismos y los efectos que estos tienen en las estructuras, dejan enseñanzas sobre el desempeño o comportamiento de estas, para la disipación de la energía introducida por el sismo, más allá del rango de comportamiento elástico (evidencia de daño). En la imagen N°01 podemos apreciar, el colapso de dos edificaciones escolares, ante el sismo de Cariaco de 1997, donde uno de los principales aspectos que hizo vulnerable a tales estructuras ante las solicitaciones provocadas por la acción del sismo, fue la presencia de columnas cortas. En las escuelas que aparecen debajo de las colapsadas, se resalta con un óvalo rojo, esta vulnerabilidad estructural.
Imagen N°01: estudio del efecto “columna corta” con diagramas de interacción “flexión-carga axial-corte”
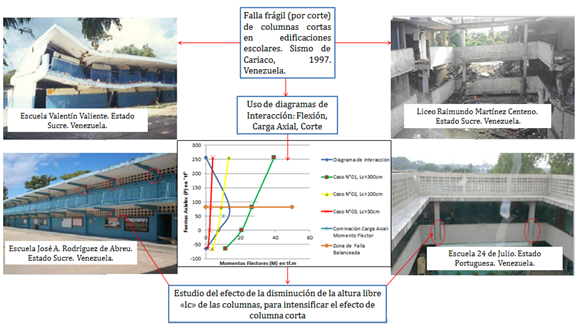
Fuente: López (2011), adaptado por Santana (2018)
En este artículo aprenderemos a cuantificar por medio del uso de diagramas de interacción “flexión-carga axial-corte” representados por los gráficos de colores “verde, amarillo y rojo” (ver imagen N°01) los efectos que puede tener la disminución de la altura libre de deformación de las columnas, debido a la presencia de paredes, muros y otros elementos tanto estructurales como no estructurales. Se recomienda al lector, la revisión de la referencia N°05, donde se profundiza en la construcción de diagramas de interacción “flexión-carga axial” representado por el gráfico de color “azul”, de una columna de sección cuadrada de concreto armado; constituyendo la base para la incorporación de los diagramas de interacción “flexión-carga axial-corte”, los cuales marcan una frontera entre la falla por flexión (comportamiento dúctil) y la falla por corte (comportamiento frágil); especialmente cuando estos diagramas, reducen la región efectiva de interacción de valores de carga axial “P” y momento flector “M”.
DELIMITACIÓN DEL CASO EN ESTUDIO
La columna en estudio está construida de concreto armado, y en la tabla N°01 se hace un resumen de las propiedades de los materiales constituyentes, es decir: concreto y acero. Se recomienda al lector la revisión de la referencia N°07, para que profundice en estos aspectos.
Tabla N°01: resumen de las propiedades de los materiales a trabajar

Fuente: Santana (2018)
La geometría de la sección y el acero de refuerzo tanto longitudinal como transversal de la misma, se pueden apreciar en la imagen N°02:
Imagen N°02: datos generales de la sección transversal y elemento estructural
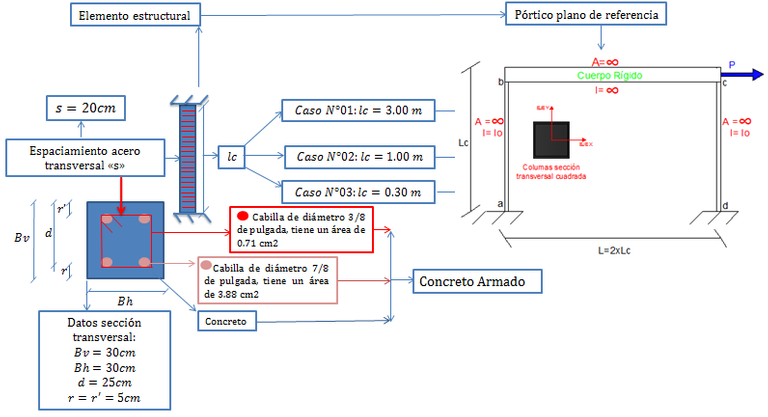
Fuente: Santana (2018)
De acuerdo a lo ilustrado en la imagen N°02, se está en presencia de una sección transversal cuadrada, cuyo diagrama de interacción “flexión-carga axial” es conocido (ver referencia N°05); el cual será tomado como base, para la inclusión de los efectos de esfuerzos por corte, donde interviene el espaciamiento del acero de refuerzo transversal (s), considerando en este estudio una separación “s=20cm”, y una altura de columna “lc”, ajustada a tres casos de interés, disminuyendo en cada uno de ellos los valores de “lc”, para así emular la condición de columna corta. Adicionalmente conviene estudiar la estática involucrada en el pórtico de la imagen N°02, donde se deduce la ecuación fundamental para la construcción del diagrama de interacción “flexión-carga axial-corte”.
Imagen N°03: pórtico plano de referencia
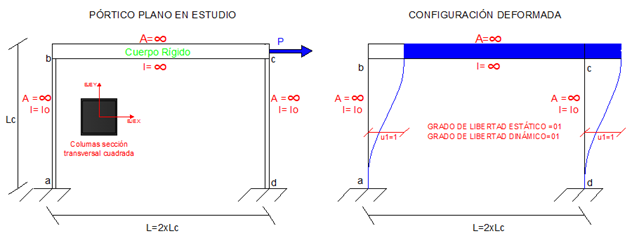
Fuente: Santana (2018)
De acuerdo a la imagen N°03, se tiene un pórtico de un grado de libertad estático y un grado de libertad dinámico; en la referencia N°06, el lector podrá profundizar en el análisis matricial involucrado en estos problemas. Por lo que ahora concierne, tomemos como referencia, un elemento vertical “columna” del pórtico en cuestión:
Imagen N°04: columna idealizada con junta “b” imposibilitada de rotar y de experimentar desplazamiento vertical
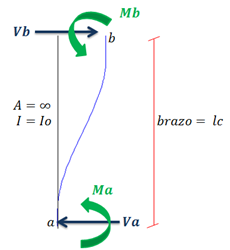
Fuente: Santana (2018)
El hecho de que la estructura posea columnas con propiedades de área “A= ∞”, es decir, que no pueden experimentar acortamiento ni alargamiento; y que el elemento horizontal sea un cuerpo rígido; produce la condición de que la junta “b” no experimente rotación ni desplazamiento vertical, obteniéndose por lo tanto un grado de libertad estático. Lo cual aunado al hecho de que la junta “a” posea un empotramiento que imposibilita la rotación, así como los desplazamientos tanto vertical como horizontal de la misma; permite establecer en pro de garantizar el equilibrio estático de la columna, lo siguiente:
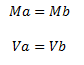
Por lo que al hacer momento en “a”, se obtiene:
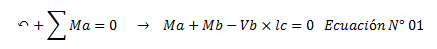
Partiendo de la suposición hecha de cortantes iguales y momentos iguales, la ecuación N°01 se puede rescribir así:
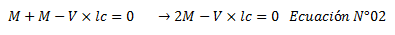
Despajamos “M” de la ecuación N°02:
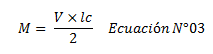
Esta ecuación es la que utilizaremos para la construcción del diagrama de interacción “flexión-carga axial-corte”, que va a representar, una disminución en el caso que lo intercepte, de la región de interacción de valores de flexión y carga axial de la sección transversal de la columna (gráfico de color “azul”), marcando la frontera entre un comportamiento dúctil y un comportamiento frágil; lo cual se ilustra didácticamente en la imagen N°05.
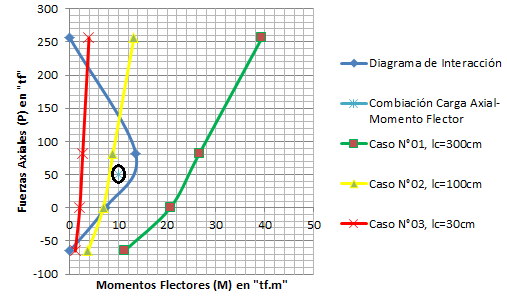
Imagen N°05: reducción de la región efectiva de interacción “flexión-carga axial”, gráfico de color “azul”
Fuente: Santana (2018)
De acuerdo a la imagen N°05, se aprecia que para los distintos diagramas “flexión-carga axial-corte” representados por los gráficos de colores “verde, amarillo y rojo”; el más crítico es el gráfico de color “rojo”; porque es el que disminuye en mayor medida la región efectiva de interacción “flexión-carga axial”, representada por el gráfico de color “azul”. Esto se demuestra, al tomar como referencia el punto resaltado en color negro, representativo de una combinación de carga axial “P” y momento flector “M”, que para el caso del diagrama resaltado en color “verde”, no se origina falla frágil, mientras que para los casos de los diagramas de colores “amarillo” y “rojo”, esta si se produce; y en estructuras esto es un manifiesto de las consecuencias que pueden tener la presencia de columnas cortas. Profundicemos un poco más en la filosofía de los diagramas de interacción “flexión-carga axial-corte”.
FILOSOFÍA DE LOS DIAGRAMAS DE INTERACCIÓN “FLEXIÓN, CARGA AXIAL, CORTE”
La elaboración de los diagramas de interacción “flexión-carga axial-corte”, para el estudio del efecto de columna corta, se fundamenta en lo planteado en la imagen N°06.
Imagen N°06: evaluación de métodos para predecir el comportamiento sísmico de edificios de concreto armado
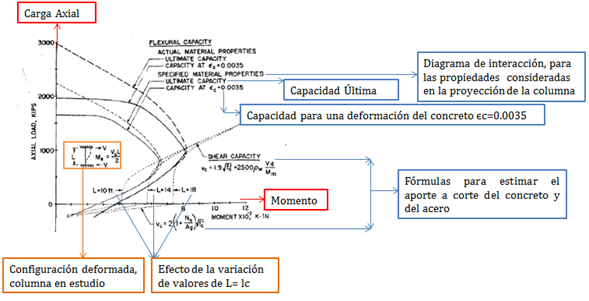
Fuente: Mahin y Bertero (1975), adaptada por Santana (2018)
En el gráfico de la imagen N°06, podemos apreciar un diagrama de interacción “flexión-carga axial” de una sección transversal de concreto armado, que se encuentra interceptado por unas líneas segmentadas, que vienen siendo los diagramas de interacción “flexión-carga axial-corte” para diversos casos de altura de columnas. Y que representan la frontera entre un comportamiento dúctil “falla por flexión” y un comportamiento frágil “falla por corte”; dado que en los casos en los que se restringe el diagrama original de la sección (cuando hay presencia de columnas cortas), las combinaciones de carga axial “P” y momento “M” que queden a la derecha de esta frontera, son un indicativo de falla frágil, afianzando de este modo, lo ilustrado en la imagen N°05.
Si bien estos diagramas de interacción “flexión-carga axial-corte” se construyen con valores de carga axial “P” y momento “M”; este último valor, es función del máximo corte que el elemento estructural pueda resistir (ver ecuación N°03), por lo que valores de momento mayores a los que demarca este diagrama en cuestión, van a representar mecanismos de falla frágil (falla por corte), y que se acrecientan, en la medida que la columna se hace más corta, cuya presencia lamentablemente es una realidad en muchas edificaciones; como es el caso de las edificaciones escolares mostradas en la imagen N°01.
Dado que un dato importante, en la construcción de los diagramas de interacción “flexión-carga axial-corte” lo constituye la estimación de la resistencia a corte del elemento estructural, conviene señalar las disposiciones normativas al respecto. Para el caso de esfuerzos de flexión y carga axial a compresión, el apartado 11.3 de FONDONORMA 1753:2006, señala:
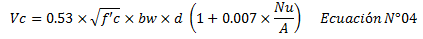
Dónde:
Vc, resistencia a corte del concreto
f’c, resistencia a compresión del concreto
bw, base de la sección transversal, para el caso en estudio es “Bv”
d, altura útil de la sección transversal
Nu, carga axial
A, área de la sección transversal, para el caso en estudio viene dada por:
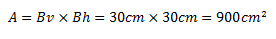
Cuando se está en presencia de esfuerzo de flexión y carga axial a tracción, se desprecia el aporte de resistencia a corte del concreto, por lo que:
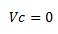
En lo que respecta al aporte a la resistencia a corte del acero “Vs”, en el apartado 11.4.3 de FONDONORMA 1753:2006, se establece la siguiente ecuación:
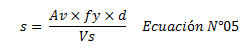
Dado que “s” corresponde al espaciamiento del acero transversal” y el mismo es fijado en este estudio de forma arbitraria (ver imagen N°02), debido a que el alcance de este artículo no es estudiar la influencia del espaciamiento del acero transversal, sino la de estudiar la influencia de la disminución de la altura de la columna “lc”. En un próximo post profundizaré, en lo referente al espaciamiento “s” del acero transversal en las labores de detallado de elementos de concreto armado. Continuando con el planteamiento de ecuaciones, despejemos el término “Vs” de la ecuación N°05:
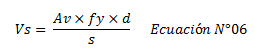
Dónde:
fy, es el límite de cedencia del acero
Av, área de refuerzo transversal
En relación al área del acero transversal, conviene explicar la forma de cuantificarlo en una sección transversal de una columna de concreto armado.
Imagen N°07: cuantificación del área de acero transversal “Av” en una sección transversal
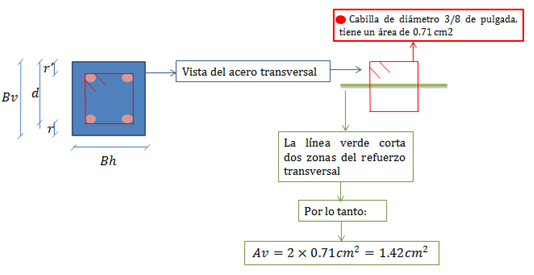
Fuente: Santana (2018)
Vale destacar que el aporte a la resistencia al corte del acero, estará presente, indistintamente que la carga axial se encuentre a tracción o compresión. Una vez aclarados los principales aspectos conceptuales en los que se fundamentan los diagramas de interacción “flexión-carga axial-corte”, procedamos a la obtención de los mismos, tomando como referencia los casos señalados en la imagen N°02.
APLICACIONES PRÁCTICAS
DIAGRAMA DE INTERACCIÓN “FLEXIÓN-CARGA AXIAL”
El diagrama de interacción “flexión-carga axial” de la sección transversal en estudio, se conoce y viene dado por los puntos presentados en la tabla N°02.
Tabla N°02: datos diagrama de interacción, columna de concreto armado de sección cuadrada

Fuente: Santana (2018)
Al graficar estos puntos se obtiene el diagrama de la imagen N°08:
Imagen N°08: diagrama de interacción “flexión-carga axial”
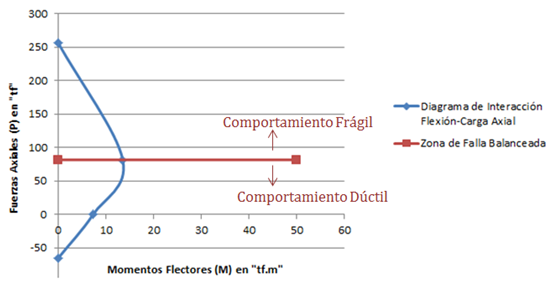
Fuente: Santana (2018)
Se recomienda al lector, la revisión de la referencia N°05, para que profundice en el proceso de construcción del diagrama de interacción “flexión-carga axial”.
ESTIMACIÓN DE LA RESISTENCIA AL CORTE
El aporte a la resistencia al corte del acero, se obtiene con la ecuación N°06, dependiendo por lo tanto de valores que permanecerán constantes a lo largo de los cálculos como lo son el espaciamiento “s”, el límite de cedencia del acero “fy”, la altura útil de la sección “d” y el área de acero transversal “Av”, cuyo cálculo se ilustra en la imagen N°07. Por lo tanto:
s=20 cm
fy=4200 kgf/cm2
d=25 cm
Av=1.42 cm2
Y sustituyendo en la ecuación N°06, los valores de longitud en “cm”, de área en “cm2” y de esfuerzo en “kgf/cm2”, se tiene lo siguiente:
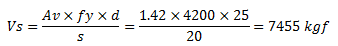
Por su parte, el aporte a la resistencia al corte del concreto si variará dependiendo los niveles de carga axial considerados, por lo que:
a.- Carga Axial P=Nu=256.43 tf=256430 kgf, asociada a la carga que produce la falla por compresión pura de la sección. Al sustituir en la ecuación N°04, los datos conocidos:
f’c=250 kgf/cm2
Bh=30cm
d=25cm
A=900cm2
Se obtiene lo siguiente:
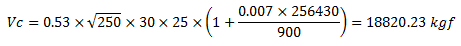
Por lo que el aporte total para para la resistencia al corte “Vt”, viene dado por:
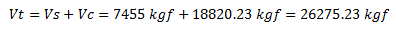
b.- Carga Axial P=Nu=81.28 tf=81280 kgf, asociada a la carga que produce la falla balanceada en la sección. Al sustituir en la ecuación N°04, los datos conocidos:
f’c=250 kgf/cm2
Bh=30cm
d=25cm
A=900cm2
Se tiene lo siguiente:
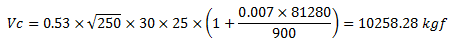
Por lo que el aporte total para para la resistencia al corte “Vt”, viene dado por:
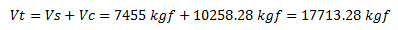
c.- Carga Axial P=Nu=0.00 tf=0.00 kgf, asociada a la falla por flexión pura de la sección (comportamiento similar al de una viga). Al sustituir en la ecuación N°04, los datos conocidos:
f’c=250 kgf/cm2
Bh=30cm
d=25cm
A=900cm2
Se tiene lo siguiente:
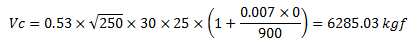
Por lo que el aporte total para para la resistencia al corte “Vt”, viene dado por:
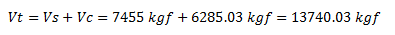
d.- Carga Axial que produce la falla a tracción pura P=65.18 tf = 65180 tf. En este caso, se desprecia el aporte a la resistencia al corte del concreto, por lo que el aporte total para para la resistencia al corte “Vt”, viene dado por:
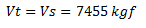
Una vez obtenidos los valores máximos de resistencia a corte de la sección de columna de concreto armado; se extrapolan al elemento estructural, con el uso de la ecuación N°03, donde los valores de momento “M” que se obtienen, al graficarse con respecto a la carga axial, constituyen los diagramas de interacción “flexión-carga axial-corte” y representan a su vez una frontera, entre el comportamiento dúctil (falla por flexión) y frágil (falla por corte) de la columna que se analiza; demostrándose en los cálculos que siguen, que mientras más corta es la columna, en esa misma proporción lo será su tendencia a fallar de forma frágil; por lo que se plantean tres casos de estudio:
CASO DE ESTUDIO N°01: lc=3m=300cm
Aplicando la ecuación N°03, para los diversos valores de resistencia al corte, se tiene lo siguiente:

Procedemos a construir la tabla de valores, para el diagrama de interacción “flexión-carga axial-corte”:
Tabla N°03: valores diagrama de interacción “flexión-carga axial-corte” para lc=3.00m=300cm

Fuente: Santana (2018)
Al graficar sobre el diagrama de interacción de la imagen N°08, los datos presentados en la tabla N°03, se obtiene lo siguiente:
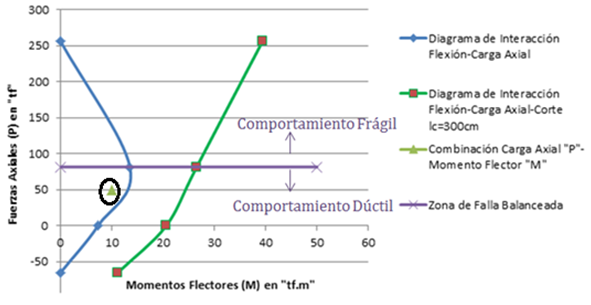
Imagen N°09: diagrama de interacción “flexión-carga axial-corte”, caso de estudio N°01
Fuente: Santana (2018)
El diagrama de interacción “flexión-carga axial-corte” representativo del elemento estructural (gráfico de color “verde”), no intercepta el diagrama de interacción de la sección transversal (gráfico de color “azul”); lo que significa que la columna, desarrollará su máxima resistencia a flexión, para lo niveles de carga axial por debajo del punto balanceado, garantizando de esta manera un comportamiento dúctil; es decir, la frontera que marca el diagrama de color “verde”, no restringe la región de comportamiento dúctil del diagrama en color “azul”.
Tomando como referencia una posible combinación de valores de carga axial “P=50 tf”, y momento flector “M=10 tf.m” (ver punto resaltado en óvalo negro de la imagen N°09), podemos concluir que no está comprometido el comportamiento dúctil de la sección, por el simple hecho de que la carga “P” está por debajo del punto balanceado (ver referencia N°05).
CASO DE ESTUDIO N°02: lc=1.00 m=100cm
Aplicando la ecuación N°03, para los diversos valores de resistencia al corte, se tiene lo siguiente:

Procedemos a construir la tabla de valores, para el diagrama de interacción “flexión-carga axial-corte”:
Tabla N°04: valores diagrama de interacción “flexión-carga axial-corte” para lc=1.00m=100.00cm

Fuente: Santana (2018)
Al graficar, sobre el diagrama de interacción de la imagen N°08, los datos presentados en la tabla N°04, se obtiene lo siguiente:
Imagen N°10: diagrama de interacción “flexión-carga axial-corte”, caso de estudio N°02
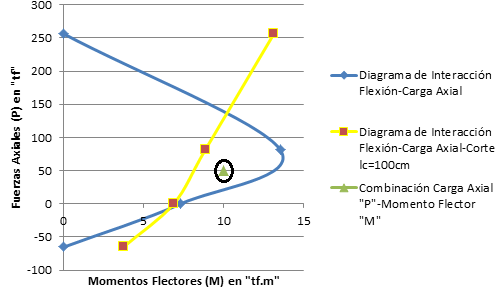
Fuente: Santana (2018)
Cuando la altura de la columna disminuye a un metro, lo cual puede ocurrir por deficiencias conceptuales desde el punto de vista sismoresistente al construir la edificación, originando la presencia de una columna corta (ver imagen N°01), apreciamos que el diagrama de interacción “flexión-carga axial-corte” representado por el gráfico de color “amarillo”, interrumpe la región perteneciente al diagrama de interacción “flexión-carga axial” representado por el gráfico de color “azul”, lo que origina, que la combinación de carga axial “P=50tf” y momento flector “M=10tf.m” (ver punto resaltado con el óvalo negro), quede a la derecha de la frontera que marca el comportamiento dúctil (falla por flexión) y el comportamiento frágil (falla por corte); es decir, para esta combinación de esfuerzos, la columna fallaría de forma frágil, comportamiento típico de una columna corta, muy distinto a lo que ocurre, en el diagrama de la imagen N°09, donde la región que encierra el diagrama de color “azul” no está interrumpida por el diagrama de interacción “flexión-carga axial-corte”.
CASO DE ESTUDIO N°03: lc=0.30 m=30cm
Aplicando la ecuación N°03, para los diversos valores de resistencia a los cortes obtenidos, permite:

Procedemos a construir la tabla de valores, para el diagrama de interacción “flexión-carga axial-corte”:
Tabla N°05: valores diagrama de interacción “flexión-carga axial-corte” para lc=0.30m=30.00cm

Fuente: Santana (2018)
Al graficar sobre el diagrama de interacción de la imagen N°08, los datos presentados en la tabla N°05, se obtiene lo siguiente:
Imagen N°11: diagrama de interacción “flexión-carga axial-corte”
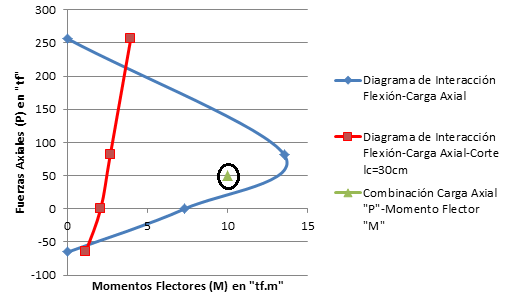
Fuente: Santana (2018)
Este caso, sin lugar a dudas representa un caso extremo, en el que la altura libre de deformación de la columna ha disminuido a “lc=30cm”, lo que produce que el diagrama “flexión-carga axial-corte” representado por el gráfico de color “rojo”, restringa mucho más de un 50% la región que encierra el diagrama de interacción “flexión-carga axial” de la sección, representado por el gráfico color “azul”. Este es un caso, mucho más desfavorable que el caso de estudio N°02, y por supuesto el punto resaltado con el óvalo negro, representativo de una combinación de carga axial “P” y momento flector “M”, produce una falla frágil.
Este tipo de columnas tan cortas, es típico apreciarlas en edificaciones escolares construidas con sistemas aporticados “vigas y columnas”, donde existen cerramientos con paredes de ladrillos o de bloque, como se aprecia en la siguiente imagen:
Imagen N°12: colapso de columna corta en edificaciones escolares, por la acción de terremotos
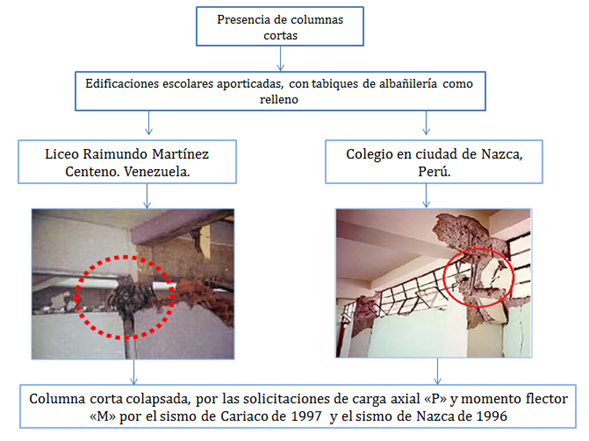
Fuente: López (2011), Ref. N°03 (2012), adaptada por Santana (2018)
Se observa como la ocurrencia de sismos severos, pone a prueba esta vulnerabilidad en la estructura, y el desempeño de la misma, se caracteriza por ser de tipo frágil, lo cual puede resultar en pérdidas de muchas vidas humanas, por el posible colapso de la estructura.
CONCLUSIONES
Las conclusiones de este trabajo, se centran en sintetizar aquellos aspectos claves de mayor impacto en la práctica de la ingeniería sismoresistente, por lo que nos valemos del diagrama de la imagen N°13, el cual resume todos los casos estudiados:
Imagen N°13: diagramas de interacción “flexión-carga axial-corte”
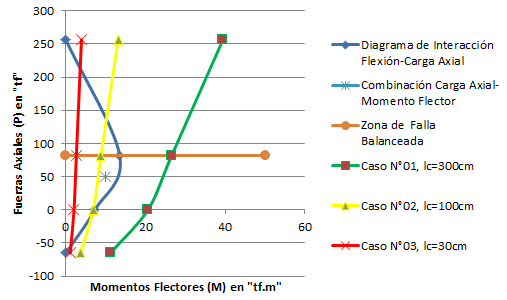
Fuente: Santana (2018)
Estas conclusiones son:
1.- Si la columna de concreto armado, no se le es interrumpida su altura libre de deformación una vez construida a causa de la presencia de elementos estructurales o no estructurales (por ejemplo: muros, paredes y otros), esta se comportará conforme a las hipótesis establecidas en el diagrama de interacción flexión-carga axial (gráfico de color “azul”); en lo referente a que el comportamiento dúctil o frágil, está delimitado por la frontera que constituye la zona de falla balanceada.
2.- Al ocurrir una disminución abrupta de la altura libre de deformación de la columna “lc”, los diagramas de interacción “flexión-carga axial-corte”, reducen la región efectiva de interacción para combinación de valores de carga axial “P” y momento flector “M”, como ocurre con los diagramas resaltado por los colores “rojo” y “amarillo”.
3.- La disminución de la región efectiva de interacción de valores de carga axial “P” y momento flector “M”, produce condiciones de falla frágil, para combinación de valores que queden a la derecha, de los diagramas de interacción “flexión-carga axial-corte” representados por los gráficos de color “rojo” y “amarillo” de la imagen N°13; lo cual pone en evidencia la vulnerabilidad que representan las columnas cortas en un sistema estructural, lo que cobra, más importancia aún, cuando ese sistema estructural es responsable de resistir acciones sísmicas.
4.- En sistemas aporticados, constituidos por vigas y columnas, estas son las garantes de la estabilidad de la estructura; incluso, cuando se busca que la estructura disipe la energía introducida por un sismo, más allá del comportamiento elástico, a través de la presencia de daño, se busca que este daño ocurra en las vigas, a través de articulaciones plásticas, es por eso, que en diseños sismoresitentes la filosofía de columna fuerte-viga débil, es muy utilizada.
5.- Los mecanismos de falla dúctil, están representados por fallas a flexión, en los que se produce gradualmente la cedencia y agotamiento de los materiales constituyentes del concreto armado; por su parte, los mecanismos de falla frágil, representan una pérdida abrupta de resistencia, que aleja la estructura de un comportamiento dúctil.
REFERENCIAS BIBLIOGRÁFICAS Y FUENTES CONSULTADAS
1.- LÓPEZ OSCAR. REDUCCIÓN DEL RIESGO SÍSMICO EN EDIFICACIONES ESCOLARES DE VENEZUELA. PROYECTO FONACIT N°2005000188. INFORME TÉCNICO 15 DE JULIO DE 2011.
2.- MAHIN S.A Y BERTERO V.V. AN EVALUATION OF SOME METHODS FOR PREDICTING SEISMIC BEHAVIOR OF RC BUILDINGS. EARTHQUEAKE ENGEENERING CENTER, BERKELEY. CALIFORNIA. 1975.
3.-COLUMNAS CORTAS EN EL DISEÑO ESTRUCTURAL. DISPONIBLE EN: http://ingenieriasismicaylaconstruccioncivil.blogspot.com/2012/11/columnas-cortas-en-el-diseno-estructural.html, CONSULTADA POR EL AUTOR EL 12 DE MARZO DEL 2018.
4.-NORMA VENEZOLANA “PROYECTO Y CONSTRUCCIÓN DE OBRAS EN CONCRETO ESTRUCTURAL". FONDONORMA 1753:2006. 1ERA REVISIÓN.
5.- SANTANA ELÍAS, 2018. APRENDIENDO A CONSTRUIR EL DIAGRAMA DE INTERACCIÓN DE UNA COLUMNA DE CONCRETO ARMADO. APLICACIONES EN LA INGENIERÍA SISMORESISTENTE. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/aprendiendo-a-construir-el-diagrama-de-interaccion-de-una-columna-de-concreto-armado-aplicaciones-en-la-ingenieria
6.- SANTANA ELÍAS, 2018. ESTUDIO DE LAS APLICACIONES DEL ANÁLISIS MATRICIAL EN LA OBTENCIÓN DE LA MATRIZ DE RIGIDEZ DE UN PÓRTICO PLANO. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-de-las-aplicaciones-del-analisis-matricial-en-la-obtencion-de-la-matriz-de-rigidez-de-un-portico-plano
7.- SANTANA ELÍAS, 2018. ESTUDIO DEL COMPORTAMIENTO DE VIGAS DE CONCRETO ARMADO DE SECCIÓN RECTANGULAR, TOMANDO COMO REFERENCIA LOS ESTADOS DE AGRIETAMIENTO, CEDENCIA Y AGOTAMIENTO DE LA SECCIÓN. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-del-comportamiento-de-vigas-de-concreto-armado-de-seccion-rectangular-tomando-como-referencia-los-estados-de