LEY DE ENFRIAMIENTO DE NEWTON UNA FORMA ALTERNA DE MEDIRLA
Newton observó que al calentar al rojo una barra de hierro y tras retirarla del fuego, la barra se enfriaba más rápidamente cuando estaba muy caliente y más lentamente cuando su temperatura se acercaba a la temperatura ambiente. Sus observaciones dieron lugar a lo que hoy conocemos con el nombre de ley de enfriamiento de Newton.
Las aplicaciones más notables de esta ley se visualizan en:
- Enfriamientos de cuerpos en el entorno
- En la ciencia forense. La criminalística se encarga de calcular el tiempo de enfriamiento de un cadáver. En esta medida se puede determinar con buena aproximación el tiempo de fallecimiento del cuerpo
- Modelos climáticos. En la evolución de la temperatura de la atmósfera
- En el control de temperatura de un procesador (computador)
Introducción
En los cursos de física universitaria, los experimentos de laboratorio tradicionales por lo general tienen como objetivo comprobar un principio o un concepto que los alumnos ya han aprendido por parte del instructor y la aplicación de estos experimentos es utilizar y sintetizar conceptos de la física desarrollados y probados anteriormente.
El propósito de este post tiene como objetivo presentar una nueva técnica experimental automatizada para comprobar la Ley de Enfriamiento de Newton y de estas pruebas experimentales, es posible manejar los datos, observar el comportamiento instantáneo de la temperatura en función del tiempo, inclusive realizar un análisis de los resultados bien sea en la misma calculadora o extraer los datos para manejarlo en un software de gráficas en el computador.
Una práctica de laboratorio de física que se realiza comúnmente es la de la Ley de Enfriamiento de Newton, que consiste en calentar una muestra metálica hasta a una cierta temperatura y posteriormente dejar que se enfrié hasta alcanzar la temperatura del medio circundante. Por otra parte, muchas de estas prácticas experimentales se realizan de forma cualitativa, observándose solo el fenómeno; y en otros casos se cuantifica tomando los datos de manera manual.
Fundamentos Teóricos
La Ley de enfriamiento de Newton establece que la rapidez de la variación de la temperatura es proporcional a la diferencia de la temperatura del cuerpo y su alrededor. Por consiguiente la ecuación diferencial que rige esta ley está dada por:
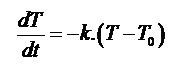 (1)
(1) donde: dT/dt representa la rapidez del enfriamiento, T es la temperatura instantánea del cuerpo, k una constante que define el ritmo de enfriamiento y To es la temperatura ambiente, que es la temperatura que alcanza el cuerpo luego de suficiente tiempo.
Si el cuerpo se enfría a partir de una temperatura inicial Tm hasta T, la solución a la ecuación (1) es:
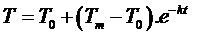 (2)
(2) esta ecuación representa la evolución de la temperatura con respecto al tiempo.
Montaje Experimental
Mediante la experimentación se observará, la variación de la temperatura en función del tiempo de una varilla metálica que se enfría hasta alcanzar la temperatura del medio circundante (laboratorio). Se analizan los resultados usando métodos gráficos, en el marco de la ley de enfriamiento de Newton.
Para el montaje experimental se emplea el equipo completo de Expansión Térmica Lineal de Sólidos Metálicos, el cual es empleado en las prácticas tradicionales de Dilatación Lineal De Sólidos Metálicos y a su vez en la demostración de la ley de enfriamiento de Newton.
Lo novedoso de esta prueba consiste en emplear unos instrumentos tecnológicos que están compuestos por una calculadora Casio Class Pad 300 Plus (http://edu.casio.com/, http://classpad.net/, http://www.casio-intl.com/) y un Data Analyzer EA-200 CASIO, el cual está diseñado para medir y registrar cantidades físicas tales como temperatura, sonido, voltaje, entre otras cantidades físicas. El sensor de temperatura y el Data Analyzer EA-200 son provisto por la CASIO.
Para este caso se coloca el sensor de temperatura en el tubo de expansión lineal conectado con un Data Analyzer y esté conectado a la calculadora gráfica. Para optimizar el experimento se uso programa Econ -200, que esta dentro de la calculadora y se procedió a realizar la medida . En la Figura 1 se muestra una foto de la configuración experimental para comprobar dicha ley.

Figura 1. Fotografía del Montaje experimental. Foto propia del autor. @germanmontero
El procedimiento experimental es el siguiente:
a) Se toma una de las varillas de metálicas (aluminio) se mide su longitud L (±1 mm) y la temperatura ambiente To (±1ºC), medida con un termómetro de Hg.
b) Se ensambla el equipo de expansión lineal como se indica en la Figura 1
c) Se enciende el sistema de calentamiento para generar el vapor de agua; hasta que la temperatura se eleve al máximo (aproximadamente 100 ºC).
d) Se toman la temperatura máxima. Se desconecta el sistema de vapor, en este momento se ajusta la medida de la temperatura en el programa Econ 200 instalado en la calculadora con la interface, y se comienza a registrar el descenso de la temperatura en función del tiempo.
e) Se repite todo el proceso anterior para la varilla metálica de cobre
Resultados y Análisis
Usando la técnica experimental explicada anteriormente, se observó el descenso exponencial de la temperatura en función del tiempo representado en la Figura 2, con su respectivo ajuste exponencial realizado en la misma calculadora gráfica.

Figura 2. Gráfica del comportamiento del enfriamiento de Newton con su respectivo ajuste visualizada en la calculadora. Imagen propia del autor. @germanmontero
Una ves extraídos los datos de la calculadora se utiliza el programa Origin versión 8.5 (www.originlab.com) para realizar el ajuste de las curvas obtenidas de estos datos. Las curvas resultantes, como se puede observar en las Figuras 3 y 4 son exponenciales.
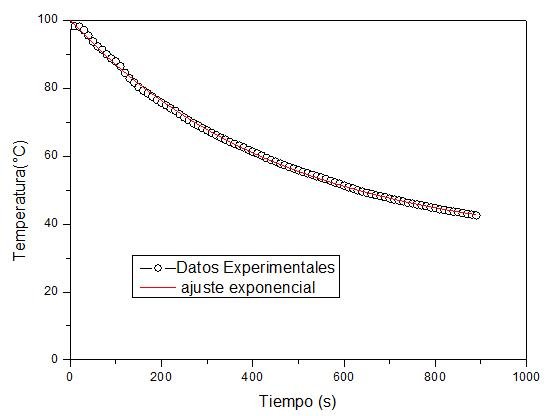
Figura 3. Gráfica resultante del ajuste exponencial del comportamiento de enfriamiento de la varilla de aluminio (Al). Imagen propiedad de @germanmontero
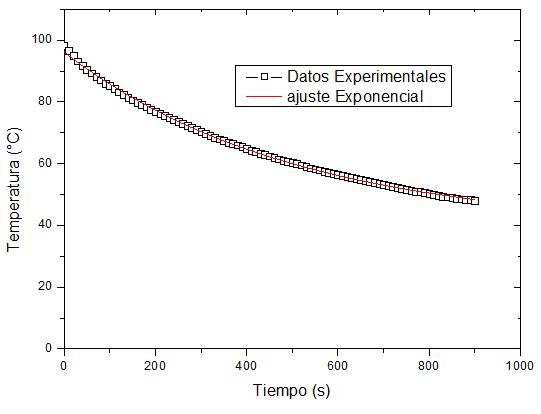
Figura 4. Gráfica resultante del ajuste exponencial del comportamiento de enfriamiento de la varilla de cobre (Cu) Imagen propiedad de @germanmontero
El modelo exponencial utilizado por el programa es:
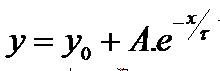 (3)
(3)comparando esta ecuación (3) con la ecuación (2), se tiene que:
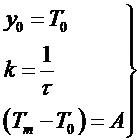 (4)
(4)De esto se obtiene que los respectivos valores para las varillas metálicas utilizadas se pueden observaren la Tabla 1, con sus respectivas desviaciones estándar.
Tabla propiedad de @germanmontero
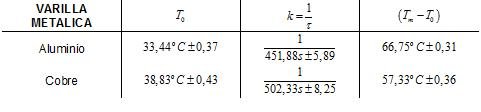
Escribiéndolo en forma de ecuación y calculando K para cada varilla se obtiene que:
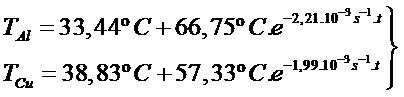 (5)
(5) Esta ecuación (5) representa el comportamiento de la temperatura (T ) en función del Tiempo (t ) del sistema en estudio.
Igualmente, de la ecuación (4) y de la Tabla 1 tenemos que:
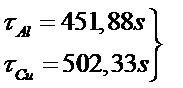 (6)
(6) donde
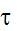 es la "constante de tiempo" y una medida del tiempo de respuesta del sistema. Que es semejante a un circuito eléctrico en el que se carga o descarga un condensador a través de una resistencia.
es la "constante de tiempo" y una medida del tiempo de respuesta del sistema. Que es semejante a un circuito eléctrico en el que se carga o descarga un condensador a través de una resistencia.
Conclusiones
El objetivo se logró de manera excelente, logrando en este experimento, una manera no convencional de medir la ley de enfriamiento de Newton, utilizando en primer lugar equipos tecnológicos tales como calculadora Casio 300, interfaces y sensor de temperatura Pasco, que se utilizan para captar datos de manera rápida, eficiente e instantánea.
Los resultados obtenidos empleando por esta técnica novedosa reproducen claramente el comportamiento exponencial de la temperatura (T) en función del tiempo (t) visualizando la gráfica alcanzada en la calculadora, lo cual se puede analizar matemática y físicamente dando resultados aceptables con la teoría.
Utilizando este equipo se puede manipular los datos dentro de la calculadora y a su vez pueden ser extraídos de ésta, donde se procesan en un programa graficador y se realiza un mejor análisis de estos resultados.
Referencias
Carrasco G. (2002). Enfriamiento de un cuerpo. Estudio de la ley de enfriamiento de Newton. E.E.T N°3 Florencio Valera, Buenos Aires. Red Creativa de Ciencia – Curso II –. Dirección electrónica: http://www.cienciaredcreativa.org/informes/enfriam_carrasco.pdf
Etkina E., Van Heuvelen A., Brookes D.T., Mills D.. (2002). Role of Experiments in Physics Instruction — A Process Approach, The Physics Teacher pp 351-355, Vol. 40, September. Dirección electrónica: tpt.aapt.org
Naranjo Torres J., Montero G, Ríos V., García A. (2009). Implementación y Análisis de la Medida de Expansión Térmica Lineal, Revista Venezolana de Tecnología y Sociedad, pag 29-38, Enero-Julio, Vol 2 N° 1. pp. 29-38
Naranjo Torres J. (2006). Two Physical Phenomena in One Experiment, The Physics Teacher, pp 438-439, Vol. 44, October. Dirección electrónica: tpt.aapt.org
Sebastia, J.M., (1987). ¿Qué se pretende en los laboratorios de física universitaria?. Enseñanza de las Ciencias pp 196 – 204, Vol. 5 Nº 3.
Swartz C and Miner Th .(1997). Teaching Introductory Physics: A Sourcebook (American Institute of Physics,), p. 257
Thomsen, V. (1998). Response Time of a Thermometer, The Physics Teacher pag 540-541, Vol. 36, December
