SIMULACIÓN DE CINEMÁTICA LINEAL UTILIZANDO MODELLUS
INTRODUCCIÓN
Las simulaciones en física ofrecen a los estudiantes y profesores la posibilidad de tratar varios aspectos del modelo representado a través de la programación. Esto significa que las simulaciones rigen el comportamiento del sistema presentado en forma de animaciones o mediante gráficos y se puede manipular varios aspectos del modelo, ya que un evento, un objeto o un fenómeno son representados a través de la computadora. Es importante incluir en las clases de física, propuestas que utilicen recursos didácticos que ofrecen los nuevos medios. Es vertiginoso el desarrollo, que han experimentado en los últimos años la instrumentación tecnológica y de las tecnologías innovadoras y creadoras de solución de problemas, que beneficia a la comunidad educativa.
METODOLOGÍA
El uso del programa Modellus es disponible de libre acceso en el Internet y ayudaría a la construcción de modelos científicos en Física. El programa ofrece la posibilidad de interpretar y analizar los problemas, modificando variables independientes y las condiciones iniciales a cada una de las simulaciones. A las mismas se pueden acceder a diferentes ventanas donde se presentan situaciones físicas, por ejemplo la ventana del modelo matemático, la tabla, el gráfico, y cuadro de notas, que sirve para colocar el enunciado del problema. En la Figura se muestra cómo aparece en la pantalla el movimiento rectilíneo uniforme de un ensayo.
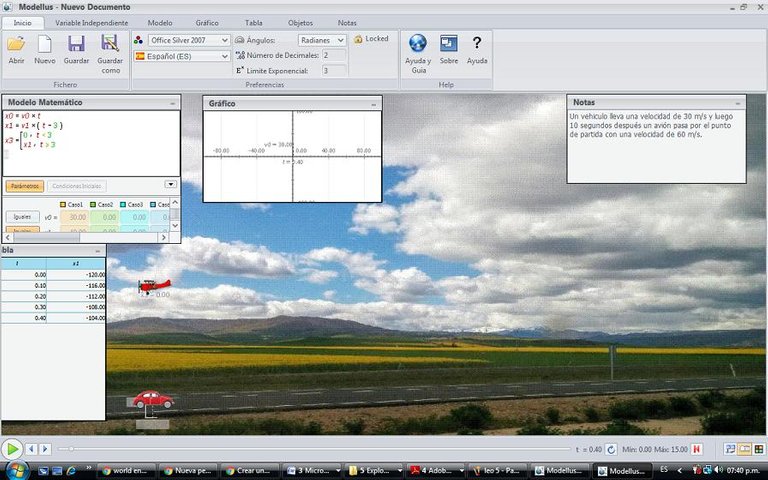
Los pasos que debe ser un usuario son los siguientes:
- Elegir el problema de física que se desea realizar. Un primer es recomendable escribir el problema en la ventana de notas, para poder visualizarlo en el software.
- Si deseas colocas una imagen de fondo para ver el problema un poco más real. Selecciona la opción de insertar imagen de fondo.
- En el menú del programa se selecciona la opción “Modelo” y se despliega una ventana, donde se escriben las ecuaciones matemáticas del modelo físico que se quiere representar. En este caso se debe expresar las ecuaciones de cinemática en una dimensión (eje horizontal)
- Al finalizar de escribir correctamente las ecuaciones, se procede a indicar los valores de los parámetros y las condiciones iniciales.
- Escoger las figuras que deseas y estén disponible en el software Modellus y que estén asociadas a al problema de física. (inserción de una partícula o de una imagen) se ofrecen en el margen izquierdo.
- Se selecciona la opción de reporte de tabla de datos, así como también y se requiere graficar, se puede lograr con el gráfica y se abrirá instantáneamente el comportamiento físico a estudiar.
- Se procede a ejecutar la animación en el botón Play que se encuentra en la parte inferior izquierda de la ventana.
- Para guardar el programa se selecciona la opción “Inicio” y se ejecuta el comando guardar para respaldar la información de la simulación creada
- Colocar las ecuaciones en el modelo matemático y escribir las condiciones del problema. (Los valores iniciales de posición y velocidad)
- Al crear la simulación, se puede convertir en una animación interactiva incorporando a la pantalla algunos cursores (encontramos el icono en el margen izquierdo) que indicarán el valor de magnitudes y permitirán su modificación cuando se esté ejecutando el programa. En este caso, introducimos un cursor para modificar sobre la marcha la aceleración y medidores directos de la posición y la velocidad. Este paso es opcional y es recomendable
- Hacer varias pruebas hasta que quede la simulación quede correcta
Problemas propuestos en Modellus
En esta sección se expone los ejercicios de cinemática lineal en dirección horizontal. Para esto, se coloco tres ensayos que se explican a continuación:
Simulación 1
Caso del problema del automóvil y del avión
La simulación 1 consiste en un sistema conformado por un automóvil y un avión que se mueven a velocidad constante, pero que están separados ambos a una distancia de 600 m, cuando ambos móviles llevan una velocidad respectivamente. La finalidad del problema es hallar mediante la simulación la distancia o punto de encuentro entre el avión y el automóvil. El enunciado del problema en física es dado como:
“Un vehículo lleva una velocidad de 25 m/s y luego 10 segundos después un avión pasa por el punto de partida o sistema de referencia con una velocidad de 60 m/s. En este sentido el avión esta a 600 m del punto de partida del vehículo. Con esta explicación, calcule el punto de encuentro de ambos móviles.”
Las ecuaciones que se usan son las de cinemática en dirección horizontal,
X=Xo+Vot+1/2at^2
V=Vo+at
Para este problema la aceleración es cero (a=0)
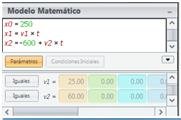
- Primero se escribe el modelo matemático y sus parámetros o datos:
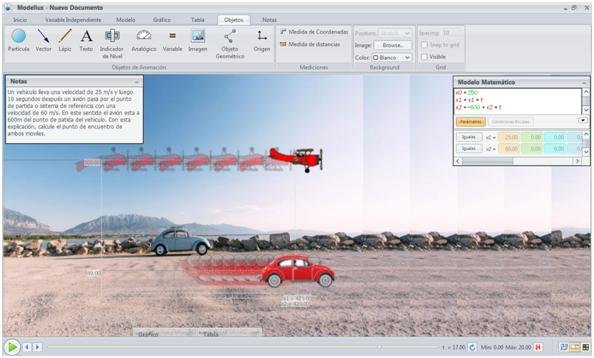
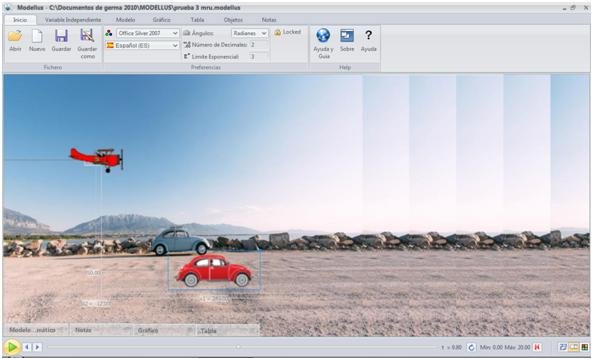
- Luego escoges los objetos que se van a mover: en este caso es el vehículo y el avión:
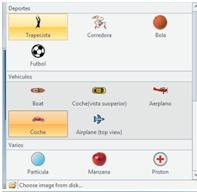
Aquí aparecen las figuras disponibles en el Modellus, sin embargo, se puede seleccionar otra imagen que se desees en la opción Choose imagen from disk, y seleccionar cual se con x1 y cual se moverá con x2. Para este caso x1 es el vehículo y x2 es el avión.
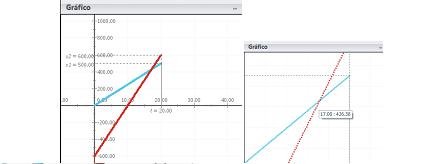
-Finalmente, puedes ver la gráfica instantánea de ambos móviles, además de visualizar el punto y el tiempo de encuentro. En este problema ambos se encuentran a 426 m del punto de partida del vehículo.
Simulación 2
Caso del problema de las locomotoras
La simulación 2 consiste en sistema conformado por dos locomotoras que se mueven a velocidad constante, pero que están separados ambos a una distancia de 600 m. La finalidad del problema es hallar mediante la simulación la distancia y el tiempo de encuentro entre ambas locomotoras. El problema es dado por el siguiente enunciado:
“Dos locomotoras están separadas una distancias de 8.5 Km. Sus velocidades son 100 Km/h y 120 Km/h respectivamente. En que tiempo se encontraran en la vía y a qué distancia desde el sistema de referencia del tren que viene de lado oeste.”
Se escribe el modelo:
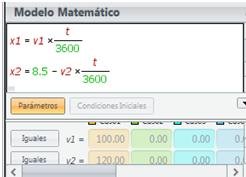
Se escoge los objetos (los ferrocarriles):
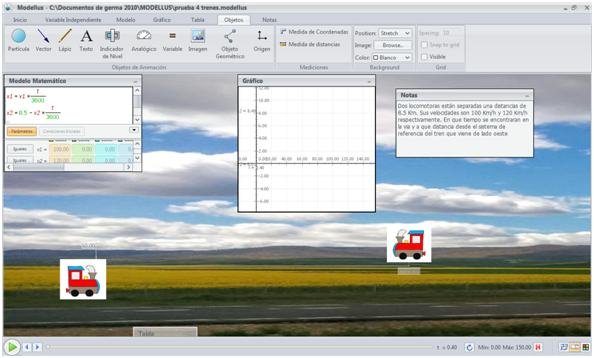
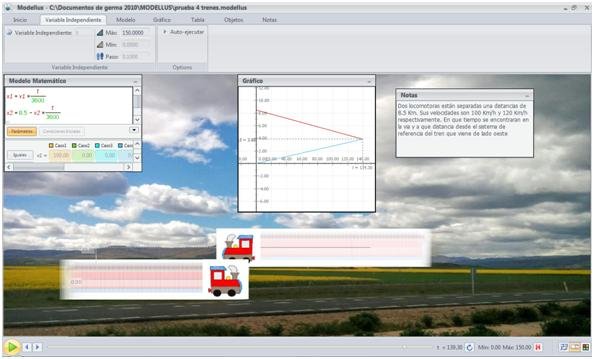
Y la gráfica se representa como:
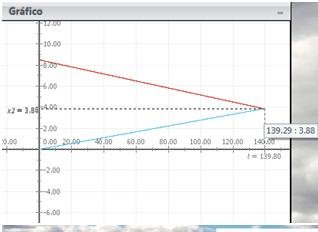
Se muestra un tiempo de t= 139,2 s y una posición de 3.88km
Simulación 3
Caso del problema de velocidades de animales
La simulación 3 consiste en un sistema conformado por el movimiento de un leopardo y de un venado. Ambos animales se mueven con una aceleración, generando un movimiento rectilíneo uniformemente acelerado. La finalidad del problema es determinar posiciones y tiempo en donde el leopardo captura al venado como su presa. El enunciado del problema en física es dado dos versiones:
Un leopardo acelera 3 m/s^2 de tal forma que en 20 s captura a su presa. Inicialmente él ésta a 4 m de una posición fija y su velocidad es de 20 m/s, entonces calcular la distancia a la cual alcanza a su presa con respecto a 4m del lado del leopardo.
Un leopardo acelera 3 m/s^2 y ve un venado a 600 m desde su posición inicial. Si el venado ve que el leopardo lo empieza a seguir, el empieza a correr 5 m/s^2, acelerando a 1.32 m/s^2. En qué punto el leopardo lo captura?
El modelo presentado para este problema es dado:
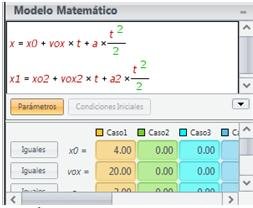
La simulación se observa como se representa en las figuras
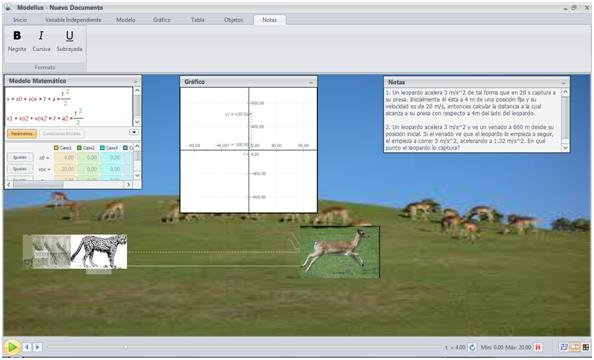
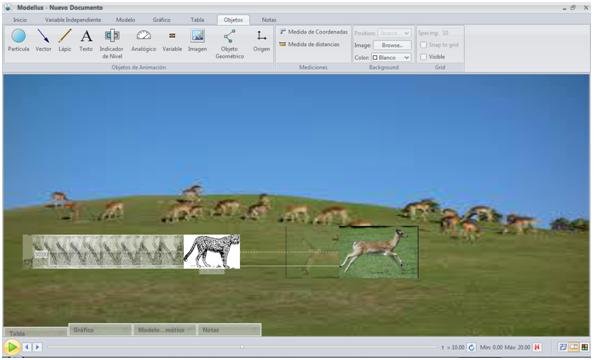
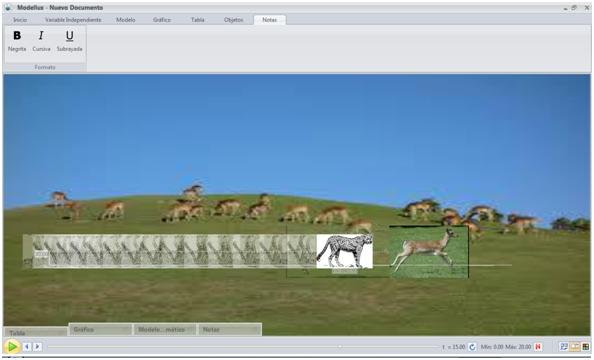
Las figuras insertadas son libre de uso:
leopardo
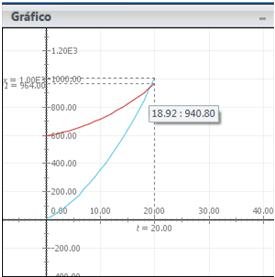
Finalmente, puedes ver la gráfica instantánea que determina el lugar de la captura y se puede visualizar el punto y el tiempo de encuentro. En este problema el leopardo alcanza y captura al venado a una distancia de 940.8 m del punto de partida y en un tiempo de 18.92 s.
CONCLUSIONES
La utilización de simulaciones con programas como Modellus, facilita al usuario poder realizar tareas de física cinemática, donde se puede llegar a ser más competentes en el estudio de situaciones físicas a través del modelado
Agradeciendo al grupo de steem-espanol con su etiqueta #steem-espanol
REFERENCIAS
Giancoli Douglas. Física. Principio con aplicaciones. Editorial Prentice Hall Mexico
Manuel Alonso Sánchez .Taller sobre animaciones Modellus de física. https://docplayer.es/7904031-Taller-sobre-animaciones-modellus-de-fisica.html
Tippens Paul (2011). Física. Conceptos y aplicaciones. Séptima edición. Editorial Mc Graw Hill
Zorrilla, Erica Gabriela. UNA EXPERIENCIA CON MODELLUS PARA EL ESTUDIO DE CINEMÁTICA EN EL NIVEL SECUNDARIO. Pixel-Bit. Revista de Medios y Educación, núm. 44, enero, 2014, pp. 7-17 Universidad de Sevilla Sevilla, España.
I upvoted your post.
Mabuhay, keep steeming.
@Filipino
Posted using https://Steeming.com condenser site.
Buen post @GermanMontero, bastante didáctico. La promoción de estas herramientas también es algo apropiado a la hora de educar. Por favor, revisa el enlace de la imagen del leopardo (está roto). Corrije todas menciones que haces a "stem-espanol" (algunas salen como steem-espanol'). Por último, debes especificar quién es el autor de todas las imágenes utilizadas. Si son tuyas, dilo explícitamente y si quieres especificar una licencia para ellas, mejor. Éxito.
Gracias @eniolw, por tu comentario. Todas las imágenes son propiedad de mi autoría @germanmontero, ya que se proporcionan del mismo programa Modellus. Por otro lado reconozco que hay un detalle en la letra adicional de stem-espanol. Estas cosas suelen suceder cuando las publicaciones no son continuas. En mis publicaciones están ese tipo de detalles escritos, para guardar respeto a las normas. Igualmente agradezco tus comentarios.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks @steemstem
Muy buen post amigo @germanmontero. Felicitaciones. Saludos.
Congratulations @germanmontero! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard: