El péndulo magnético
Hola de nuevo a todos, apreciados colegas y amigos de STEEMIT. De nuevo trayéndoles lo más destacado de mis archivos de Física Básica, en este caso el magnetismo. En Capítulos anteriores de la serie “La Física es Divertida” hemos estado discutiendo temas de nuestra vida donde el magnetismo es pilar fundamental. Entre estos hemos discutido temas tales como la rotación de La Tierra, las leyes de la magnetostática, polos magnéticos, la brújula, entre otros. Si se han perdido ésta Serie les invito a viajar por los enlaces:
Aunque parezca extraño, este Capítulo de “Misterios Magnéticos” está basado en una clase de mecánica dirigida a estudiantes de Ingeniería de la Universidad Rafael Urdaneta, en Maracaibo: “ondas mecánicas”. Aún cuando nos rodean los péndulos por todas partes, sorprendentemente pocos fueron capaces de describir un péndulo simple y dar ejemplos de la cotidianidad.
No hemos percibido que cuando sopla el viento, las hojas de un árbol y los cables colgando en los postes realizando movimientos de vaivén, tal como el péndulo. Un trapecista se impulsa como un péndulo para salir del trapecio. El corazón es una bomba mecánica que impulsa la sangre por nuestro cuerpo, en un movimiento de ida y vuelta como un péndulo. Los relojes mecánicos son péndulos.
El problema se complica cuando involucramos a los campos magnéticos. Estamos rodeados de campos magnéticos por todas partes. Es inevitable. La Tierra tiene un campo magnético de 0.5 Gauss, suficiente para orientar la aguja de una brújula, y guiar a las aves en su travesía a través del planeta. Los insectos también se orientan siguiendo el campo magnético terrestre. Ciertas bacterias se desarrollan o mueren dependiendo de la intensidad y frecuencia del campo magnético.
Ahora bien, los planetas giran alrededor del Sol tal como lo hace un péndulo alrededor de un punto fijo. Pero también giran alrededor de su propio eje, en movimiento de rotación. Un péndulo simple bajo la acción de la gravedad no rota. Entonces surgen algunas cuestiones,
Este trabajo es una combinación de mecánica clásica y electromagnetismo, cuyo objetivo es responder estas y otras cuestiones relacionadas con el péndulo. Para responder estas preguntas debemos observar y experimentar un poco. Les mostraré que podemos resolver problemas científicos de nuestro entorno sin equipamientos complejos y costosos, y sin tener gran experiencia en física. En este trabajo les propongo un paseo a través del movimiento de un péndulo magnético hecho en casa.
Con la finalidad de hacer este proyecto más interactivo, les agradezco dejarme sus inquietudes y preguntas en un REPLAY, y así darles respuesta.
Para más información sobre este tema y otros relacionados con Ciencia, Física y Tecnología, les invito visitar mis sitios:
Física del péndulo
Desde el punto de vista coloquial o cotidiano, un péndulo es cualquier objeto que se mueve en un movimiento de vaivén. Formalmente, un péndulo es un cuerpo de masa m suspendida de un punto fijo, O, por medio de una cuerda de longitud L y masa despreciable, y que describe un movimiento oscilatorio alrededor de un eje que pasa por el punto O. En todos los cursos de Física básica se resuelve el problema del péndulo simple donde no hay fricción del medio. Sin embargo aquí nuestro péndulo oscila en un medio real con constante de viscosidad β, tal y como se muestra en la Figura 1,
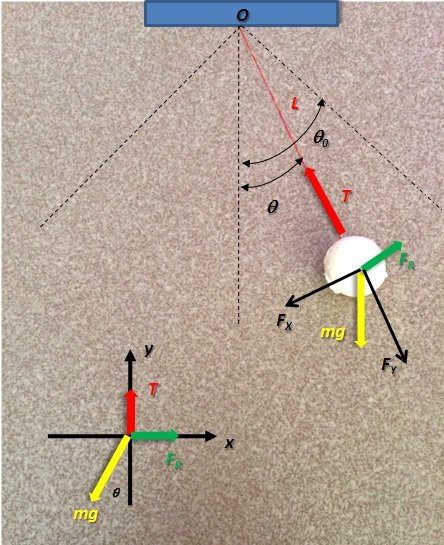
Si el péndulo es llevado a una posición inicial θ0 este se moverá a lo largo de un arco de circunferencia s(t) = Rθ(t). Resolviendo el diagrama de fuerzas de la Figura 1, se obtiene la conocida ecuación del péndulo amortiguado,

donde γ= β/2mL es la constante de amortiguamiento y (g/L)-1/2 la frecuencia natural del péndulo. Esta es una ecuación no-lineal cuyas soluciones son integrales elípticas. Sin embargo, debido al amortiguamiento del medio, el ángulo de oscilación decaerá rápidamente y el péndulo ejecutará oscilaciones pequeñas. En ese caso θ∼0, y la ecuación 1 tendrá la forma más simple,


θ0 y a son constantes que dependen de las condiciones iniciales. Esto corresponde a una oscilación de frecuencia angular ω12=ω02 - γ2 y amplitud θ0 exp(-γt). Estas oscilaciones tienen período,

La viscosidad del medio incrementa el período de la oscilación. Si g=0, entonces el período corresponde al del péndulo simple,

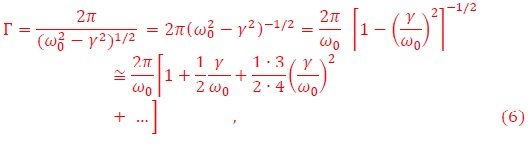
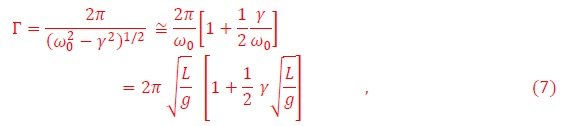

Si el péndulo oscila en presencia de una fuerza externa f(t), entonces la ecuación del movimiento es,

La solución de esta ecuación depende de la forma de la fuerza. En los cursos de Física básica universitarios se estudia el caso cuando la fuerza externa es periódica, es decir,


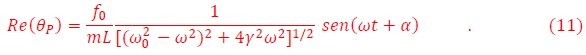
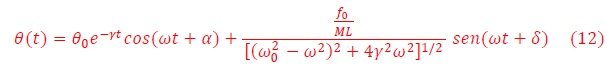
El péndulo magnético
Antes de resolver el problema del péndulo magnético, es necesario revisar la dinámica de un dipolo magnético en un campo externo. Definimos un dipolo magnético, p, a un sistema formado por dos polos magnéticos (norte-sur) opuestos inherentes e inseparables: a) una barra magnetizada, b) un anillo metálico, c) cualquier material ferromagnético. El dipolo se orienta a lo largo de la línea imaginaria que une ambos polos, y a su vez genera un campo magnético en cualquier punto del espacio.
Este campo no es homogéneo sino más bien depende del punto de medición, es decir es inhomogéneo. Supongamos que colocamos una barra de hierro en el campo producido por un imán, como se muestra en la Figura 2.
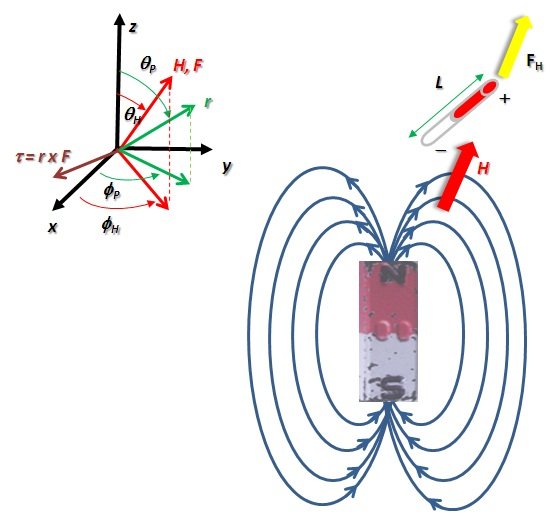 )
)Figura 2. Barra magnetizada en presencia de un campo magnético producido por un imán (Figura original propiedad del Autor)






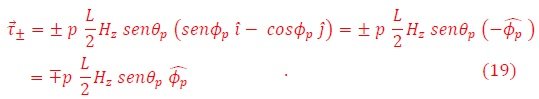
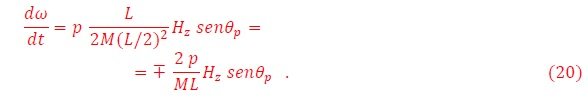

La barra de hierro se magnetiza en presencia del campo magnético del imán, H, formando un dipolo magnético de intensidad p=m/L, donde m es el momento magnético. La fuerza magnética que actúa sobre la barra es,

Aquí (+/-) se refiere al polo (N/S) respectivamente. El centro de masa (CM) de la barra es atraído hacia el imán en un movimiento gobernado por las ecuaciones de movimiento,


La solución de este sistema de ecuaciones involucra álgebras tediosas. Se nota sin embargo, la presencia de las derivadas temporales de θP y фP, es decir, existen torques inducidos por el campo sobre el dipolo. Entonces, en vez de resolver el sistema (15) utilizaremos la técnica del torque para analizar la dinámica del sistema. La fuerza (13) induce sobre la barra un torque magnético,


En el caso más simple del campo magnético orientado a lo largo del eje “z” (Hx=Hy=0; H=Hz), el torque ejercido sobre la barra magnética está contenido en el plano (x, y) (ver Figura 2) y satisface la expresión,

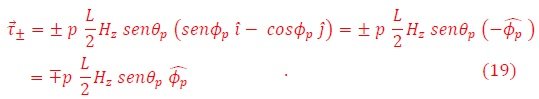
Este es un giro en el plano azimutal, es decir alrededor del eje “z”, adicionalmente a la traslación del centro de masa a lo largo de “z”. Utilizando las relaciones entre el torque y el momentum angular τ=dL/dt, y la expresión del momentum de un cuerpo rígido L=MR2ω, obtenemos la ecuación de la frecuencia del giro,
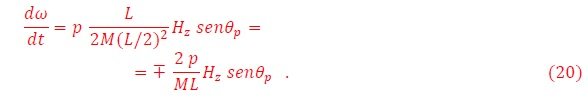

Mayor el campo, más rápido gira el objeto magnetizado. Con esto entonces hemos caracterizado el movimiento de una barra magnética en presencia de un campo externo. Lo mismo ocurre si en vez de una barra magnetizada colocamos una esfera magnetizada: rotará alrededor de su eje.
A continuación abordaremos el problema del péndulo magnético. Dos casos podemos analizar: a) imán estático; b) imán en movimiento periódico.
Campo estático.
Consideremos ahora un péndulo magnético de masa M, oscilando en presencia del campo estático producido por un imán, como en la Figura 3. La masa está conectada a un punto fijo mediante una cuerda inelástica de masa despreciable y el campo en la dirección “z”.
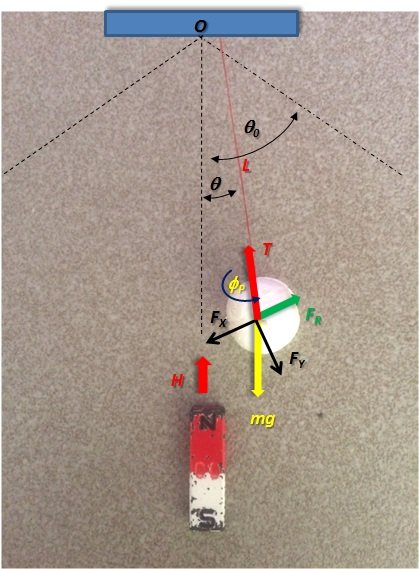
Figura 3. Péndulo magnético oscilando en presencia de un campo magnético estático (Figura propiedad del Autor).
El problema es similar al del objeto magnetizado, pero con la traslación del CM a lo largo del arco de circunferencia Lθ. Resolviendo el diagrama de fuerzas de la Figura 3 en el régimen de oscilaciones pequeñas se obtiene la ecuación simplificada para el CM,
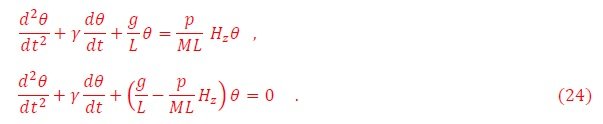
Esta es la ecuación de un péndulo de frecuencia natural,

que oscila con frecuencia ω12= ωH2-(g/L)2. El campo magnético disminuye la frecuencia natural del péndulo, y la frecuencia de las oscilaciones. El período entonces aumenta de acuerdo a la relación,


A diferencia del péndulo simple, el periodo del péndulo magnético depende de la masa. Ahora bien, las ecuaciones (18) y (19) predicen que el campo magnético ejerce un torque que induce una rotación del objeto magnetizado alrededor de su propio eje. Entonces tenemos la ecuación del torque,

En el régimen de oscilaciones pequeñas θP∼ θ. El torque se invierte alternadamente de un sentido al otro, produciendo una oscilación de período determinado por la ecuación (23),

Nuestro análisis es muy simple y no se aplica al caso más general, pero nos permite representar razonablemente la dinámica de un péndulo magnético.
Campo variable
Consideremos ahora que el campo es producido por un imán que se mueve lentamente en un movimiento circular de frecuencia constante, ω, como en el esquema de la Figura 4.
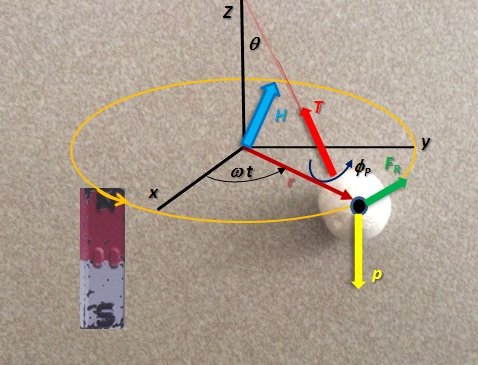
Figura 4. Péndulo magnético en presencia de un campo variable. (Figura propiedad del Autor)
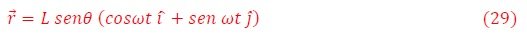
La fuerza magnética y la cuerda se orientan formando un ángulo θ con respecto a la vertical. El peso está en la vertical y la fricción tangente a la trayectoria del péndulo en el plano horizontal. Resolviendo el diagrama de fuerzas de la Figura 4, se obtiene que las fuerzas que actúan sobre el péndulo son,

con una fuerza neta,

donde βv es la fuerza de fricción. Esta fuerza produce un torque sobre el péndulo dado por el producto vectorial (16), cuyas componentes son,

Sustituyendo las ecuaciones (29)-(34), obtenemos, en coordenadas esféricas la ecuación del torque,

El campo variable produce una precesión en el plano horizontal y una oscilación transversal a lo largo de la trayectoria del péndulo. Cuando el péndulo relaja por acción de la fricción, el péndulo decae en el régimen de pequeñas oscilaciones. En éste régimen, el torque es,
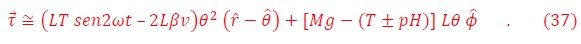
El segundo término es mucho mayor que el primero y solo depende de la intensidad del campo. Entonces finalmente el movimiento del péndulo magnético es predominantemente una oscilación alrededor del eje vertical,

A este tipo de péndulo también se acostumbra denominarlo “péndulo esférico”. La Tierra es un péndulo esférico gigante.
Demostración: péndulo magnético
Materiales y procedimientos
En esta sección les presentaré una serie de demostraciones caseras que ilustran el movimiento de un péndulo magnético. Para esto necesitaremos básicamente los materiales y elementos que se muestran en la Figura 5. Luego que tengas todos los materiales a la mano, construye las estructuras como aparecen en la Figura 6. La base graduada del imán es opcional pero te facilitará la visualización del movimiento. Si no consigues una la puedes diseñar tu mismo. Para el péndulo une un trozo de hilo a la cabeza del alfiler e insértalo en la esfera de anime. Con el alambre construye un anillo y colócalo justo en el ecuador de la esfera de anime. Esto es para estabilizar la rotación del péndulo. Seguidamente amarra el extremo libre del hilo en el punto medio de la base de la barra. Apoya los extremos de la barra sobre un par de botellas o envases para permitir el libre movimiento. Pega el disco graduado al envase de plástico para construir una base para el imán y colócalo encima.

Figura 5. Materiales utilizados en nuestras demostraciones (Propiedad del Autor. Fotografías tomadas con un dispositico iPhone 5s/12 Mpixels).

Figura 6. Montajes experimentales para las demostraciones del péndulo magnético (Propiedad del Autor. Fotografías tomadas con un dispositico iPhone 5s/12 Mpixels).
a) Campo estático. Para producir un campo magnético estático simplemente necesitas un imán en reposo. Una vez que tengas tu péndulo, déjalo reposar hasta que alcance estado de reposo. Es importante que el plano horizontal esté nivelado ya que cualquier inclinación afectará el movimiento del péndulo. Finalmente, recomiendo colocar un anillo de alambre a lo largo del ecuador de la esfera. Esto con la finalidad de amplificar el movimiento rotacional del péndulo. Ahora, coloca el imán en la palma de tu mano y acércalo lentamente al péndulo hasta que éste comience a oscilar.
b) Campo variable. La manera más simple de producir un campo magnético variable es desplazar un imán en movimiento periódico lento. Repite los pasos anteriores pero en vez del imán en reposo, muévelo lentamente siguiendo una trayectoria circular, y observa lo que ocurre. Este es el origen de la rotación de un planeta alrededor del Sol.
Comentarios finales
Las fuerzas magnéticas son fuerzas invisibles que llenan todo el espacio que nos rodea, produciendo efectos que pueden parecer extraños para nosotros. Los campos magnéticos son el producto de las cargas en movimiento, o corrientes eléctricas. Si estas corrientes son internas, entonces, el material está magnetizado: un imán. Todos los organismos vivos han evolucionado para adaptarse a la acción de estos campos. Gracias a los campos magnéticos las aves e insectos se pueden orientar.
Sin el campo magnético del Sol la Tierra no rotaria sobre su propio eje, y por lo tanto, no existiría el día y la noche. Tendríamos un planeta sobrecalentado en un lado y sobre enfriado en el otro: en consecuencia no existiría la vida en el planeta. De hecho, La Tierra y demás planetas del sistema solar son “péndulos esféricos”. Con demostraciones sencillas estudiamos la dinámica de estos péndulos, y reproducimos el movimiento de un planeta alrededor del Sol.
Antes de despedirme, me gustaría llamar la atención de la comunidad de docentes tanto a nivel medio como universitario, para que consideren incorporar en sus actividades docentes la discusión de estos problemas cotidianos, donde las leyes y principios de la física son la base fundamental.
Lecturas sugeridas sobre física divertida y otras curiosidades de física:
1. Neil Ardley, 101 grandes experimentos. La ciencia paso a paso (Ediciones B, 1997).
2. Isabel Amato y Christian Arnould, 80 experimentos para hacer en casa. Respuestas a los curiosos (Ediciones B, Barcelona, 1992).
3. Fundación Thomas Alva Edison, Experimentos fáciles e increíbles (Martínez Roca, Barcelona, 1993).
4. Judith Hann, Guía práctica ilustrada para los amantes de la ciencia (Blume, Barcelona, 1981).
5. Antonella Meiani, El gran libro de los experimentos (San Pablo, Madrid, 2000).
6. Yakov I. Perelman, Física recreativa (Eds. Martínez Roca, Barcelona, 1971).
7. Yakov I. Perelman, Problemas y experimentos recreativos (Mir, Moscú, 1975).
8. Gaston Tissandier, Recreaciones científicas, o la física y la química sin aparatos de laboratorio y sólo por los juegos de la infancia (Alta Fulla, Barcelona, 1981).
9. Tom Tit, La ciencia divertida (José J. de Olañeta, Palma de Mallorca, 1992).
10. Alejandra Vallejo-Nágera, Ciencia mágica. Experimentos asombrosos para genios curiosos (Martínez Roca, Barcelona, 1999).
11. Janice P. Van Cleave, Física para niños y jóvenes. 101 experimentos super divertidos (Limusa, México, 1997).
Lecturas recomendadas sobre la física del péndulo y magnetismo
12. Keith R. Symon. Mechanics (Addison Wesley Pubs, USA, 1971).
13. Marcelo Alonso y Edward Finn, Mecánica (Addison Wesley Iberoamericana, México, 1986).
14. Frank S. Crawford, Ondas. Berkeley Physics Course, Vol. 3 (Editorial Reverté, México, 1979) /div>
15. E. W. Lee, Magnetism: an introductory survey, DOVER Pub. Inc, NY (1970).
16. Guillermo Heyaca Verela, Energía de los Campos Magnéticos, Eds. Nueva Librería, Buenos Aires (1980).
17. Nicola Spaldin, Magnetic Materials: Fundamentals and Device Applications, Cambrigde University Press (2003)
18. Rebecca Carmi, Amazing Magnetism: Magic School Bus Chapter # 12, Scholastic Inc. (2001)
Excelente publicación @jfermin70. Se ve bien trabajado y desarrollado el contenido, y soportado por ecuaciones que dominan y rigen el comportamiento de la cinemática experimental explicada muy bien en este artículo referente a los misterios magnéticos que creo queda al descubierto en tu explicación del péndulo magnético. Gracias por compartir este excelente aporte con nosotros. Saludos
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Entra aquí para más información sobre nuestro trail.Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Congratulations @jfermin70! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Saludos estimado @jfermin70. Excelente trabajo y una impecable presentación del péndulo magnético. Mis felicitaciones.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Hi @jfermin70!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Congratulations @jfermin70! You received a personal award!
Click here to view your Board
Hello @jfermin70! This is a friendly reminder that you have 3000 Partiko Points unclaimed in your Partiko account!
Partiko is a fast and beautiful mobile app for Steem, and it’s the most popular Steem mobile app out there! Download Partiko using the link below and login using SteemConnect to claim your 3000 Partiko points! You can easily convert them into Steem token!
https://partiko.app/referral/partiko