Hola amigos de steemit
Hoy quiero compartir con ustedes una preocupación o mejor dicho una curiosidad que siempre he tenido en lo que refiere a conocer el método para conocer las posibles cifras que se obtienen para hacer permutaciones, cuando estaba mas chico, mi abuela casi a diario me enviaba a la agencia para jugarse un número en la lotería, siempre me decía
- Mijo haceme el favor de ir a la agencia y jugate la permuta de tal numero.
El numero generalmente era deducido de un sueño, pues en la cultura popular que hay en mi región soñar con acontecimientos específicos es señal de que puedan darse buenas o malas noticias dependiendo del sueño que se considera como un prefacio, pero eso es otro tema.
Mi inquietud me llevo a encontrar respuestas en una teoría matemática básica, llamada Teoría Combinatoria, es un contenido que explica el método que se usa para realizar las permutaciones. Para llegar a tal punto mostrare unos conceptos previos mas simples que daran mayor comprensión y luz acerca del tema.
Fuente
Elementos de la teoría combinatoria
En aritmética, el concepto del número natural se llega a partir del de conjunto, sin tomar en cuenta la naturaleza de los elementos que lo forman, ni el orden de ubicación en el que se encuentran. Por ejemplo, el número 6 representa en forma abstracta todos los conjuntos de seres u objetos que están coordinables con el A, B, C, D, F, independientemente de la naturaleza y el orden de los elementos de dichos conjuntos.
Por el contrario, en la teoría combinatoria se consideran en los conjuntos el orden de colocación de sus elementos y las diversas maneras de agruparlos. El ejemplo más simple está dado por: Considere las cifras 1,2,3 y 4, uno puede comprender fácilmente que es posible formar muchos números con estos dígitos, 123, 234, 341, etc., diremos que dos de ellos son diferente en las siguientes condiciones:
- Cuando tienen algunas de las cifras desiguales
- Cuando aun teniendo las mismas cifras, estas se encuentran en diferente orden.
Ahora según estas condiciones, se presentan 3 casos, descritos como variación, permutación y combinación.
Variaciones
Entonces las condiciones descritas presentan un primer problema que generalmente se llama Variación. El número de elementos elegidos del total dado, para formar los diferentes grupos expresa el orden de la variación, así los diferentes números de tres cifras que pueden formarse con los cuatro mencionados anteriormente, constituyen las variaciones de orden 3 con 4 elementos, o simplemente variaciones ternarias de 4 elementos, y se expresan mediante la notación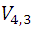
. En general, el número de variaciones de orden n que pueden formarse con m elementos con m> n está designado por 
(1).
Por lo tanto, las variaciones se definen de la siguiente manera:
Dado m objetos, se denomina variaciones de orden n con m> n, a los grupos que pueden formarse tomando n de esos m elementos que nos dan, de modo que dos cualesquiera de los grupos se consideren diferentes cuando: a) difieren en algún elemento; b) si tienen los mismos elementos, se colocan en un orden diferente
Formación de variaciones
Las variaciones con un cierto número de elementos dados pueden formarse sucesivamente por un método uniforme, que consiste en agregar a cada variación de un orden determinado cada uno de los elementos que no aparecen en él. Para ver esto, continuamos con nuestro sencillo ejemplo:
Queremos determinar las variaciones que se pueden formar con cuatro elementos a, b, c y d, para ello procedemos de la siguiente manera, para la variación del primer orden, está claro que
Para las variaciones binarias o tomadas de dos a dos, se obtienen de las anteriores, escribiendo al lado de ellas, cada uno de los elementos restantes como sigue:
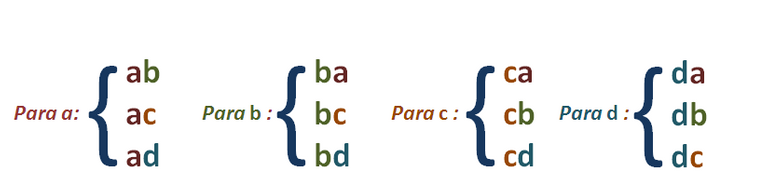
Como el primer lugar de la variación binaria puede ser ocupado por cualquiera de los cuatro elementos dados: a, b, c, d y una vez que se coloca uno de ellos, hay tres elementos disponibles para ocupar el segundo lugar, para lo cual es fácil de entender que el total es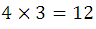 
de variaciones binarias de los cuatro elementos dados.
Para las variaciones tomadas de tres a tres, se deducen de los procedimientos binarios de una manera similar, es decir, escribiendo cada uno de los elementos restantes después de estos últimos, así:
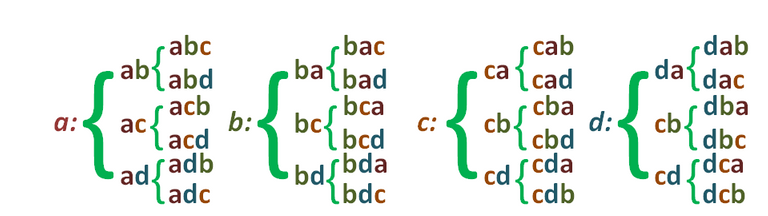
Como en este caso, los elementos restantes son dos para cada variación binaria, resultan, como se puede observar, dos ternarios, el número total de estos es entonces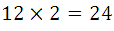 
.
Finalmente las variaciones cuaternarias, o tomadas de cuatro a cuatro, se deducen de manera similar y son todas aquellas ternarias que añaden la última letra, por lo que también obtendremos 24 variaciones.
Desde un punto de vista general, podemos decir que el número de variaciones de orden n que pueden formarse con m elementos (n <m) se obtiene multiplicando las de orden n-1 por el número de elementos restantes, por lo que este último número es dado por la expresión:
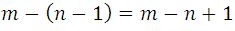
Simbólicamente y considerando la expresión de variaciones, la propiedad anterior se puede expresar:
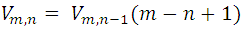
Por ejemplo, la expresión anterior se usa de la siguiente manera:
Ahora para calcular una variación 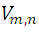sabemos que el número de variaciones de m elementos tomados uno por uno es m, de esta forma podemos hacer uso de:
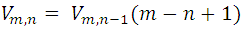
con n = 1,2,3, ..., n, sucesivos, tienes que:
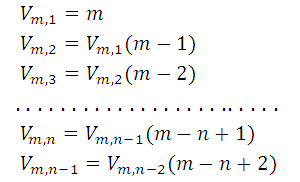
Si multiplicamos estas desigualdades miembro a miembro, y simplificamos los factores comunes, es claro ver:
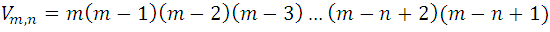
Como este resultado es general, entonces podemos decir:
El número 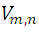, es decir, el número de variaciones de m elementos tomados n a n, es igual al producto de n factores consecutivos y decrecientes a partir de m.
Entonces, como pueden ver, esta es la fórmula para conocer las variaciones, para mayor claridad denotemos un ejemplo:
- En una habitación donde hay ocho asientos, entran cinco personas, ¿de cuántas maneras pueden sentarse?
La pregunta anterior claramente es un problema de variación porque al cambiar el orden de colocación de las personas en los asientos, los grupos se consideran diferentes. Entonces se tiene:
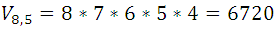
El número anterior representa el número de personas que pueden sentarse. Veamos otro problema que merece más álgebra:
- Si
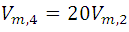, calculemos el valor de m
considerando la expresión de 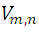para 
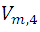y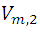 
podemos escribir:
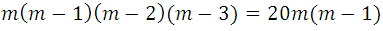
Eliminando los factores comunes de ambos miembros, y creamos el producto:
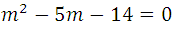
Resolviendo el polinomio de segundo grado:
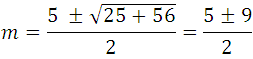
De donde obtenemos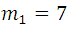 
, que es el valor buscado.
Permutaciones
Aclarado lo que significa variación, la permutacion representa un caso particular del punto expilcado, es decir, es una variacion de m elementos tomados m a m. Así por ejemplo las permutaciones de dos elementos , a y b, son ab y ba; para a,b y c son: abc, acb, bca, bac, cab, de manera que la permutacion de m elementos son las distintas maneras como pueden ordenarse todos ellos y se expresa como sigue:
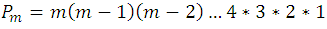
por ejemplo la permutacion de 5 y 6 elementos sera de la siguiente forma:
Asi de simple son las permutaciones, la formutila anterior solo dice el numero de las distintas formaciones, mas no da información sobre cuales podría ser cada formación,a pesar de ser un tema básico conduce a otros temas mas complejos que nos permite calcular por ejemplo los coeficientes de _polinomio Newton*_ , tales conceptos serán discutidos más adelante en la siguiente publicación, espero que esta publicación sea de su interés y beneficio. Gracias por leerme y apoyarme.
Bibliografia :
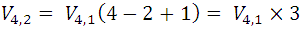
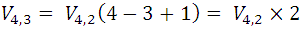
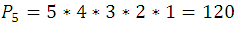
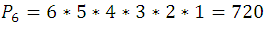
Hola tu artículo tiene potencial, pero nos gustaría saber quien eres..por eso deberías realizar un preséntate a ti mismo y así verificar tu identidad
hola @carloserp-2000 esta es mi introduccion, la hice hace un mes. No se si es necesario que realice otra, sin embargo si es necesario que lo haga me avisas y la realizo con mucho gusto