Hola amigos steemianos
Continuando con el estudio de los determinantes y los métodos utilizados para el desarrollo de los mismos, expongo en este post el repaso de algunas técnicas conocidas y las propiedades mas importante en la resolución de esta herramienta matemática. Considerando el concepto de los determinantes, observemos el siguiente arreglo de términos:
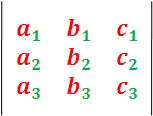
Imagen realizada por mi persona @juancmz
El desarrollo muy bien lo podemos obtener por las reglas de Cramer, pero existe también otros métodos muy conocidos como la Regla de Sarrus, la cual consiste en agregar ordenadamente las dos primeras filas o las dos primeras columnas y formar los productos como lo expresan las flechas del siguiente diagrama:
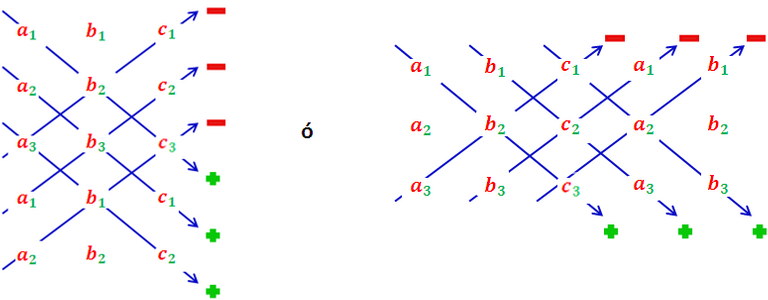
Imagen realizada por mi persona @juancmz
De la ilustración anterior, queda claro el mecanismo por el cual se trabaja en la Regla de Sarrus,técnica que nos permite desarrollar determinantes de tercer orden de una forma simple y efectiva, ya que consiste en multiplicar, sumar y restar en el orden mostrado anteriormente, como por ejemplo:
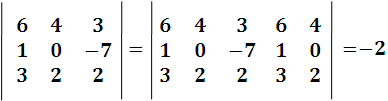
Imagen realizada por mi persona @juancmz
Menores complementarios
Los menores complementarios es una forma de simplificar el desarrollo de los determinantes, para tal efecto consideremos lo siguiente:
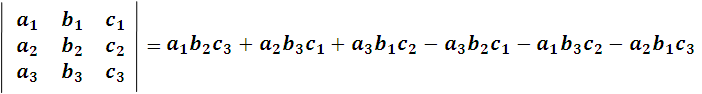
Imagen realizada por mi persona @juancmz
Si en el desarrollo sacamos por factor común a1, a2 y a3, podemos agrupar los términos de la siguiente manera:
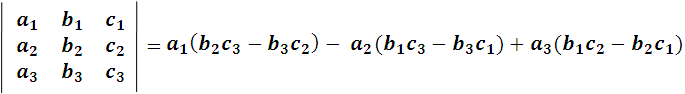
Imagen realizada por mi persona @juancmz
Si observamos detalladamente los productos internos de cada factor común, se puede reescribir lo anterior como:
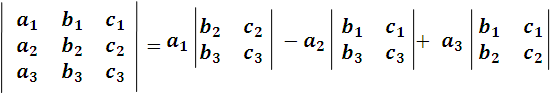
Imagen realizada por mi persona @juancmz
Notemos que los determinantes de segundo orden que multiplican a cada uno de los elementos a1, a2 y a3 son el resultado de suprimir en el determinante dado la fila y la columna que se cruza en dichos elementos, formando estos determinantes denominados menores complementarios de los elementos seleccionados así tenemos:
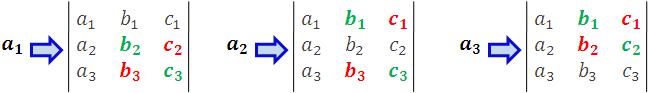
Imagen realizada por mi persona @juancmz
Posteriormente para determinar el signo de los elementos, se toma la suma de los números que indican la fila y la columna del elemento correspondiente sea par o impar. Así, el primer término del desarrollo mostrado anteriormente es positivo, porque el elemento a1 pertenece a la primera fila y a la primera columna (1+1 =2) lo que corresponde a un número par, en cambio, el segundo término es negativo, porque a2 pertenece a la primera columna y a la segunda fila (1+2=3), lo que es un número impar, el último término es positivo, pues a3 esta en la primera columna y la tercera fila 1+3= 4 lo cual corresponde a un número par.
El procedimiento expuesto aplica para cualquier elemento del determinante, por ejemplo si desarrollamos el determinante tomando los elementos de la segunda columna, resulta:
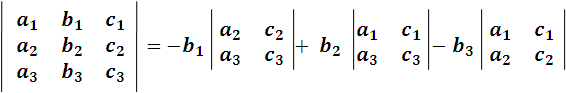
Imagen realizada por mi persona @juancmz
En resumen, podemos decir:
Para desarrollar un determinante por los elementos de una fila o columna cualquiera se escriben los productos de dichos elementos por sus menores correspondientes, dando a cada término el signo + o -, según que la suma de los números que indican los lugares de la fila y columna del elemento respectivo sea par o impar.
Conocidos los métodos mas comunes y fáciles de aplicar para el desarrollo de determinantes de tercer orden, surgen una pregunta muy interesante ¿cómo desarrollar determinantes de orden superior o de cualquier orden?, la respuesta a esta incógnita amerita estudiar los determinantes de forma general.
Generalización de los determinantes
Para obtener el desarrollo de determinantes de orden superior al tercer, es conveniente aclarar los siguientes conceptos.
Inversiones de una permutación.
Hace tiempo realice una publicación hablando del significado de las permutaciones, en esta sección volvemos a ver su utilidad aplicado a la resolución de determinantes, entonces consideremos m objetos entre los que se establece un orden de sucesión, por ejemplo, el alfabético si se trata de letras, o el de la sucesión natural para los números, o en este caso para una letra con índice numérico, en el cual llamaremos permutación principal a aquella en que los elementos están en un orden inicial, en otra permutación cualquiera se dice que dos elementos forman sucesión cuando, prescindiendo de los restantes, están en el mismo orden que en la permutación principal y que forman inversión si aparecen en orden contrario.
Así por ejemplo tenemos a1,a2,a3,a4 como una permutación principal, en a3,a2,a1,a4 se forman las siguientes inversiones, a3 con a2, a3 con a1 y a2 con a1. Se determinan las inversiones de una permutación comparando cada elemento con todos los que le siguen, de esta manera diremos que una permutación es par o impar , según sea par o impar el número de sus inversiones, por lo tanto la permutación anterior es impar, por ser impar el número de sus inversiones.
Desarrollo general de un determinante
Para una mayor compresión de este procedimiento observemos de nuevo el determinante de tercer orden:
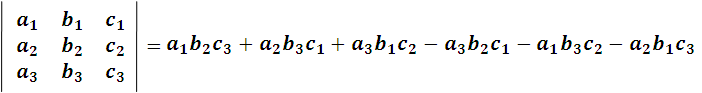
Imagen realizada por mi persona @juancmz
Notemos que las letras conservan el orden que en la diagonal principal, pero la permutación ocurre en los subíndices, con todas las inversiones posible que se pueden formar con los números 1,2 y 3, es decir,
Las permutaciones con que los subíndices aparecen en los términos positivos son: 123, 231, 312, los cuales presentan 0, 2 y 2 inversiones respectivamente, en cambio las permutaciones de los subíndices en los términos negativos son: 321, 132 y 213, las cuales presenta inversiones 3, 1 y 1 respectivamente, por tanto podemos asumir que los términos positivos del desarrollo son aquellos cuyo número de inversiones es par, mientras que los términos negativos son aquellos con número de inversión impar.
)
Determinante de orden n
Entendido lo anterior nosotros podemos considerar un determinante de orden n, con n elementos dispuestos en n columnas y en n filas, cuya diagonal principal esta constituida por a1, b2, c3, d4 ... kn. La suma algebraica de todos los posibles productos de los n factores se realiza aplicando la siguiente regla:
"El desarrollo de un determinante de orden n es igual a la suma algebraica de los términos que se obtienen permutando en la diagonal principal a1, b2, c3, d4 ... kn los subíndices de las letras de todas las maneras posibles, y dando a cada término el signo + o -, según que el número de inversiones que presenten sus subíndices sea par o impar."
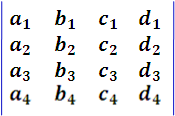
Imagen realizada por mi persona @juancmz
Así por ejemplo, para desarrollar el determinante de cuarto orden, debemos formar todas las permutaciones de los subíndices 1, 2, 3 y 4. De esta manera los términos resultantes serán los formados por los índices 1234, 1243, . . . , 3241, . . . ,4321 los cuales determinan el signo según el número de las conversiones realizadas, por otro lado es claro que el número total de términos viene dado por 4! = 1x2x3x4 =24.
Propiedades de los determinantes
Cada producto en el desarrollo de los determinantes contiene un elemento, y sólo uno de cada fila y otro de cada columna, esto nos permite entender mejor las siguientes propiedades:
a. Un determinante es nulo si son nulos todos los elementos de una fila o de una columna. Para verificar esta propiedad basta con desarrollar dicho determinante con relación a los elementos de dicha fila o columna, mediante el método de los menores complementarios

Imagen realizada por mi persona @juancmz
b. Producto por un número: Si se multiplican todos los elementos de una fila o columna por un número m, el determinante queda multiplicado por m.
Es fácil ver esto con un ejemplo:
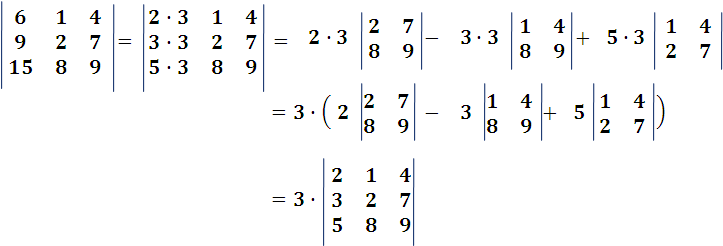
Imagen realizada por mi persona @juancmz
Al desarrollar por los elementos de dicha columna o fila quedan multiplicados por m los n términos y, por consiguiente, el determinante.
c. Cambio de filas por columnas. El valor de un determinante no se altera cuando se cambian sus filas por columnas.
Así, por ejemplo se tiene:
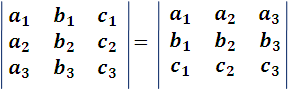
Imagen realizada por mi persona @juancmz
Ambos determinantes tienen la misma diagonal principal, luego se obtendrán iguales desarrollos, por componerse de idénticos términos, aplicando el procedimiento de permutar los subíndices de los elementos de dicha diagonal.
d. Suma de determinantes. Si los elementos de una fila (o columna ) de un determinante son polinomios de n términos, el determinante puede descomponerse en suma de n determinantes.
Por ejemplo, se tiene:
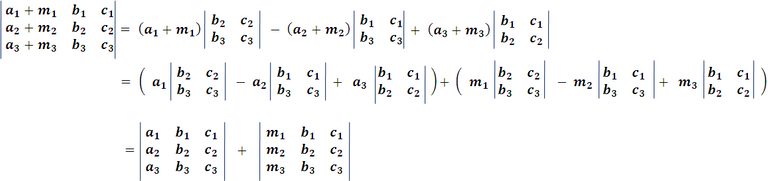
Imagen realizada por mi persona @juancmz
De manera que la suma de varios determinantes que sólo difieren en una fila o columna, es otro determinante que tiene dicha fila o columna formada por la suma de los elementos de aquéllas, y todas las demás idénticas a las de los dados.
últimos comentarios
Para culminar, los determinantes resultan ser útiles para resolver sistemas de ecuaciones lineales y de primer orden, y los métodos para lograrlo, se basa en un simple arreglo de filas y columnas con las técnicas y reglas mostrada anteriormente. La aplicación se puede reflejar en el calculo de áreas y volúmenes en espacio euclídeo, utilizando la notación de coordenadas aplicadas en esta área, así como la verificación de sistemas ortogonales y transformación de coordenadas, estos últimos conceptos de mayor explicación y complejidad.
Lo cierto es que se trata de un sistema que permite ordenar una gran cantidad de datos, en cual las operaciones simples de sumar, multiplicar y restar pueden aportar resultados importante y útiles. Sin mas que agregar permítanmen mostrar mi gratitud a los lectores de este post, esperando que sea de su agrado y gusto, como lo es para mi en la preparación de este contenido, así mismo deseo expresar que este trabajo es producto del interés que poseo por conocer los elementos básicos de la matemática, lo cual me lleva a investigar, aprender y compartir en esta respetada red, pues mi objetivo es conocer y desentrañar ( lo que permita mi capacidad cognitiva) los aspectos básicos, fundamentales y atractivo de la matemática, y exponerlo para desde mi perspectiva mostrar mi avance y aporte en la plataforma. Espero su apoyo y saludos a todos..!
Referencia bibliográfica con respecto al texto:
Todas las expresiones matematicas fueron realizadas en Power Point 2007
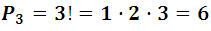
Muy buen post
Posted using Partiko Android
gracias @emiliomorles
He leído su post, profesor @juancmz. Este tema es un clásico y básico en álgebra lineal! Le sugiero especifique quién es el autor de todas las imágenes. No lo deje implícito. Saludos!
Ok muchas gracias @eniolw por tu sugerencia, ya corrijo ese detalle