Resumen.
Las primeras nociones de vector se comienzan a impartir a los estudiantes en el tercer año de educación media, sin embargo, la experiencia docente universitaria demuestra que el conocimiento de estos temas es impartido por los docentes de bachillerato de una manera incompleta y superficial, lo que conlleva una deficiencia muy fuerte en el estudiante, quien luego la manifestará al enfrentarse con cursos de niveles de estudios superiores, un ejemplo de esto se aprecia claramente en la materia Física 1, en ésta se enseña como primer tema el álgebra vectorial, y donde el profesor supone que el estudiante tiene los conocimientos previos del bachillerato, este tema es anterior a los temas relacionados con las leyes y principios de la mecánica de una partícula, donde el álgebra vectorial es de vital importancia.
En el departamento de Física de la Universidad del Zulia, Venezuela, la estadística indica que en la primera evaluación, que abarca el tema de vectores, el porcentaje de aplazados, tan sólo en el primer examen, es de alrededor del 75 %. Esta cifra alarmante sugiere que es necesario aplicar alguna estrategia de aprendizaje donde el estudiante pueda rápidamente captar y comprender la noción de vector y de los principios del álgebra vectorial. Para esto se diseñaron y construyeron una serie de objetos o modelos que representan entidades abstractas tales como los vectores y los sistemas coordenados. Se ideó una estrategia para usar estos objetos como recursos didácticos en la enseñanza del análisis vectorial.
Luego de la aplicación de estos recursos se evidenció un notable mejoramiento en el entendimiento del álgebra vectorial por parte de los estudiantes que cursaban la materia Física 1 en la Facultad Experimental de Ciencias, concretamente para las licenciaturas de Física, Química y Computación. Los resultados obtenidos arrojaron una disminución considerable en el número de aplazados en el primer tema a un porcentaje promedio del 45 %. Este resultado nos permite inferir que la utilización de estos recursos tuvo una fuerte influencia en el entendimiento y comprensión de los vectores y sus operaciones, así como de su representación espacial en los sistemas coordenados.
1. Introducción.
El análisis vectorial es una maquinaria matemática muy poderosa que permite reducir y simplificar el tratamiento de problemas en la física, sólo por medio de la matemática es posible presentar en forma fundamental y, hasta donde sabemos, precisa las leyes de la naturaleza. Sin embargo, comprender un sistema físico determinado en el sentido estrictamente matemático no es lo fundamental para entender el comportamiento real de dicho sistema, es decir, es necesario entender lo que realmente significan todos esos símbolos o términos matemáticos desde el punto de vista de la física, esto lo describió muy bien el físico premio nobel Paul A. M. Dirac cuando dijo: "Yo comprendo lo que significa una ecuación matemática si tengo el medio de representarme las características de las soluciones sin realmente resolver la ecuación". Así, si tenemos el medio de conocer que esta realmente sucediendo y que significa un determinado símbolo matemático en una circunstancia dada sin resolver efectivamente las ecuaciones, entonces habremos comprendido las ecuaciones, aplicadas a esa circunstancia particular. Lo que se quiere decir, en pocas palabras, es que la comprensión de la física no es algo completamente matemático, pero ésta es absolutamente necesaria.
La noción de vector es el principio de la comprensión del análisis vectorial y para esto se debe establecer su álgebra, ésta última junto con su representación espacial es el tema que nos interesa en este trabajo, se pretende crear una experiencia vivencial entre el estudiante del primer curso de física y el álgebra vectorial mediante la explicación del tema por parte del profesor usando modelos físicos construidos artesanalmente, estos modelos representarán las entidades abstracto-matemáticas entre las que resaltan los vectores, los sistemas coordenados, los ejes cartesianos, el espacio euclídeo, líneas y escalas entre otras.
Esta experiencia directa tiene la capacidad de estimular una implicación más personal, y con ello encaminar a los alumnos a una mejor comprensión de lo que significa físicamente un vector y como puede operar con él siguiendo lo establecido por el álgebra vectorial. Cada modelo se ha diseñado con las representaciones seguidas por las clases tradicionales y los textos de física de todos los autores, es decir, se ha seguido toda la convención universal del
metalenguaje de la física y la matemática sin cambiarse ninguna forma o representación de los símbolos físico-matemáticos. Al contar con modelos reales, el estudiante podrá palpar y experimentar cada ente matemático como si fuera un objeto real, esto involucra la experiencia de los sentidos de la visión y del tacto, cosa que no sucede con la exposición tradicional del profesor quien los hace a partir de dibujos y escritura en el pizarrón o en proyecciones digitales de los símbolos y entidades fisico-matemáticas. Mediante esta estrategia el estudiante podrá observar toda la explicación de una manera directa y completa desde el punto de vista espacial, es decir, los modelos u objetos tales como los vectores y sistemas coordenados son ahora objetos reales y por lo tanto en tres dimensiones.
Es importante resaltar, que esta estrategia no pretende en ninguna circunstancia sustituir el uso del pizarrón o de proyecciones para desarrollar las clases, muy por el contrario, se incluyen en dicha estrategia, esta solo pretende ser usada como complemento a la enseñanza tradicional, la idea principal es que el estudiante se estimule y motive por el entendimiento de las matemáticas y su implicación dentro de la física, su significado y su aplicación en el mundo real.
2. Metodología.
2.1. Descripción del contexto.
El curso de Física 1 forma parte de las materias contenidas en el plan de formación de todas las licenciaturas de la Facultad Experimental de Ciencias de la Universidad del Zulia: Física, Química, Biología y Computación; a pesar de que los programas pueden variar de una licenciatura a otra, incluso el número de horas de clase y las prácticas de laboratorio, el tema de vectores y álgebra vectorial no puede por ningún motivo quedar fuera del programa. Todas las licenciaturas deben comprender lo que es un vector y su álgebra ya que ésta es una cantidad física fundamental que representa cantidades tales como: desplazamiento, velocidad, aceleración, fuerza, campos eléctricos y magnéticos, torque, mementum lineal, momentum angular y otras cantidades que siempre identificarán el comportamiento de un sistema natural o artificial, esto puede comprender entre otros, un microprocesador, una celda solar, el clima en una zona determinada, una planta, una bacteria, un automóvil, y muchísimos más.
La ciencia real jamás podrá, hasta donde sabemos, desprenderse o ignorar estas cantidades físicas ya que ellas son las que componen todos los sistemas del universo. Generalmente la evaluación de la comprensión de este tema se realiza mediante la realización de tareas individuales, talleres grupales y un examen individual escrito. Las ponderaciones de los valores de la nota puede variar según la apreciación de cada profesor, pero por excelencia se toma el examen escrito como el de mayor peso. El estudiante debe haber acumulado un total de créditos suficientes que debe ser mayor o igual a diez puntos para aprobar la asignatura.
2.2. Diseño y construcción de los recursos didácticos.
Los recursos didácticos son una serie de modelos u objetos construidos artesanalmente con materiales resistentes, principalmente cabillas finas de acero, esto se hizo con la intención que fuesen perdurables y resistentes al desgaste debido a la utilización constante por parte de los estudiantes. Cada uno se pintó con colores vivos que llamaran la atención y se establecieron una serie de colores que representaban alguna entidad matemática, como por ejemplo, en los ejes cartesianos el verde para el eje "x", el azul para el eje "y", y el rojo para el eje "z"; de igual manera para los diferentes octantes del espacio euclídeo se pintó un color diferente. A continuación se explica cada diseño de construcción y su significado desde el punto de vista físico-matemático.
2.2. 1. El vector.
Un vector es una cantidad físco-matemática que posee tres propiedades fundamentales: magnitud, dirección y sentido; estas propiedades son las que definen un vector. En la mayoría de los textos de física la notación de vector es una letra mayúscula en negrita y la magnitud del vector se simboliza por medio de esa letra en negritas pero encerrada entre barras, o simplemente la letra pero no en negrita (letra normal); el profesor representa el vector en el pizarrón
en manuscrito por medio de la letra mayúscula con una flecha o semiflecha arriba, y su magnitud de la misma manera, pero encerrada entre barras o simplemente la letra mayúscula sin flechas, es decir:
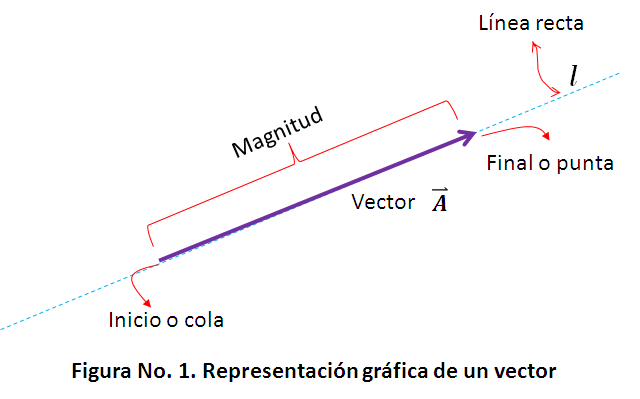
Para visualizar el vector desde el punto de vista geométrico o gráfico se usa una flecha, esta flecha posee un inicio o cola y un final o punta, la magnitud del vector vendrá dada por la longitud de la flecha, es decir, la distancia de la cola a la punta; la flecha está contenida en una línea recta l, esta recta indica la dirección del vector y la punta de la flecha indicará su sentido ver Fig. 1.
La construcción del vector consistió en una flecha de acero, donde se pintó la punta y la cola de diferentes colores para resaltar su significado, ver Fig. 2.
2.2. 2. El espacio euclídeo.
Para representar el espacio euclídeo se construyó en madera una especie de caja cúbica abierta en la que se muestran los ocho octantes del espacio tridimensional, cada octante se pintó de un color diferente y se tomaba el octante positivo, es decir, con los ejes "x", "y" y "z" positivos, arbitrariamente. Este diseño ayudó enormemente al estudiante a identificar los planos en el espacio, es decir los planos x = 0, y = 0 y z = 0, del sistema de coordenadas cartesiano, ver Fig. 3.
2.2. 3. Los ejes coordenados.
Los tres ejes coordenados cartesianos se construyeron con cabillas de acero, cada cabilla representa un eje coordenado los cuales se pintaron de diferentes colores, verde el eje x, azul el eje y y rojo el eje z, los tres ejes se cruzaron en un punto en común el cual se unió mediante soldadura, cada eje tiene su lado positivo y negativo, al final de cada eje se colocó una flecha que indica su dirección y se pintó de color blanco, ver Fig. 4. Este modelo de los ejes coordenados junto con el del espacio euclídeo ayudó enormemente al estudiante a poder ubicar los vectores en el espacio, así como la ubicación de puntos y coordenadas en tres dimensiones.
2.2. 4. Un vector en el espacio.
Con la intención de explicar la representación de un vector en el espacio y sus respectivas componentes, es decir, poder apreciar en tres dimensiones el vector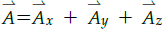 
se construyó un vector ubicado en el espacio tridimensional, ver Fig. 5. Esta representación ayudo al profesor en la explicación de elementos matemáticos tales como, los vectores unitarios bases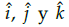 
y los vectores unitarios en una dirección cualquiera 
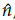, esto obviamente simplificó mucho el tratamiento explicativo es estas entidades matemáticas.
2.2. 5. Suma y resta de vectores.
Para la suma y resta de vectores se construyeron modelos que representaban dichas operaciones utilizando el método del paralelogramo y del polígono, ver Fig. 6 y 7. Esto con ayuda de la explicación en el pizarrón ayudó al estudiante a poder “ver” y “palpar” en tres dimensiones estas operaciones así como los métodos gráficos que tradicionalmente sólo se ven en el pizarrón o en proyecciones digitales.
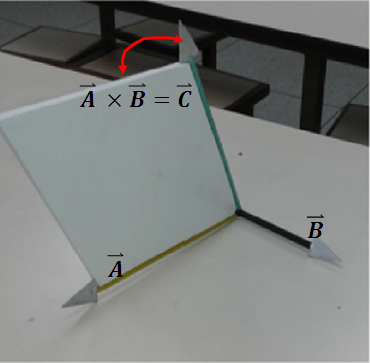
2.2. 5. Producto vectorial.
El el álgebra vectorial una de las cosas que más le cuesta al estudiante entender bien es el producto vectorial desde el punto de vista gráfico, generalmente, para determinar la dirección del resultado de un producto vectorial, es decir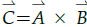 
, se aplica una técnica llamada: técnica de la mano derecha, el profesor debe explicar esto haciendo coincidir los dos vectores 
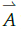y 
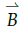en su origen, luego toma con la palma de la mano el primer vector, es decir, 
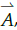, luego cierra su puño en dirección al vector 
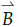pero extiende su dedo pulgar, a donde apunta este dedo es la direccón del vector resultante del producto vectorial, es decir, el vector 
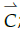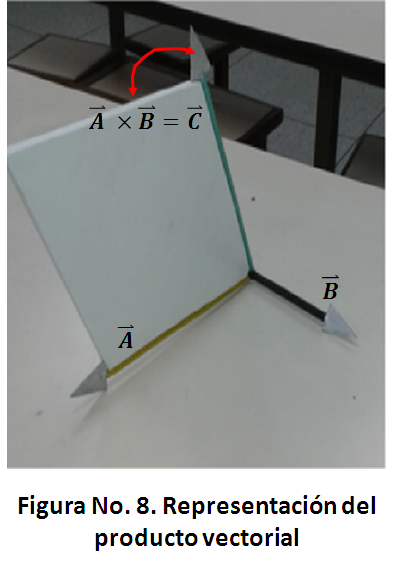
; el producto vectorial es una operación que necesariamente se debe explicar en tres dimensiones, pero la explicación del profesor es prácticamente en dos dimensiones, ya que lo hace con los vectores dibujados en el pizarrón, queda en la creatividad del profesor extrapolar su explicación de alguna manera de dos a tres dimensiones. Para evitar esto, la construcción del modelo del producto vectorial se hizo por medio de dos vectores de diferentes colores con un ángulo determinado entre ellos y con una porción del plano -hecho en madera y pintado de blanco-, que contiene a esos dos vectores, el resultado del producto vectorial de estos vectores, ya sean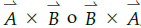 
, son dos vectores perpendiculares al plano y se colocaron en sentidos opuestos coincidiendo en su origen para poder explicar la no conmutatividad de este importante producto vectorial, ver Fig. 8. La explicación se hacia mucho más sencilla y el estudiante podía ver fácilmente la dirección del producto vectorial de 
.
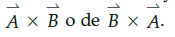Conclusiones.
El uso de los modelos reales construidos y diseñados con el propósito de servir como nuevos recursos didacticos para la enseñanza del álgebra vectorial han dado resultados satisfactorios, se evidencia un mejor entendimiento de la noción de vectores, del espacio tridimensional y de los sistemas coordenados. El estudiante se motiva al ver posible que puede “palpar” y “ver” mejor las identidades abstractas de la físico-matemática. El rendimiento de los estudiantes en los talleres grupales y exámenes individuales mejoró notablemente.
El diseño y construcción de estos recursos se puede extender mucho más a otras áreas del álgebra y del análisis vectorial, se puede incluso abarcar otros temas que puedan ayudar al estudiante al mejor entendimiento de la física. Como se mencionó anteriormente estos recursos didácticos y estrategias de enseñanza son una alternativa que puede complementar la enseñanza tradicional de estos temas tan abstractos y muchas veces difíciles para el estudiante que generalmente trae una base muy débil del bachillerato.
Referencias.
[1] Feynman R. P., Leighton R., Sand M. Física. Mecánica, radiación y calor, Addison-Wesley Iberoamericana, Wilmington, Delaware, USA, 1987.
[2] VerLee L., Aprender con todo el cerebro, Martínez Roca, Colombia, 1997.
[3] Kittel Ch., Knight W., Ruderman M., Mecánica, Serie Berkeley, Vol. 1, Reverté, Barcelona, 1989.
[4] Young H. Freedman R., Física Universitaria, 12da. ed., Addison-Wesley, México, 2009.
Me gusta mucho tu idea, personalmente creo que todos los profesores deberían hacer manejo de estos recursos para "motivar" un poco más a los estudiantes ya que es un tema aveces un poco tedioso para algunos y esto tal vez los ayude a comprender más rápido los conceptos.
You're so nice for commenting on this post. For that, I gave you a vote!
Muchas gracias por tu comentario. De verdad agradezco esto ya que me motiva a seguir haciendo este tipo de trabajos para mejorar la educación de las ciencias físicas y matemáticas.
Felicidades!
excelente, una manera muy clara y precisa de comprender, saludos.
Muchas gracias. Este es un impulso muy fuerte para seguir trabajando en este campo donde podré mejorar la forma de la enseñanza de la física de una manera diferente y dinámica entre los profesores y el estudiante.
Muchas Gracias. El que valoren mi trabajo me llena de entusiasmo para seguir trabajando en estos diseños y metodologías de nuevas formas de enseñar la física y la matemática.
Muchas gracias.
Excelente trabajo, me da gusto leer publicaciones con este tipo de contenido de muy buena calidad.
Interesante!
Muchas Gracias amiga.
Muy interesante tu artículo.
Hay tantas formas de aprender como los tipos de inteligencia existentes. Ese modelo sería muy adecuado para una inteligencia kinestésica.
Muchas gracias. Me parece interesante eso de la kinestésica. Me gustaría discutirlo para aprender al respecto, ya que no se nada de ese tema. Gracias
Soy preparador de física y matemática de la USB Caracas. Buen artículo para aquellos estudiantes con dificultades. Te seguiré leyendo. Saludos.
Muy didáctica tu publicación, saludos
Hermano felicitaciones por tu post. Estrategias didácticas como las que planteas realmente deben facilitar el aprendizaje de la noción de vector y el producto vectorial de vectores, a la vez que motivarían a los estudiantes durante el proceso, pues pueden palpar y "sentir" las tan útiles "flechas" en el campo de la Física. Te felicito por tu aporte. ¡Saludos y un abrazo!
Excelente explicación, me encanta tu post
@rnunez09 excelente trabajo, me parece muy didáctica tu estrategia. Sigue divulgando trabajo de calidad.