Comunidad @stem-espanol y comunidad de Hive en general, vayan mis cordiales saludos para todos. Mis amigos Hive-Lectores, como ya he estado diciendo en mis posts anteriores, además de hacer llegar un poco de ciencia a la comunidad de Hive en general espero, con el presente contenido, seguir contribuyendo con la formación de aquellos estudiantes que por el COVID-19 deben seguir sus estudios en casa.
El presente post es la segunda parte de mi anterior post:
MOVIMIENTO ARMONICO SIMPLE, UNA PRESENTACION DIDACTICA - Parte 1
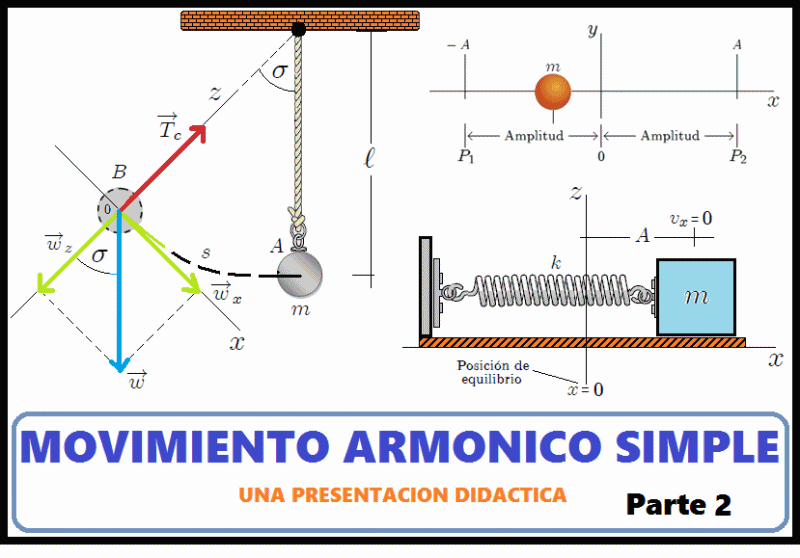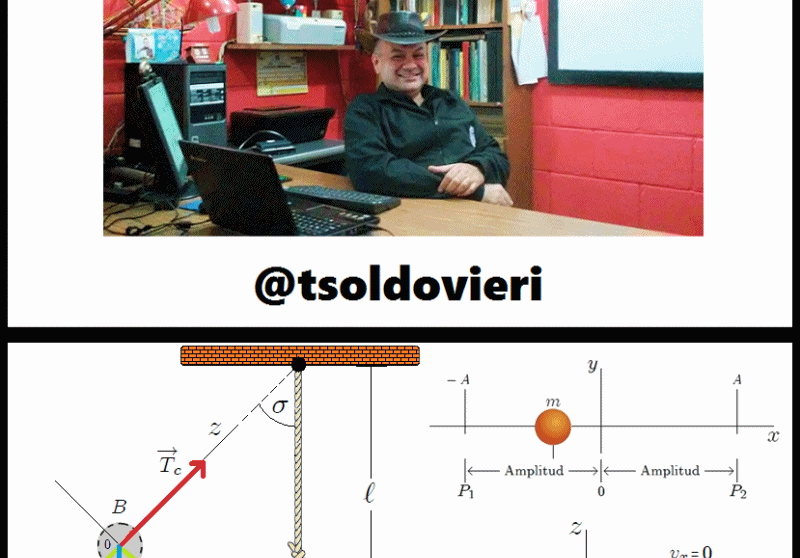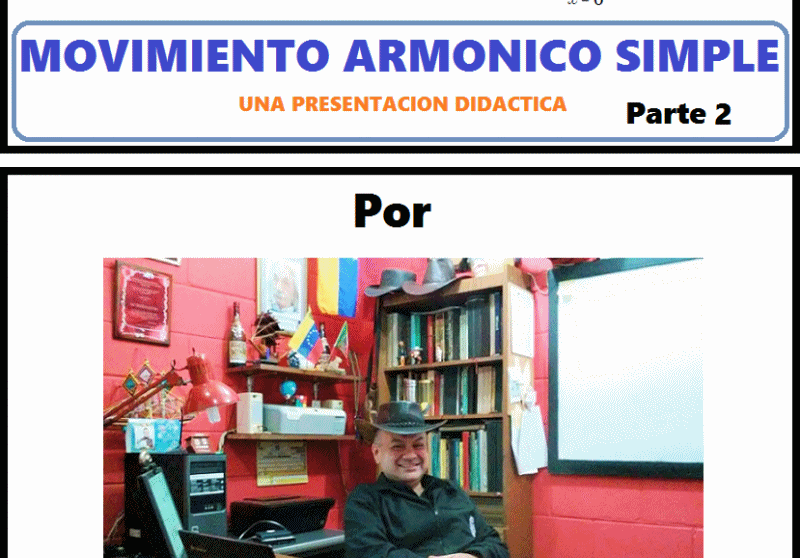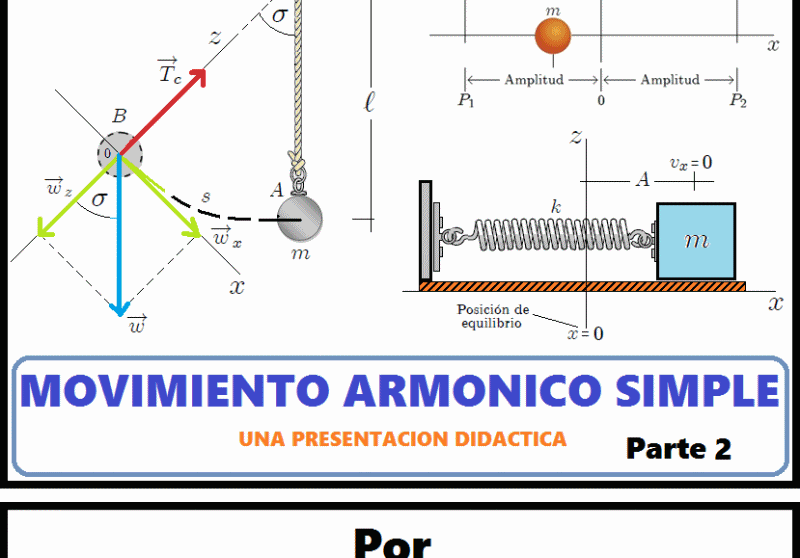
Mis estimados Hive-Lectores, continuando con mi anterior post, ahora les hablaré acerca de la energía en el Movimiento Armónico Simple (MAS) y la relación que tiene este último con el Movimiento Circular Uniforme (MCU).
Como les mostré en mi anterior post, la posición de una partícula cuya ecuación de movimiento sea,
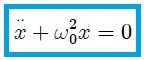
viene dada por las siguientes dos soluciones a la misma,
donde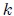 
es una constante positiva y 
.
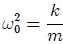Usaremos, mis estimados Hive-Lectores, la primera de las soluciones (2) de aquí en adelante (usar la segunda es equivalente).
Ahora bien, procederemos primeramente a encontrar la Energía Cinética de la partícula. Como se sabe, la energía cinética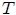 
para una partícula que se mueve a lo largo del eje 
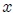(como es nuestro caso) es dada por,
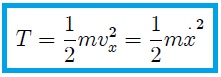
donde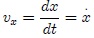 
es la rapidez de la partícula en el antes mencionado eje. Al introducir la primera de las soluciones (2) en la anterior expresión obtenemos, después de unos muy simples cálculos,
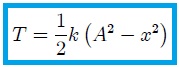
que es la energía cinética del cuerpo en función de su posición .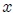
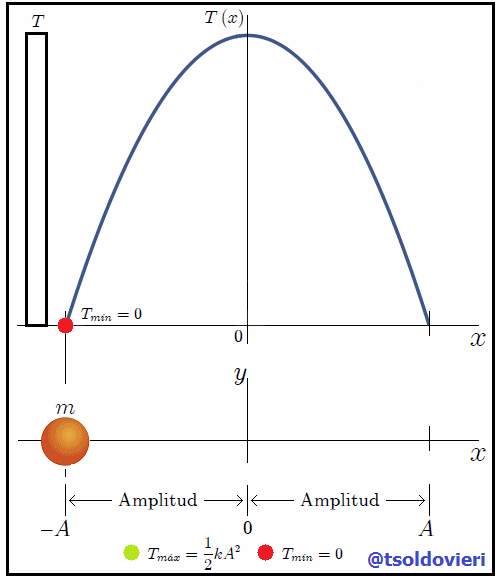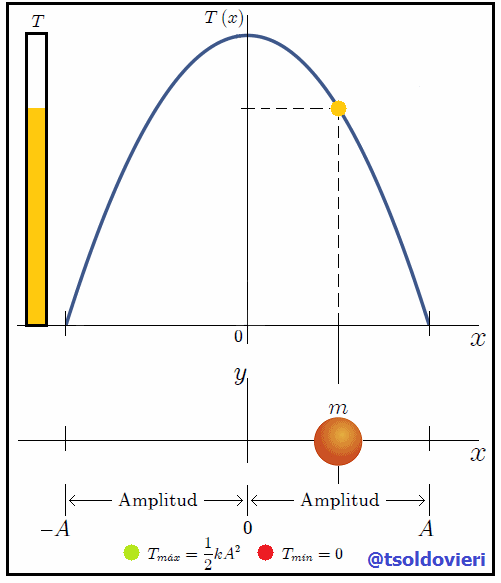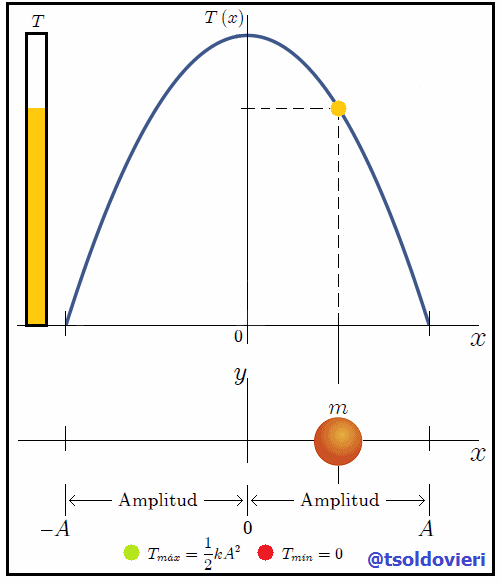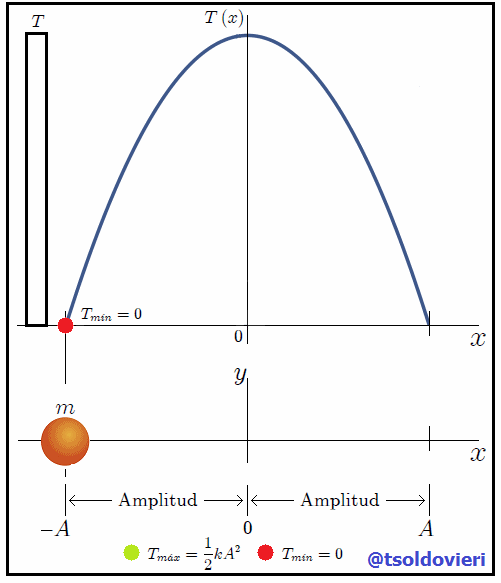
Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint y PhotoScape
En la figura 1 les muestro una gráfica de la expresión (4). Observemos, mis amigos Hive-Lectores, como la energía cinética es nula en los extremos de la trayectoria, es decir, en las posiciones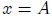 
y 
y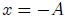a que en las mismas la rapidez del cuerpo es nula, en perfecta concordancia con dicha expresión. A las posiciones donde la energía cinética es nula, que es la energía cinética mínima 
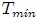del cuerpo, se les denomina Puntos de retorno. En la posición 
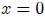podemos observar que la energía cinética toma su valor máximo 
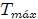de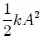 
.
La Energía Potencial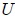 
, por otro lado, viene dada por el trabajo realizado para desplazar al cuerpo desde la posición 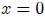hasta una posición 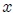en contra de la fuerza 
,
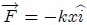donde he usado ~ para distinguir entre la variable y el límite de integración. Por lo tanto, al sustituir la fuerza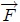 
en la anterior expresión resulta,
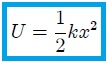
siendo esta expresión la energía potencial del cuerpo en función de su posición .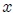
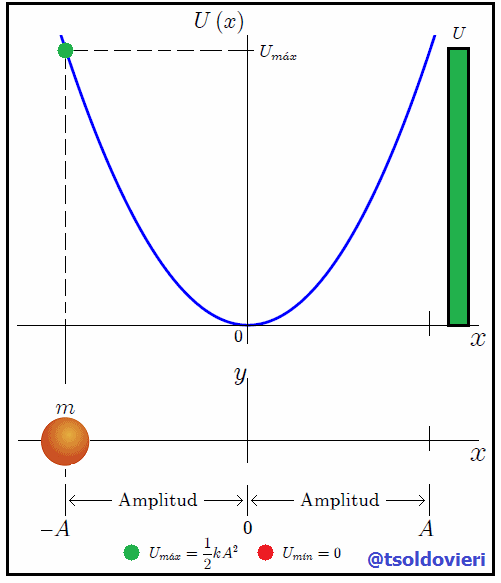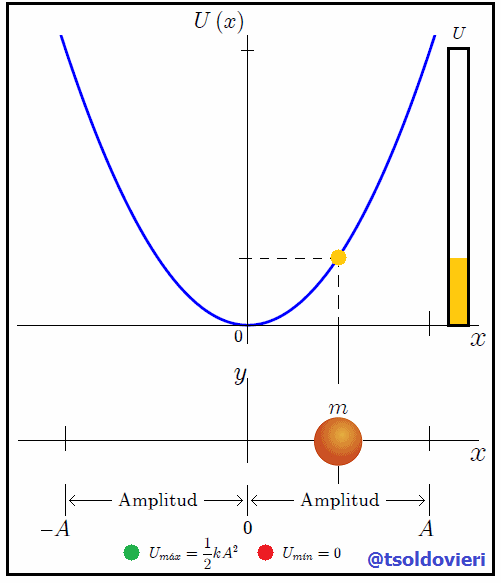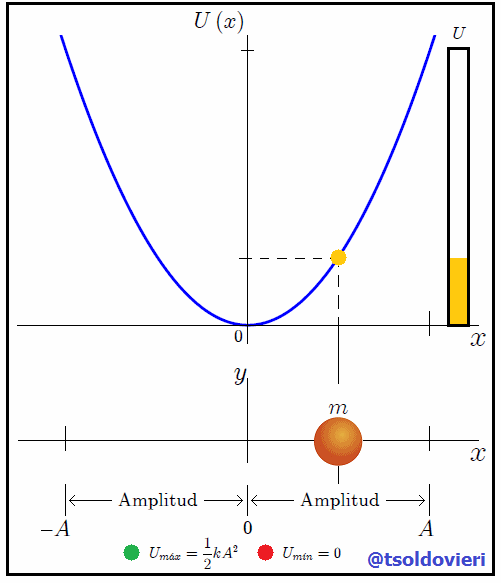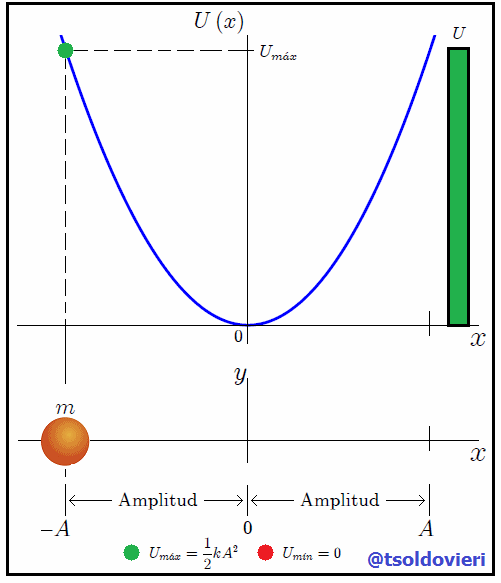
Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint y PhotoScape
Mis estimados amigos Hive-Lectores, en la figura 2 les muestro una gráfica de la expresión (6). Observemos ahora como la energía potencial es nula, su valor mínimo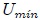 
, donde antes la energía cinética tomaba su valor máximo 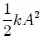, es decir, en la posición 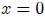. En las posiciones 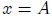y 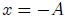, donde la energía cinética es mínima, la energía potencial toma su valor máximo 
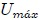de .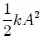
Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint y PhotoScape
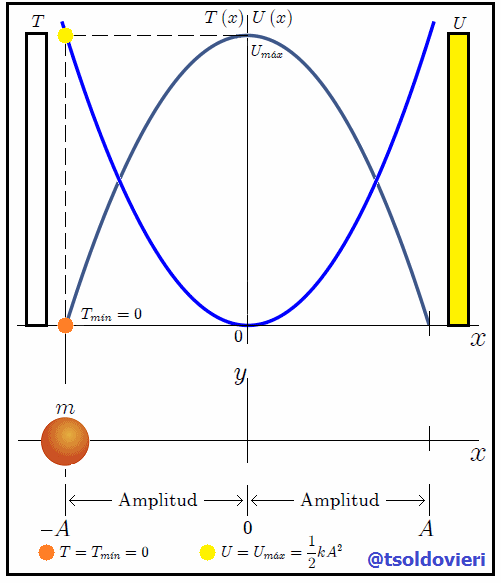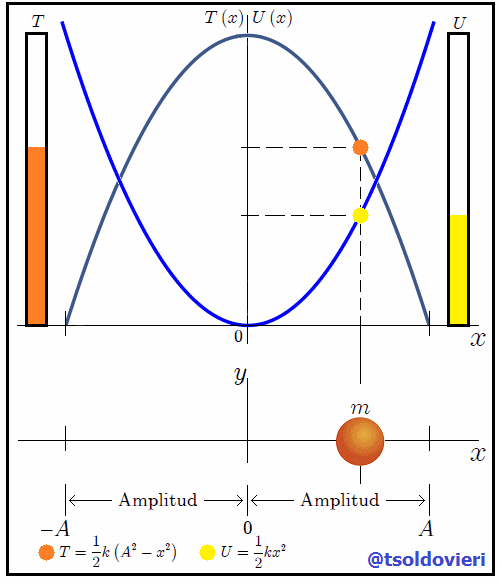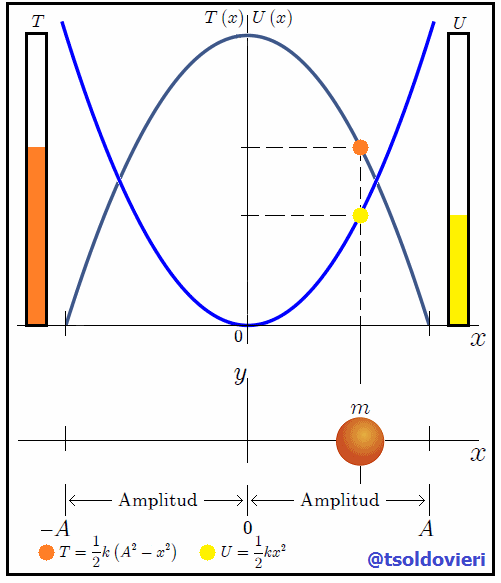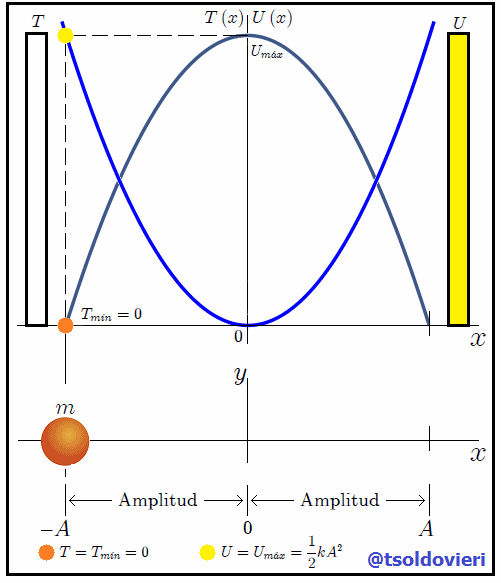
En la figura 3, mis estimados amigos Hive-Lectores, les muestro la energía cinética y la energía potencial en una misma gráfica, en la cual podemos observar que hay dos posiciones donde la energía potencial se hace igual a la energía cinética. Estas posiciones son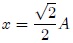 
y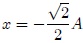 
, las cuales son trivialmente obtenidas al igualar (4) y (6), siendo los puntos donde se entrecruzan las gráficas de ambas energías.
En todo lo anterior ocurre algo muy notorio. El valor máximo de las energías cinética y potencial es 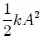, manteniéndose así en el transcurso del tiempo. Es decir, el sistema no puede tener una energía mayor a la anterior. La anterior cantidad representa la Energía Mecánica Total 
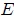del sistema, la cual se conserva (permanece constante) por lo que se dice que el sistema es conservativo. Lo anterior era de esperarse ya que en el sistema no existen fuerzas disipativas (fuerzas de fricción) que den lugar a pérdida de energía. La energía mecánica total viene dada por la suma de la energía cinética y la energía potencial y, para este caso, es fácil encontrar que,
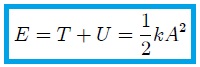
Para finalizar les mostraré, mis estimados amigos Hive-Lectores, la relación existente entre el MAS y el MCU. Algunos dispositivos comunes en la vida cotidiana muestran una correspondencia entre movimiento oscilatorio y movimiento circular. Por ejemplo, el pistón en el motor de un automóvil (vean la figura 4) sube y baja (movimiento oscilatorio) aunque el resultado de este movimiento es el movimiento circular del cigüeñal.
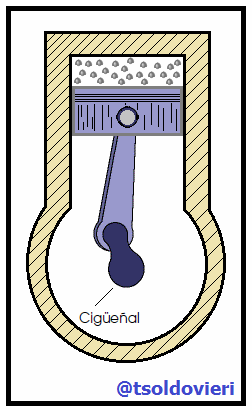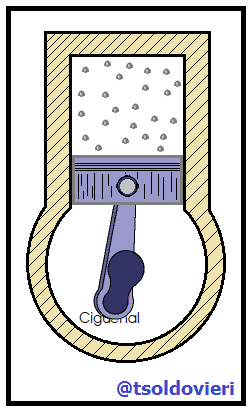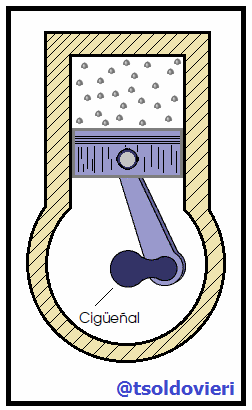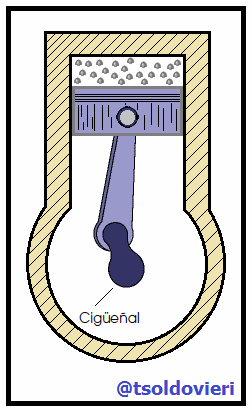
Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint y PhotoScape
En un motor a vapor como en el de los trenes antiguos (vean la figura 5), el eje impulsor va de atrás para adelante en movimiento oscilatorio, lo que provoca un movimiento circular de las ruedas.
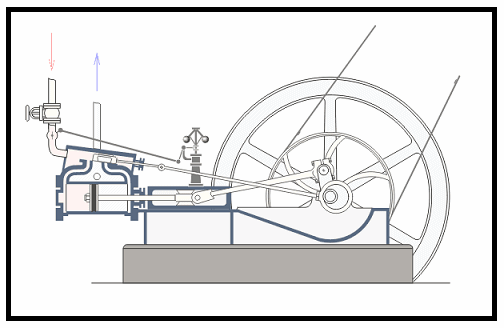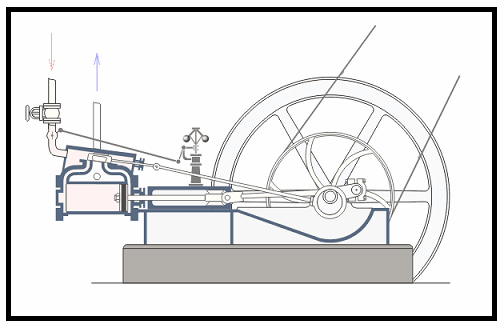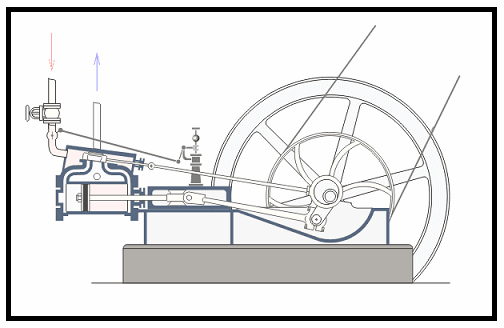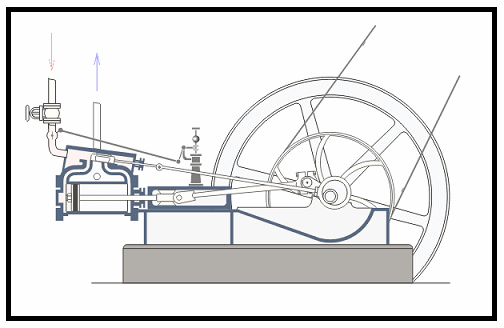
By Panther - Steam engine in action.gif - CC BY-SA 3.0 - Fuente
Para explorar la relación existente entre el MAS y el MCU, consideremos una partícula ubicada en el punto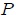 
sobre la circunferencia de un círculo de radio 
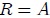, como les muestro en la figura 6(a) , con la línea 
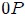que forma un ángulo 
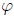con el eje 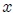en el tiempo 
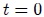. Llamemos a este círculo círculo de referencia para comparar el MAS con el MCU, y elijamos la posició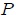n en 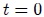como la posición de referencia.
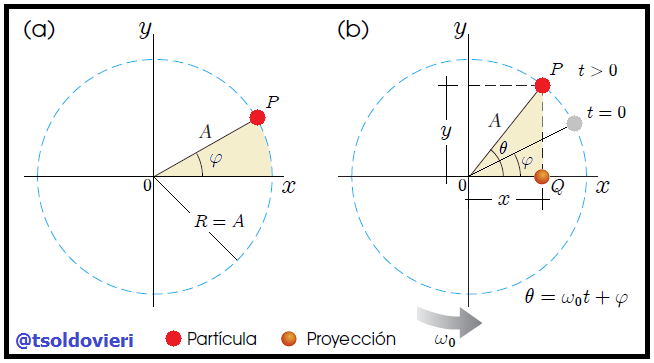
Imagen realizada por mi persona, @tsoldovieri, usando la aplicación Paint
Si la partícula se mueve a lo largo de la circunferencia con rapidez angular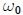 
constante hasta que 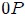forma un ángulo 
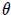con el eje 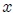, como les muestro en la figura 6(b)b, en algún tiempo 
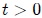el ángulo entre 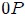y el eje 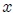es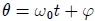 
. Conforme la partícula se mueve a lo largo de la circunferencia, la proyección de 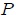sobre el eje 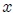, el punto 
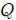, se mueve de atrás para adelante a lo largo del eje 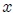entre los límites 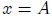y 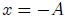, como les muestro en la figura 7.
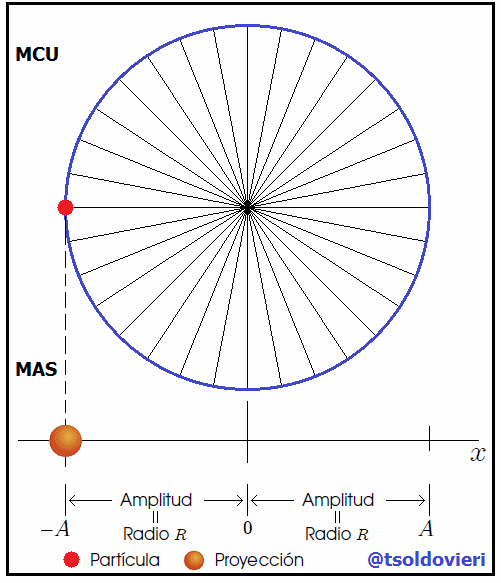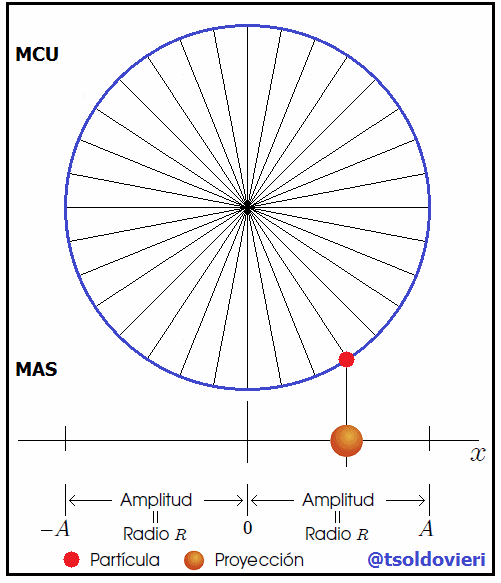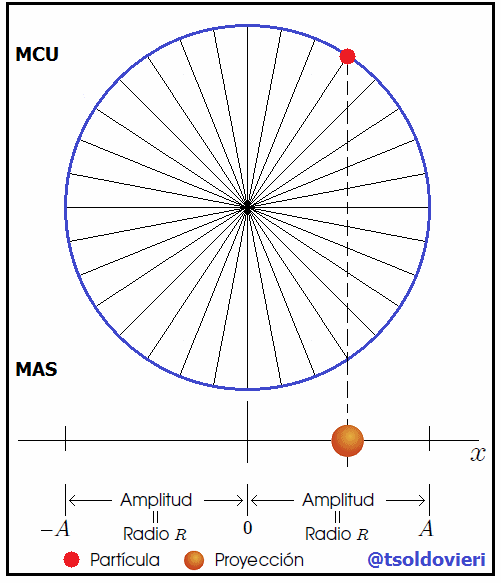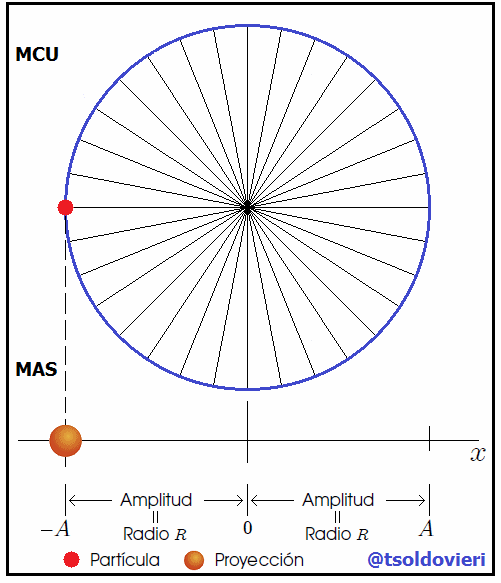
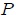y su proyección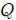 Gif animado realizado por mi persona, @tsoldovieri, usando las aplicaciones Paint y PhotoScape
Notemos que los puntos 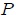y 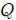siempre tienen la misma coordenada 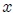, siendo muy fácil determinar a partir del triángulo rectángulo 
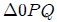que esta coordenada viene dada por,
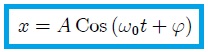
La anterior expresión es la misma que la ecuación (2) que obtuvimos para el MAS y muestra que el punto 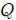se mueve con MAS a lo largo del eje 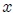. Por lo tanto, el MAS a lo largo de una línea recta se puede representar mediante la proyección del MCU a lo largo de un diámetro de un círculo de referencia.
En vista de lo antes discutido, podemos decir que la cantidad 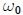introducida en la primera parte de este post, se interpreta físicamente como una frecuencia angular y 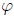es un ángulo inicial de comienzo del movimiento.
BIBLIOGRAFIA RECOMENDADA
Aquí les presento algunos textos que recomiendo si desean ahondar en el tema:
Soldovieri C., T. FISICA GENERAL - UNA INTRODUCCION A LOS FLUIDOS, VIBRACIONES Y TERMODINAMICA. Preprint, 2020. El borrador se puede descargar desde mi web personal: http://www.tsoldovieritsweb.ihostfull.com
Bauer, W. & Westfall, G. D. FISICA PARA INGENIERIA Y CIENCIAS, volume 1. McGraw-Hill/Interamericana de México, S. A. de C. V., 2011.
Bueche, F. J. & Hecht, E. FISICA GENERAL. Schaum. McGraW-Hill / Interamericana Editores, S.A. de C.V., México, 10ma edition, 2007.
Fishbane, P. M.; Gasiorowicz, S. G. & Thornton, S. T. PHYSICS FOR SCIENTISTS AND ENGINEERS WITH MODERN PHYSICS. Pearson Education Inc., 3th edition, 2005.
Burbano de E., S.; Burbano G., E. & Gracia M., C. FISICA GENERAL. Editorial Tébar, S.L., 2003.
Halliday, D.; Resnick, R. & Krane, K. S. FISICA, volume 2. Compañía Editorial Continental, S.A. de C.V., México, 4ta edition, 1994.
Hewitt, P. G. CONCEPTOS DE FISICA. Editorial Limusa, México, 1era edition, 1992.
Estimados amigos Hive-Lectores. Espero que la anterior información les sea de mucha utilidad. Si tienen preguntas, no duden en hacérmelas llegar pues, con mucho gusto, les atenderé. Igualmente, si tienen detalles que puedan nutrir o mejorar la anterior información, por favor, háganmelas saber. Hasta la siguiente parte del presente post ¡Saludos a todos! 😁.
LES INVITO VISITAR MI WEB PERSONAL www.tsoldovieritsweb.ihostfull.com
En esta página web podrás conseguir los borradores de los libros de texto que estoy escribiendo y varias listas de problemas con respuestas de: Optica, Mecánica Clásica, Mecánica Cuántica, Física General 1, Física General 2 y Física General 3. También encontrarás enlaces a otras páginas web de interés.
Deja tus comentarios en el libro de visitas! 😁
Mis amigos Hive-Lectores,
PARA APRENDER A PENSAR COMO FISICO HAY QUE RESOLVER MUCHISIMOS PROBLEMAS Y LLORAR LAGRIMAS DE SANGRE (ASI ES LA VIDA, LA VIDA ES CRUEL!) PUES LA PRACTICA ES FUNDAMENTAL, ES DECIR, HAY QUE HACER DE NUESTROS CEREBROS UNOS FISICO-CULTURISTAS. HAY QUE HACERLES SALIR MUSCULOS!!!. Terenzio Soldovieri C. |
|---|
Muy bien abordado el tema profesor. Saludos y gracias por compartir. Saludos.
Muchas gracias por el apoyo @hispapro y amigo @carlos84. Gracias por considerar mi trabajo. Mis cordiales saludos.
Congratulations @tsoldovieri! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board And compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Thanks for the support @hivebuzz.
You are very welcome @tsoldovieri 👍🙂
Saludos querido profesor @tsoldovieri. Impecable clase de Mecánica Clásica. Épico su mensaje motivacional para aprender a ser Físico.
Muchas gracias por pasar y comentar mi post amigo @djredimi2. Muy épico 😁.
Con miras a enseñar, esta entrada reviste arte y destreza. Excelente @tsoldovieri.
Gracias @capp por tomar parte de tu tiempo en pasar y comentar mi post. Gracias por tu motivador comentario. Mis cordiales saludos.
Excelente abordaje sobre la energía del movimiento armónico simple, útil para el entendimiento del movimiento de sistemas mecánicos. Ideal para estudiantes de ingeniería. Saludos!
Gracias amigo @acont. Esa es la idea, que sea en verdad útil para los estudiantes en esta época tan difícil. Mis cordiales saludos.
Congratulations @tsoldovieri!
You raised your level and are now a Minnow!
Do not miss the last post from @hivebuzz: