Las Ecuaciones Fundamentales de la Hidrostática, como su nombre lo indica, son el punto de partida para el completo estudio de la rama de la Mecánica de Fluidos denominada Hidrostática. Esta última es la dedicada al estudio de los fluidos en reposo y, por esta razón, también se le denomina Estática de Fluidos. El Teorema de Pascal es una de sus consecuencias, el cual tiene innumerables aplicaciones en la ciencia y en la industria. En lo siguiente, les presentaré cómo se puede llegar a las Ecuaciones Fundamentales de la Hidrostática y al mencionado teorema a partir de las mismas. Intentaré hacerlo de la forma más clara y sencilla posible, dentro de lo que me permita hacer este tema tan técnico.
ES PERTINENTE, EN ESTE MOMENTO, HACER NOTAR QUE LAS IMAGENES AQUI PRESENTADAS, EXCEPTO AQUELLAS A LAS QUE SE LES INDICA LA FUENTE, FUERON COMPLETAMENTE ELABORADAS POR MI UTILIZANDO LA APLICACION PAINT INCLUIDA EN EL SISTEMA OPERATIVO WINDOWS 10, LAS CUALES FORMAN PARTE DE MI TEXTO TITULADO: FISICA GENERAL - Una introducción a los Fluidos, Vibraciones y Termodinámica. ESTE ULTIMO ESTAN INDICADO EN LA BIBLIOGRAFIA AL FINAL DEL PRESENTE POST. 😁
CONOCIMIENTOS BASICOS
Para abordar el estudio de las ecuaciones fundamentales de la Hidrostática y el Teorema de Pasca como una de sus consecuencias, es necesario antes tener presente los siguientes conocimientos básicos:
FLUIDO
Se denomina Fluido a toda aquella sustancia que cede inmediatamente a cualquier fuerza tendiente a alterar su forma, con lo que fluye y se adapta a la forma del recipiente. Los fluidos pueden ser líquidos o gases. |
|---|
Las partículas que componen un líquido no están rígidamente adheridas entre sí, pero están más unidas que las de un gas. El volumen de un líquido contenido en un recipiente hermético permanece constante y el líquido tiene una superficie límite definida. En contraste, un gas no tiene límite natural, se expande y difunde en el aire disminuyendo su densidad. A veces resulta difícil distinguir entre sólidos y fluidos debido a que los sólidos pueden fluir muy lentamente cuando están sometidos a presión como, por ejemplo, ocurre en los glaciares.
ACCIONES MECANICAS SOBRE LOS FLUIDOS
Para estudiar la Hidrostática es conveniente dividir las fuerzas actuantes sobre un elemento de volumen en dos categorías principales:
Fuerzas de superficie
Son las fuerzas que ejercen los elementos en contacto con el elemento de volumen 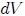 , como otros elementos de fluido, paredes, cuerpos en contacto, etc. |
|---|
Lo anterior es en el sentido de que el volumen considerado puede pensarse estar encerrado en una especie de película de contorno que lo mantiene separado de todo aquello que le circunda. Será denotada como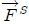 
.
Fuerzas de volumen
Son aquellas acciones ejercidas por elementos capaces de ejercer fuerzas proporcionales al volumen dV del elemento considerado. |
|---|
Por ejemplo: la fuerza gravitacional o la fuerza centrífuga, que siendo proporcionales a la masa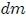 
contenida en el elemento de volumen 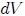, resultan proporcionales al mismo volumen por efecto de la relaci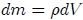ón 
, con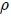 
uniforme dentro de 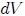. Será denotada como 
.
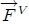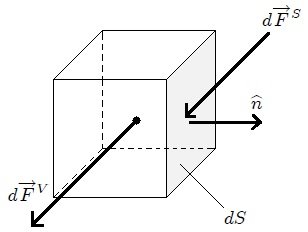
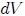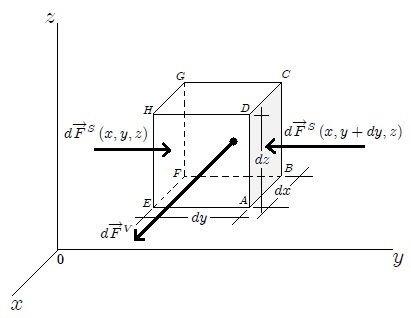
.Al considerar un elemento de volumen 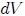, como el mostrado en la figura 1, donde una de sus caras tiene un área 
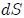cuyo vector normal es 
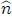, la fuerza de superficie que del exterior se ejerce sobre 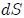está representada por 
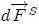. La fuerza de volumen saliente del elemento de volumen 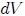es indicada con 
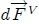y puede ser expresada mediante la relación,
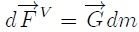
que evidencia la proporcionalidad directa a la masa, donde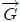 
representa un vector que tiene las dimensiones de una aceleración. Por ejemplo, en el caso de que la fuerza de volumen sea sólo el peso, se tiene que 
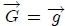, donde 
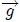es la aceleración debida a la gravedad.
Es de utilidad descomponer 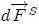en una componente 
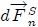normal a 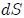y una componente 
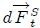tangencial a 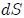. A estas componentes se les denominan Esfuerzos y se definen como,
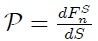
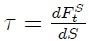
Nótese que los esfuerzos, que son cantidades escalares, poseen las dimensiones de una fuerza por unidad de superficie.
LA PRESION
Existe una diferencia en la manera en que una fuerza superficial 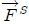actúa sobre un fluido y sobre un sólido. En un sólido no existe ninguna restricción respecto a la dirección de tal fuerza. En un fluido en reposo, la fuerza superficial debe estar siempre dirigida perpendicularmente a la superficie de dicho fluido (ver figura 2).
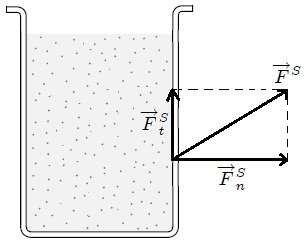
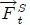de la fuerza de superficie 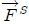en un fluido en reposo debe ser nula porque, de lo contrario, dicha componente haría que el fluido fluyera.Un fluido en reposo no puede soportar una fuerza tangencial 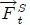ya que, en ese caso, las diferentes capas de fluido simplemente resbalarían unas sobre las otras, de hecho, es esta habilidad de los fluidos para resistir dichas fuerzas tangenciales lo que les permite cambiar su forma o fluir. Por lo tanto, para un fluido sin movimiento el esfuerzo de corte es nulo, mientras que el esfuerzo normal no lo es. A este esfuerzo normal se le da el nombre de Presión y puede escribirse simplemente como,
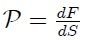
donde se ha supuesto de antemano que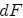 
es el elemento de fuerza normal aplicado sobre el elemento de superficie 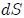. Entonces,
La Presión 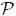 es la fuerza por unidad de superficie que ejerce un líquido o un gas perpendicularmente sobre una superficie determinada. |
|---|
donde se ha supuesto de antemano que 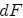es el elemento de fuerza normal aplicado sobre el elemento de superficie 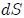. Entonces,
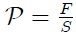
ECUACIONES FUNDAMENTALES DE LA HIDROSTATICA
Considérese el elemento de volumen mostrado en la figura 3. Se encontrará la consecuencia de imponer la condición de equilibrio traslacional sobre las fuerzas (que la sumatoria de todas las fuerzas de superficie actuantes sea nula) dirigidas a lo largo del eje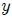 
.
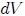.Al aplicar la condición de equilibrio traslacional sobre el eje 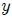resulta,
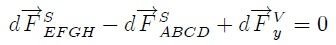
Ahora, indicando con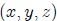 
las coordenadas de la cara 
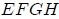, con 
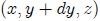las coordenadas de la cara 
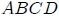y teniendo presente la ecuación 1, la ecuación 5 se puede escribir como,
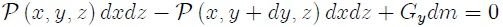
y debido a que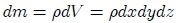 
(
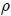es la densidad del fluido) entonces,
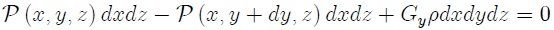
que depués de unos cambios triviales puede ser reescrita como,
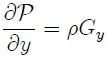
Procediendo de manera análoga con los otros dos ejes, se obtiene,
que son las denominadas Ecuaciones Fundamentales de la Hidrostática y es un conjunto de ecuaciones diferenciales.
TEOREMA DE PASCAL
En el caso particular de que 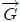provenga de un campo conservativo se cumple que,
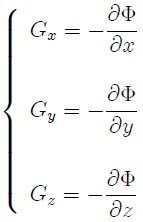
donde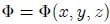 
es la función potencial (energía potencial 
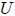por unidad de masa) que se expresa mediante,
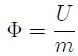
Las ecuaciones fundamentales de la hidrostática (sistema de ecuaciones 8), usando la ecuación 9, pueden ser escritas ahora como,
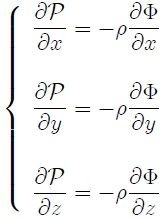
Estas ecuaciones permiten encontrar la diferencia de presión existente entre un punto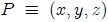 
y un punto 
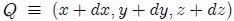en términos de la variación correspondiente de 
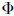de la siguiente manera,
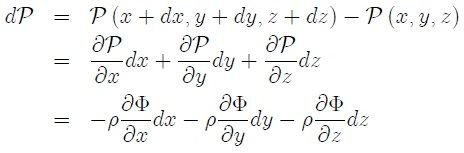
de donde,
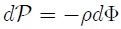
En el interior de un fluido homogéneo (densidad constante), la diferencia de presión entre dos puntos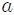 
y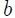 
a distancia finita puede ser obtenida integrando la ecuación 12 como sigue,
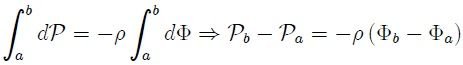
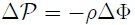
concluyéndose que,
Para una fuerza de volumen conservativa y un fluido homogéneo, las superficies isobáricas (de igual presión) 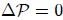 coinciden con las superficies equipotenciales (de igual potencial)  . |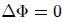
|---|
A partir de la ecuación 13 se deduce que: en un campo conservativo la diferencia de presión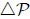 
entre dos puntos de un fluido homogéneo en reposo, depende de la diferencia de potencial 
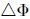de la fuerza de volumen entre dichos puntos. Pero 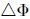depende sólo de las coordenadas espaciales y por lo tanto, en particular, no depende de la fuerza de superficie, por consiguiente ninguna presión adicional puede hacer variar 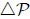. En otras palabras, el fluido realiza una transmisión hidráulica total de la presión ejercida sobre su superficie. Lo anterior constituye el denominado Teorema de Pascal que se enuncia así,
TEOREMA DE PASCAL: en un fluido homogéneo en reposo (líquido o gas), un incremento de presión producido en uno cualquiera de sus puntos se transmite inalterado a cualquier otro punto del mismo. |
|---|
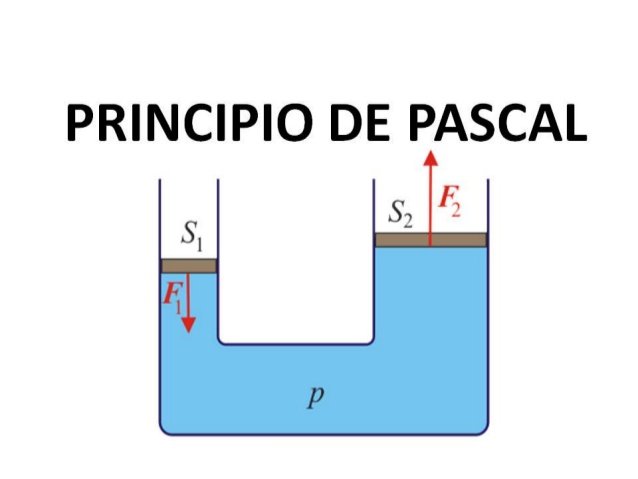
Existen numerosos aparatos que aprovechan el Teorema de Pascal, entre ellos está la máquina llamada Prensa Hidráulica. Esta máquina constituye la aplicación fundamental del mencionado teorema y permite entender mejor su significado.
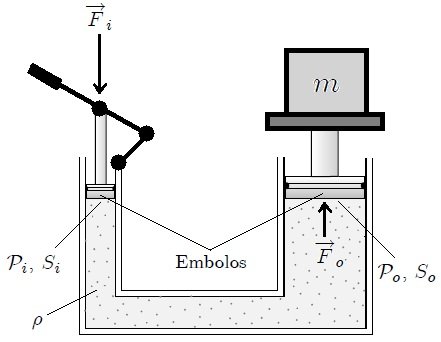
La Prensa Hidráulica (ver figura 4 es una máquina simple semejante a la conocida Palanca de Arquímedes, que permite amplificar la intensidad de las fuerzas y constituye el fundamento de elevadores, prensas, frenos y muchos otros dispositivos hidráulicos de la maquinaria industrial. Consiste, en esencia, en dos cilindros de diferente sección comunicados entre sí y cuyo interior está completamente lleno de un líquido que puede ser agua o aceite. |
|---|
Dos émbolos (o pistones) de secciones diferentes se ajustan, respectivamente, en cada uno de los dos cilindros, de modo que estén en contacto con el líquido. Cuando sobre el émbolo de menor sección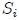 
se ejerce una fuerza 
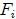perpendicular a la misma (el subíndice 
representa las cantidades de entrada), la presión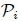 
que se origina en el líquido en contacto con él se transmite íntegramente y de forma instantánea a todo el resto del líquido (debido al Teorema de Pascal). Ahora, si las mismas cantidades se representan mediante el subíndice 
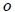(el subíndice 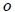representa las cantidades de salida) para el émbolo de mayor sección, es posible establecer que,
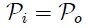
de donde al sustituir la ecuación 4 resulta,
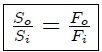
que es la Ecuación de la Prensa Hidráulica. A la cantidad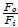 
se le denomina Ganancia Mecánica de la prensa hidráulica y es igual a la razón de las superficies de sus émbolos.
BIBLIOGRAFIA
Soldovieri, Terenzio. FISICA GENERAL - Una introducción a los Fluidos, Vibraciones y Termodinámica. 1era edición (borrador), 2017. Puede descargarse desde mi web http://www.cmc.org.ve/tsweb/
Mencuccini, C. & Silvestrini, V. FISICA I - MECCANICA E TERMODINAMICA, volume 1. Liguori Editore S.r.l., Napoli-Italia, 1988.
Balloffet, A.; Gotelli, L. M. & Meoli, G. A. HIDRAULICA, volume 1. Editorial EDIAR, Buenos Aires, 2da edition, 1952.
Serway, R. A. FISICA, volume 1. McGraW-Hill, Mexico, 4ta edition, 1997.
Yavorski, B. M. & Detlaf, A. A. MANUAL DE FISICA. Editorial MIR, Moscú, 1977.
Savéliev, I. V. CURSO DE FISICA GENERAL 1, volume 1. Editorial MIR, Moscú, 1984.
Espero que la anterior información les sea de mucha utilidad.
Hasta mi próximo post. ¡Saludos a todos! 😁.
Si deseas leer más artículos científicos de buena calidad, no pierda el tiempo, visite la etiqueta #steemstem. Es un gran proyecto que ha crecido enormemente en los últimos meses, con el fin de promover altos puestos a publicaciones científicas
Unete al canal de @steemstem. También puedes visitar el blog @steemstem y obtener mas información.
Qué información tan completa. Creo que me hará falta para explicarle algo a alguien, y por otra parte, creo que yo no habría tenido la paciencia para hacer esas imágenes en paint. ;) Un saludo.
Muchas gracias por tu comentario y apoyo @oscardice. Tengo habilidad con paint porque lo he usado por años para la edición de mis libros, los cuales puedes ver en mi web www.cmc.org.ve/tsweb
Ya te estoy siguiendo. Sígueme si es de tu agrado. Saludos!.
Excelente post, muy completo profesor
Muchas gracias @sainerc. Ya te estoy siguiendo. Sígueme si es de tu agrado. Saludos!.
Como ya nos tienes acostumbrados a tan buenas publicaciones. Felicitaciones y Saludos