¿Funciones matemáticas? Gráfica de una función básica.

[ycam]

¿Es una función matemática?

^{Criterios para la identificación de funciones básicas}

Las relaciones matemáticas parten de una igualdad matemática, pero en ocasiones no es suficiente argumento para catalogarla como una función matemática y podría ser tratada como una simple ecuación que relaciona varios parámetros específicos. Entonces veamos cuáles son los criterios más utilizados para poder identificar una gráfica como una función matemática.

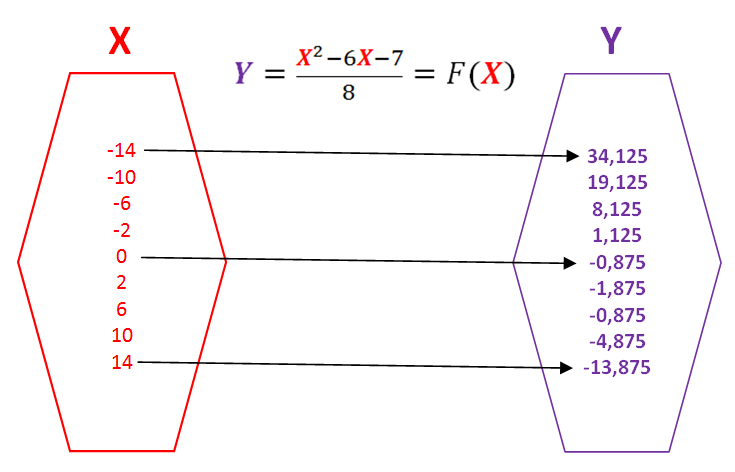
Como vimos en un ejemplo anterior "El análisis gráfico de las funciones de n-variables", podemos usar gráficos para representar una función. Para presentar estas figuras debemos comenzar a construir una tabla de valores con pares de entrada y salida en un rango finito de pares ordenados, de tal manera que la información visual que pueda brindar esta gráfica pueda facilitar la comprensión de la relación que estamos estudiando.

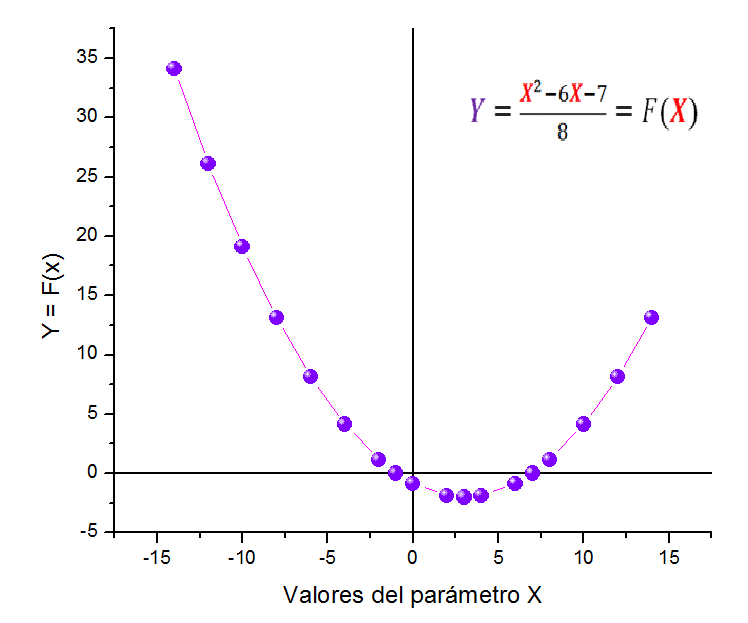
Por lo general, construimos gráficos con valores de entrada (parámetro X) a lo largo del eje horizontal y valores de salida (Y = F(X)) a lo largo del eje vertical. Por lo tanto, en esta publicación veremos que una de las maneras más rápidas y sencillas de determinar si estamos en presencia de una función matemática es a través del análisis de la gráfica de la función usando el criterio de la línea vertical en 2 ejemplos de igualdades matemáticas.

Ecuación 1:

Presento la ecuación general de una parábola que debemos expresarla en función de la variable Y, para luego ingresar los valores arbitrarios de X y realizar la gráfica Y = F(X): la primera observación es que el coeficiente del parámetro X² debe ser igual a 1, por lo que dividiremos toda la ecuación entre "2":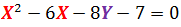

El procedimiento o metodología para realizar un análisis gráfico, consiste básicamente en lo siguiente: a) despejar la ecuación y reescribirla en términos de de la variable independiente, b) construimos una tabla de valores de entrada a la "máquina de funciones" y de salida en base a la relación Y = F(X), c) usamos un sistema de coordenadas con divisiones numéricas para representar cada par ordenado y finalmente unimos esos puntos.

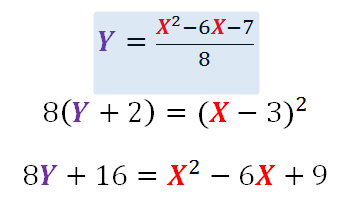
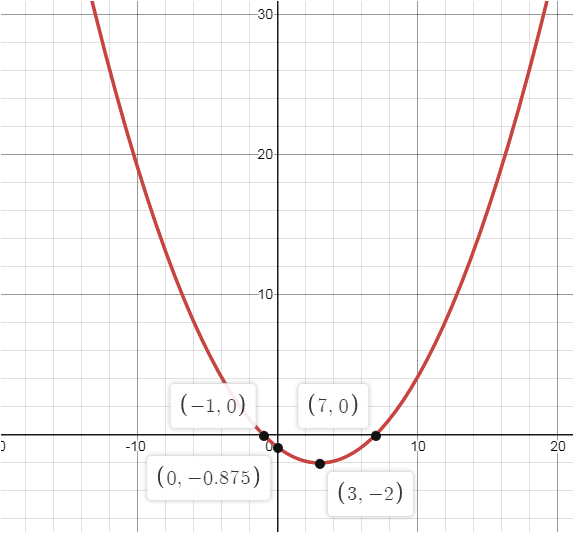
La expresión de arriba es otra manera de escribir la ecuación de una parábola, corresponde a la forma canónica, donde el par ordenado (h, k) representa el vértice de la parábola:

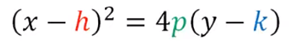
h = 3

k = −2

mientras que

p = 2

es un número positivo que indica que nuestra parábola de ejemplo abre hacia arriba.

Los puntos que resaltan aquí corresponden al par ordenado que corta al eje vertical en (0, −0,875), al eje horizontal tanto en (−1, 0) como en (7, 0), sin olvidar el vértice en el par ordenado (3, −2) representa el vértice de la parábola:

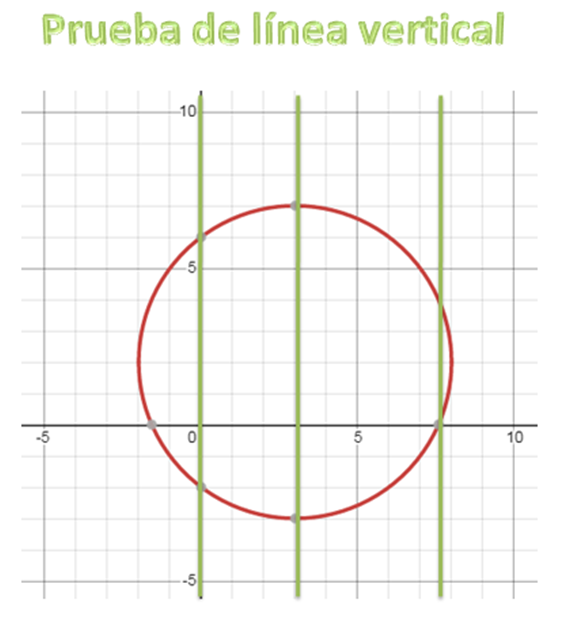
Prueba de la línea vertical:

consiste básicamente en trazar líneas perpendiculares al eje horizontal de las abscisas, de tal manera que: un punto en la gráfica de la función Y = F(X) tiene la forma (X, F(X)), así que una vez que se conoce la primera coordenada, se puede determinar la segunda coordenada, como lo hice en la construcción de la tabla de datos y que se correspondían 1 a 1, por lo tanto, es imposible que dos puntos en la gráfica de la función tengan la misma primera coordenada.

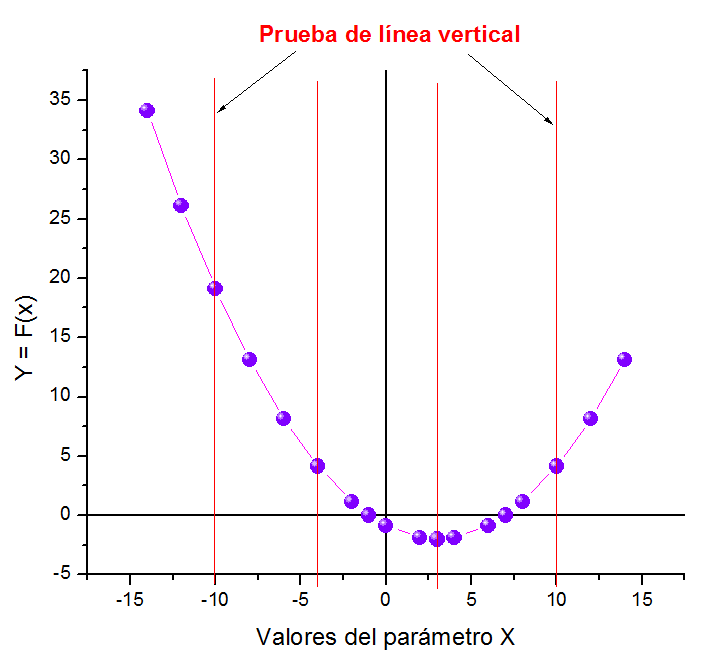
Lo anterior confirma que esta ecuación de una parábola representa una función matemática, puesto que cada una de las líneas verticales que pasan sobre los puntos (X_i, Y_i) sólo interceptan la gráfica Y = F(X) en un único punto.

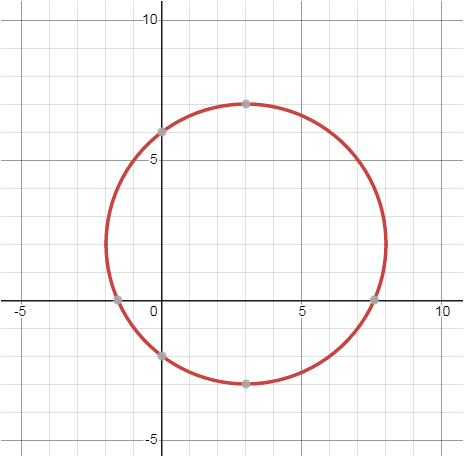
Analizando la ecuación de una circunferencia

Ya hemos visto que la prueba de la línea vertical aplicada en la gráfica de una parábola confirma que es una función cuyo "valor de resultado" se relaciona con un único "valor de ingreso". Ahora estudiaremos la ecuación de una circunferencia y analizaremos su gráfica para determinar si se trata de una función matemática o no, mediante esta prueba de línea vertical.

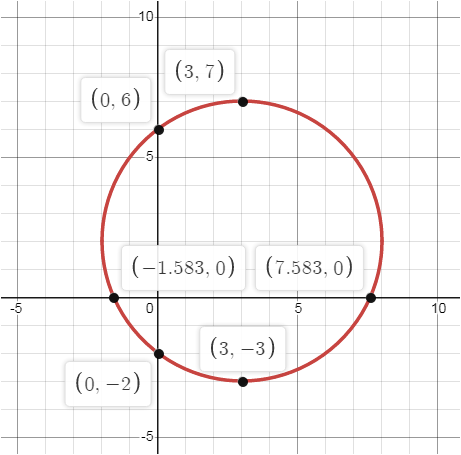
Ecuación 2:

Vamos a iniciar con la ecuación canónica de la circunferencia: (X − h)² + (Y − k)² = r² (h, k) es la coordenada del centro de la circunferencia r es el radio de la circunferencia

Un ejemplo sencillo para abordar el tema de verificación de funciones es el siguiente:

Con la ayuda de cualquier programa de computación podemos graficar los pares ordenados (X, Y): radio = 5 centro = (3, 2)

Ahora nos corresponde trazar líneas verticales para determinar la intercepción con la gráfica de la circunferencia.

Claramente se observa que la línea vertical (color verde) que hemos dibujado intercepta el borde de la circunferencia en 2 puntos distintos (simétricos), por lo que no hay una solución única para un valor de entrada "X", así que podemos concluir que Y no es una función de X.

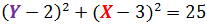
Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de pxfuel: Portada con el tema Funciones
• Guía de aprendizaje: Funciones y relaciones gráficas
• Vídeo: Graphing a Basic Function
• Video: Ecuación general y canónica de la parábola
• Wikipedia: Gráfica de una función

Las funciones matemáticas son expresiones que relacionan
las variables de una igualdad,
así que invariablemente encontraremos alguna solución

Comments

[steemstem]

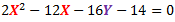
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!

Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).

Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support. 
 

[soy-venezuelien]

HOLA
Interesante, me gusto. Y me puso a investigar ya que soy ingeniero y pensaba lo contrario....

"Si a un valor de la variable x le corresponde más de un valor de y, entonces esa relación no es una función. ... Toda relación no tiene porqué ser necesariamente una función, aunque toda función sí que es una relación. Por lo tanto, una ecuación (que es una relación) no tiene que ser necesariamente una función"