Matemáticas sin secretos: Cálculo infinitesimal

[ycam]

Cálculo para modelar

^{Límite, derivada e integral}

El cálculo infinitesimal nos permite aproximarnos a valores tan cercanos a un suceso, por lo que es ampliamente utilizado en todas las ciencias básicas y la ingeniería para modelar cualquier tipo de fenómeno considerando un punto crítico de referencia o un rango de estudio establecido por los límites que se propongan. El tema que trataré en este artículo está relacionado con los límites, derivadas e integrales de funciones matemáticas simples y sencillas. Veamos algunos ejemplos y dos daremos cuenta que las Matemáticas sin secretos son aplicadas en este tipo de cálculo infinitesimal.

El límite de una función casi siempre estará acotado por un valor numérico, ya sea por la derecha o por la izquierda, y que tiende a devolver esa función cuando es evaluada con el valor de la abscisa que sea propuesto.

Suponiendo que la función propuesta para estudiar su tendencia cuando proponemos valores de interés para el analista:

F(n) = 5n² + 3n

El paso siguiente es proponer el valor de la abscisa

n → 4

y evaluar esta función cuando n tiende a 4, es decir que trataremos de hallar la tendencia de la función F(n) = 5n² + 3n

Evaluamos la función con un número real, siempre nos podemos aproximar infinitamente entre 2 números reales distintos, por ejemplo vamos a evaluar esa misma función cuando

n → 5

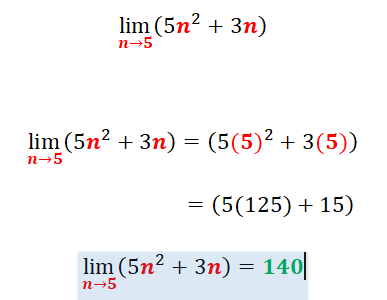
Lógica matemática:

vemos que la función evaluada cuando n → 4 y n → 5 dan como resultado valores diferentes, esa es la idea principal del estudio de los límites de una función, analizar la tendencia cuando evaluemos la función entre 4 y 5 veremos que existen infinitos resultados cada vez que cambiemos el valor límite, por ejemplo cuando n → 4,000001 o cuando n → 4,94903875495454854830938905854958545454548475983208390359, siendo los bordes de la función para cuando n → 4 el límite será 92 y para cuando n → 5, el límite será 140, mientras que entre estos 2 números 4 y 5 existirán valores infinitesimales cuando la función tienda a otros números intermedios.

Ahora, usemos esta misma función para determinar la derivada, siguiendo las reglas de la derivación que indicaré a continuación.

F(n) = 5n² + 3n

Si analizamos esta función para distintos intervalos de valores de n, podemos determinar si la función crece, decrece o es constante, para lo cual es muy importante tener en cuenta el concepto de pendiente de una curva. Por lo cual, al introducir el concepto de la derivada de una función, nos referiremos a la obtención de una nueva función que relaciona ese punto tangente a la curva, es decir su pendiente.

Considerando las reglas de la derivación y viendo que tenemos una potencia, entonces:

n^b = b·n^b−1

También, una constante (m) por la función: m·n^b = m·b·n^b−1

Obtenemos una nueva expresión para la función original.

Lo explico de manera corta, pero didáctica, la nueva expresión (función) dará como resultado el valor de la pendiente en el punto donde se evalúa la función original.

Sabemos que para n = 4, obtenemos F(4) = 92, así que si evaluamos la derivada F´(4) = 10(4) + 3 = 43 = m

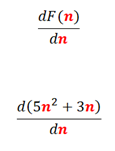
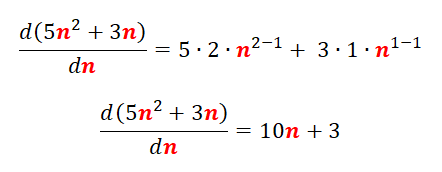
siendo el punto de tangencia: (X, Y) = (4, 92)

la pendiente en el valor de la abscisa n = 4: m = 43 de tal que debemos hallar la función que cumpla con estas condiciones. Luego,

Insertaré la gráfica para ayudarnos visualmente a ver el resultado de la derivada de la función original, esto es la recta tangente a dicha curva.

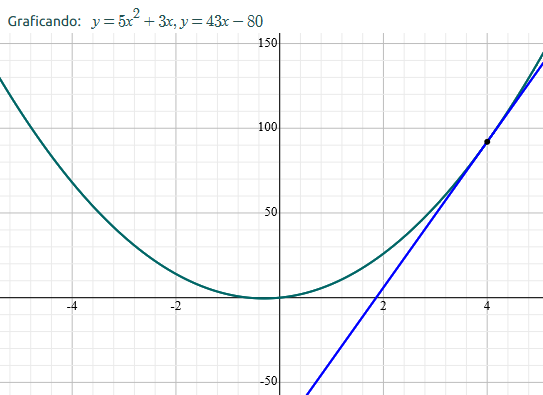
El siguiente punto del cálculo infinitesimal está referido al cálculo integral de la función. Buscando aproximar el área determinada por la función original, haciendo infinitas cálculos del área bajo la curva y sumarlos 1 a 1. Se tiene en cuenta que usaremos figuras geométricas para hacer que estas aproximaciones sean lo más precisas posible a la línea que limita dicha función.

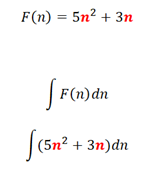
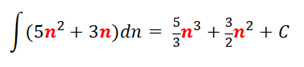
Así como existen las reglas de la derivación, también están las equivalentes a la integración de funciones. Cuando se tiene una potencia se le suma la unidad y además el resultado se coloca como divisor, veamos:

también:

Y además podemos evaluar esta integral dentro de un intervalo determinado, por ejemplo entre los valores de n = 4 (límite inferior) y n = 5 (límite superior):

Asignando actividades para el próximo lunes, los domingos no se estudia.

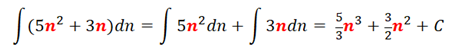
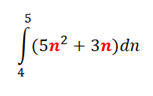
Apoyo bibliográfico y fuente de imágenes

Nuestra lógica y razonamiento matemático pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de jcoope12: Portada sobre Cálculo Infinitesimal
• Wikipedia: Límites
• Blog: Reglas derivación
• YouTube: Hallar la ecuación de una recta

El cálculo infinitesimal
nos acerca más y más
al valor real de un punto en el espacio

Comments

[ramonycajal]

Su post ha sido valorado por @ramonycajal

[stemsocial]

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!

Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).

You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.