No hay secretos en que si apostamos en juegos de envite y azar, existe una gran posibilidad de perder nuestros ahorros o tal vez multiplicar el dinero empleado en las apuestas. Ese espectro de dudas se despeja a partir de la estadística básica, calculando un valor porcentual relacionado con la frecuencia en la que ocurre algún evento.


En las estadísticas básicas se emplean expresiones matemáticas que tratan de analizar los experimentos aleatorios, tal como el lanzamiento de un dado para determinar la posibilidad de obtener un número par o lanzar cuatro monedas para calcular la probabilidad de obtener tres caras, siempre considerando la lógica matemáticacon un nivel jerárquico privilegiado.

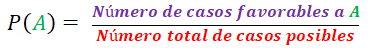
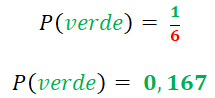


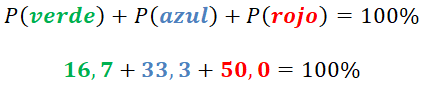



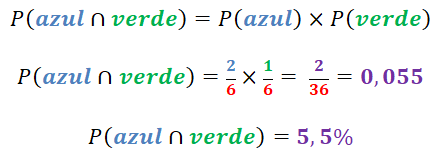

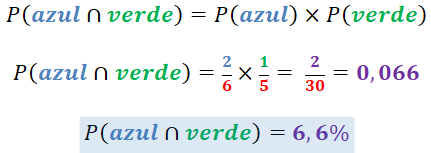
 ) = 16,7%.
Veamos otro evento de extracción, aprovechando este conjunto de esferas. ¿Cuál es la probabilidad de extraer una esfera de color
) = 16,7%.
Veamos otro evento de extracción, aprovechando este conjunto de esferas. ¿Cuál es la probabilidad de extraer una esfera de color  en el primer intento?
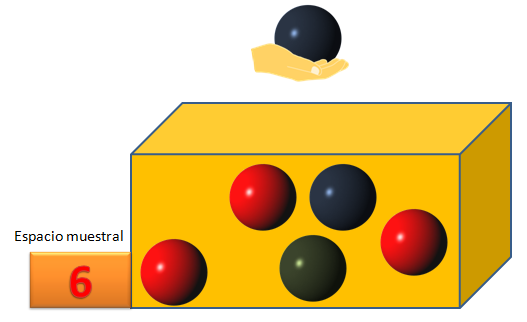
Note que la probabilidad de extraer una esfera de color azul se duplica en comparación con el ejemplo anterior, debido a que existen 2 esferas de color azul, así P(
en el primer intento?
Note que la probabilidad de extraer una esfera de color azul se duplica en comparación con el ejemplo anterior, debido a que existen 2 esferas de color azul, así P( ) = 33,3%. Si nos preguntan sobre la posibilidad de extraer una esfera de color blanco, entonces la P(blanco) = 0, porque sabemos que dentro de la caja no hay esferas de ese color en específico. Esto es lo que se conoce como un
¿Cuál es la probabilidad de extraer una esfera de color
) = 33,3%. Si nos preguntan sobre la posibilidad de extraer una esfera de color blanco, entonces la P(blanco) = 0, porque sabemos que dentro de la caja no hay esferas de ese color en específico. Esto es lo que se conoce como un
¿Cuál es la probabilidad de extraer una esfera de color  en el primer intento?
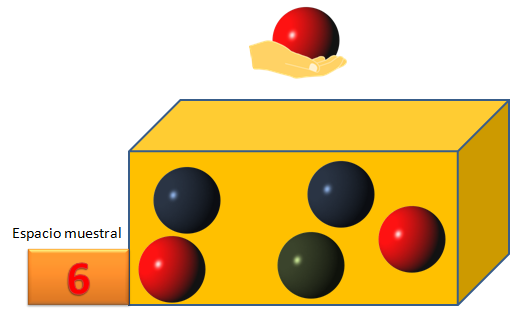
Cuando se habla de procesos aleatorios o eventos al azar, los relacionamos con juegos donde el resultado no lo conocemos y puede resultar cualquier cosa, así que sigamos "jugando" con este ejemplo. Preguntemos ahora, ¿cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color
en el primer intento?
Cuando se habla de procesos aleatorios o eventos al azar, los relacionamos con juegos donde el resultado no lo conocemos y puede resultar cualquier cosa, así que sigamos "jugando" con este ejemplo. Preguntemos ahora, ¿cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color  o extraer una esfera de color
o extraer una esfera de color  ?
¿Cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color
?
¿Cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color  regresarla a la caja y seguidamente extraer una esfera de color
regresarla a la caja y seguidamente extraer una esfera de color  ?
Finalmente, ¿cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color
?
Finalmente, ¿cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color  sin regresarla a la caja y seguidamente extraer una esfera de color
sin regresarla a la caja y seguidamente extraer una esfera de color  ?
?
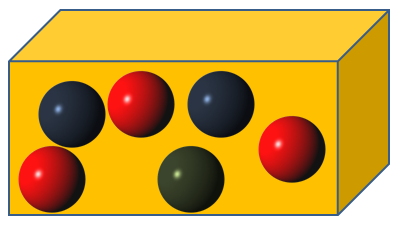
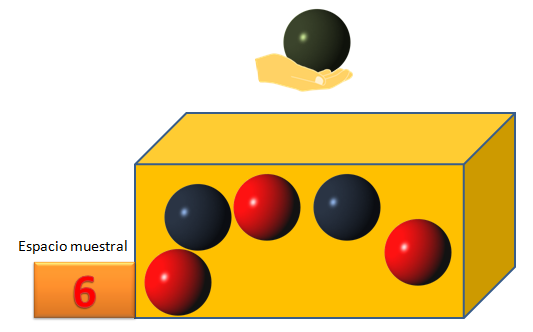
La posibilidad de que ocurra un suceso se relaciona con la frecuencia que un acontecimiento determinado se repita en un experimento aleatorio, a mayor frecuencia, mayor será la probabilidad que un suceso o evento ocurra.Este enunciado es más parecido a un artículo del código penal, mucho enredo literario, por lo que recurriré a un ejemplo sencillo para confirmar que sí es posible estudiar las Matemáticas sin secretos. Formulemos una situación real, como buscar una caja de cartón y colocar dentro de ella unas 6 esferas de colores:



¿Cuál es la probabilidad de meter la mano dentro de la caja y sacar una esfera de color
 en el primer intento?
en el primer intento?
La memoria histórica nos señala que fue Pierre Simon Laplace quien retoma las propuestas sobre eventos aleatorios y formula la Regla de Laplace, que relaciona la frecuencia relativa, después de repetir el evento aleatorio un número finito de veces, con la que ocurre dicho evento. Él propone la siguiente relación matemática:
 en el primer intento?
en el primer intento?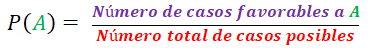
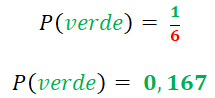





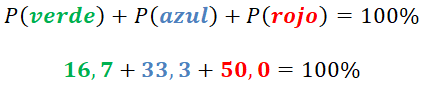



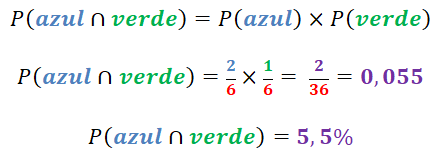

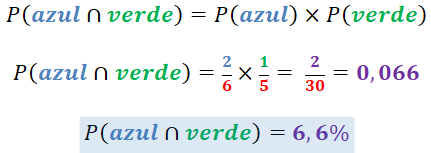
- Probabilidad de ocurrencia de un evento
- Suceso o evento
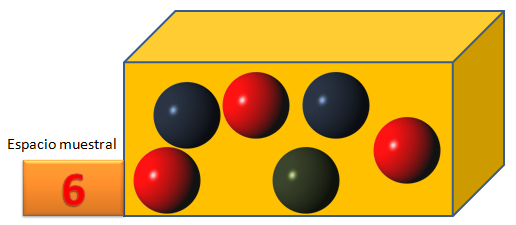
- Espacio muestral
- Regla de Laplace
- Unión e intersección de sucesos
Apoyo bibliográfico y fuente de imágenes
Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
- Imagen de geralt: Portada "Probabilidades"
- Blog: Probabilidad: conceptos básicos
- Blog: ¿Qué es probabilidad?
- Video YouTube: Regla de Laplace
 ) = 16,7%.
Veamos otro evento de extracción, aprovechando este conjunto de esferas. ¿Cuál es la probabilidad de extraer una esfera de color
) = 16,7%.
Veamos otro evento de extracción, aprovechando este conjunto de esferas. ¿Cuál es la probabilidad de extraer una esfera de color  en el primer intento?
Note que la probabilidad de extraer una esfera de color azul se duplica en comparación con el ejemplo anterior, debido a que existen 2 esferas de color azul, así P(
en el primer intento?
Note que la probabilidad de extraer una esfera de color azul se duplica en comparación con el ejemplo anterior, debido a que existen 2 esferas de color azul, así P( ) = 33,3%. Si nos preguntan sobre la posibilidad de extraer una esfera de color blanco, entonces la P(blanco) = 0, porque sabemos que dentro de la caja no hay esferas de ese color en específico. Esto es lo que se conoce como un
¿Cuál es la probabilidad de extraer una esfera de color
) = 33,3%. Si nos preguntan sobre la posibilidad de extraer una esfera de color blanco, entonces la P(blanco) = 0, porque sabemos que dentro de la caja no hay esferas de ese color en específico. Esto es lo que se conoce como un
¿Cuál es la probabilidad de extraer una esfera de color  en el primer intento?
Cuando se habla de procesos aleatorios o eventos al azar, los relacionamos con juegos donde el resultado no lo conocemos y puede resultar cualquier cosa, así que sigamos "jugando" con este ejemplo. Preguntemos ahora, ¿cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color
en el primer intento?
Cuando se habla de procesos aleatorios o eventos al azar, los relacionamos con juegos donde el resultado no lo conocemos y puede resultar cualquier cosa, así que sigamos "jugando" con este ejemplo. Preguntemos ahora, ¿cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color  o extraer una esfera de color
o extraer una esfera de color  ?
¿Cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color
?
¿Cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color  regresarla a la caja y seguidamente extraer una esfera de color
regresarla a la caja y seguidamente extraer una esfera de color  ?
Finalmente, ¿cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color
?
Finalmente, ¿cuál es la probabilidad de meter la mano dentro de la caja, extraer una esfera de color  sin regresarla a la caja y seguidamente extraer una esfera de color
sin regresarla a la caja y seguidamente extraer una esfera de color  ?
?
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations your publication has been chosen among the best of the day.
KEEP CREATING GOOD CONTENT.