Un Sistema de Álgebra Computacional (CAS por sus siglas en inglés Computer Algebra System) es un software que facilita las operaciones matemáticas y el cálculo simbólico, es decir, cálculos matemáticos usando valores simbólicos (variables y expresiones) en lugar de valores numéricos. Los CAS son de utilidad en todas las áreas de la matemática, por ejemplo en el cálculo diferencial e integral permiten calcular derivadas no solo de forma numérica sino también de forma simbólica, en este artículo se muestra un problema de aplicación de las derivadas en el cual se utilizaron dos Sistemas de Álgebra Computacional como ayuda en su proceso de solución.
En este caso de estudio se utilizaron los Sistemas de Álgebra Computacional Maxima y WolframAlpha, sin embargo, existen otros CAS en la actualidad que pueden usarse en este tipo de problemas. A continuación se muestra un problema de aplicación de las derivadas, específicamente de razones de cambio relacionadas:
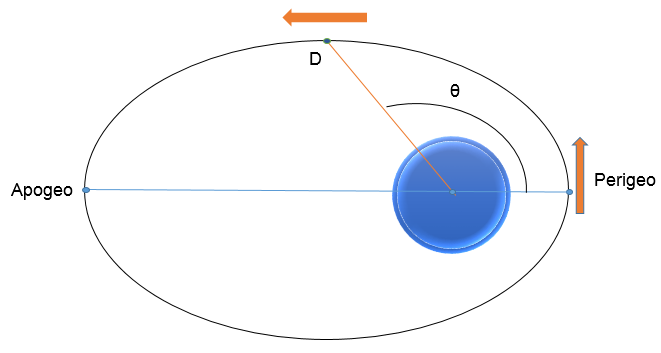
Imagen N° 1 Diagrama del Satélite orbitando alrededor de la tierra
Fuente: Elaboración propia
Un satélite artificial está en una órbita elíptica alrededor de la tierra. Su distancia r (en kilómetros) desde el centro de la tierra está dada por
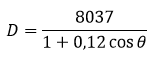
Donde θ es el ángulo medido desde el punto en la órbita más próximo a la superficie terrestre (ver la Imagen N° 1).
a) Determine la altitud del satélite en el perigeo (el punto más próximo a la superficie terrestre) y en el apogeo (el punto más apartado de la superficie terrestre), use 6378 Km para el radio de la tierra.
b) En el instante en que θ es de 120 grados, el ángulo θ aumenta a razón de 2,7 grados/min. Encuentre la altitud del satélite y la razón a la que esta cambia en este instante.
Solución:
Parte a) La altitud del satélite viene dada por la resta de la distancia al centro de la tierra y el radio de la tierra, es decir:
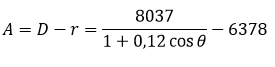
Para el perigeo se cumple que el angulo mide o° según se puede apreciar en la imagen N° 1, entonces
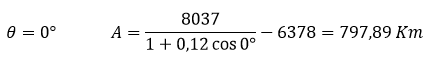
Para el apogeo el ángulo mide 180°, luego
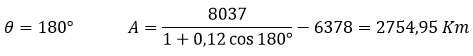
Parte b) En el instante en que θ es de 120 grados la altitud se calcula mediante la siguiente expresión:

En relación a la razón a la que cambia la altitud en el tiempo se trata de un problema de razones de cambio relacionadas, se debe determinar la razón a la que cambia la altitud en función del tiempo, expresando este hecho mediante derivadas se obtiene:
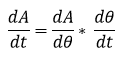
El valor al cual cambia el ángulo en función del tiempo, representa la siguiente razón de cambio
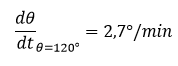
Se convierte la razón de cambio y el ángulo a radianes para poder trabajar usando las fórmulas de derivación generales
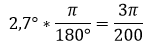
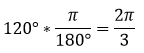
La razón de cambio
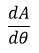
Corresponde a la primera derivada de la función altura por lo tanto
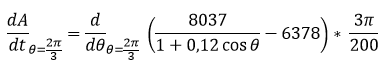
Utilizando máxima se resuelve la derivada mediante la siguiente expresión
diff((8037/(1+0.12*cos (x)))-6378,x,1);

Imagen N° 2 Resolución de la derivada utilizando Maxima
Fuente: Elaboración propia
La misma derivada puede resolverse usando WolframAlpha con el siguiente código
diff((8037/(1+0.12*cos (x)))-6378)
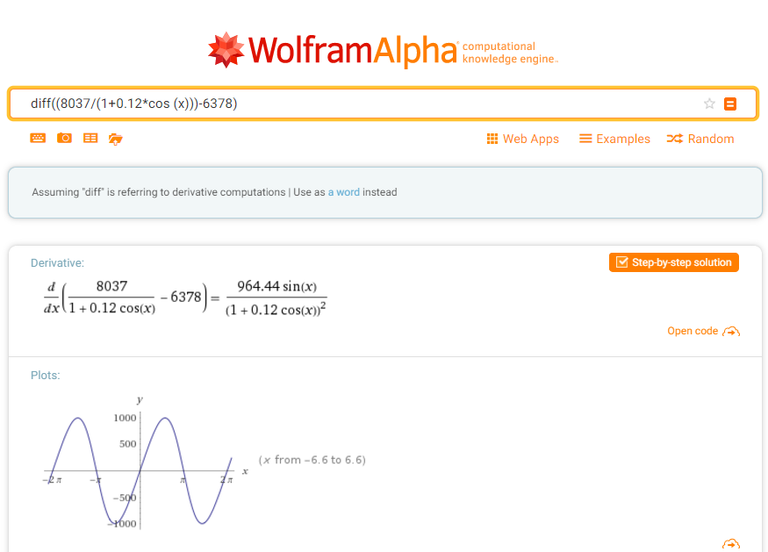
Imagen N° 3 Resolución de la derivada utilizando WolframAlpha
Fuente: Elaboración propia
Obteniendo
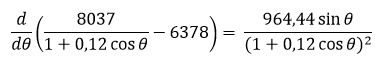
Sustituyendo en la formula que relaciona las dos razones de cambio se obtiene:
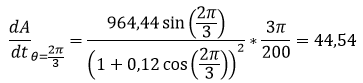
Por lo tanto la altitud del satélite cambia a razón de 44,54 Km por minuto, como es un valor positivo significa que en ese instante de tiempo el satélite se está alejando de la tierra.
En la resolución del problema anteriormente expuesto se evidenció la utilidad de los Sistemas de Álgebra Computacional al permitir resolver operaciones matemáticas de forma simbólica, sin embargo, es muy importante destacar que el arte del modelaje matemático solo puede ser realizado por los seres humanos, por lo tanto, se puede establecer que la tecnología por muy buena que sea si no está acompañada de los conocimientos necesarios para interpretar la realidad y convertirla en un modelo matemático no puede ser aplicada a problemas de la vida real.
Excelente información. Muy buen análisis. Te sigo.
Gracias por el apoyo.
Concuerdo contigo, por más que la tecnologia avance, ella no es nada sin el ser humano, al fin y al cabo, la misma es diseñada por nosotros.
Éxitos!
Gracias por el apoyo.
@ysmael gracias por la información. Excelente matemático saludos.
Muchas gracias.
Como siempre muy bueno tu análisis y el aporte de los CAS. Yo en la universidad lo usaba a menudo, aunque a veces el resultado que me mostraba era monstruoso y tenía que simplificar previamente varias cosas antes de pedirle la derivada ;)
44.54 km/min es lo mismo que 2672 km/hora, wow eso sí es velocidad, jeje. Un saludo.
Suele pasar que a veces no simplifican el resultado, aunque en los últimos años han evolucionado mucho en ese aspecto, gracias, Saludos desde Venezuela.
Excelente post! Muy interesante el tema, como siempre la calidad por delante :)
Gracias por el apoyo.
epale compa le metes de lleno a la matematica! me alegra eso porque es muy interesante que la apliques en la vida cotidiana
Ok, gracias por apartar algo de tú tiempo para leer el artículo.