El universo es un lugar fascinante que los científicos estudian todos los días descubriendo numerosos secretos en este proceso, a lo largo de los siglos la ciencia ha podido demostrar que el universo cumple leyes precisas, estas leyes pueden ser representadas mediante expresiones matemáticas.
Esta particularidad le otorga al universo observable propiedades que permiten describir el movimiento de los cuerpos celestes mediante ecuaciones y fórmulas, uno de los ejemplos más relevantes de este punto son las denominadas Leyes de Kepler las cuales pese a su simple enunciado tienen tras de si una amalgama de resultados matemáticos y astronómicos como base para su deducción, en el presente artículo se abordarán estas leyes y sus implicaciones en el movimiento de los planetas.
Johannes Kepler (1571-1630) estableció las tres leyes que en la actualidad llevan su nombre, estas leyes describen el movimiento de los planetas alrededor del sol (y más en general describen el movimiento de cualquier cuerpo celeste alrededor de otro), para deducir esta leyes Kepler se basó en los datos recopilados por el astrónomo Tycho Brahe (1546-1601) los cuales sirvieron de fundamento para enunciar sus famosas tres leyes.
Leyes de Kepler
1° Ley de Kepler
Todos los planetas giran alrededor del Sol, en este proceso describen órbitas elípticas. El Sol se encuentra en uno de los focos de la elipse.
La primera ley contradice la popular creencia de esa época la cual planteaba que la órbita de los planetas alrededor del sol formaba una circunferencia, Kepler no solo deduce que la excentricidad de las órbitas es suficiente para considerarla como una elipse, sino que también establece que el sol se encuentra en uno de los focos de dicha elipse.
Se debe recordar que una elipse según el Diccionario de la Real Academia Española se define como el:
Lugar geométrico de los puntos del plano cuya suma de distancias a otros dos fijos, llamados focos, es constante.
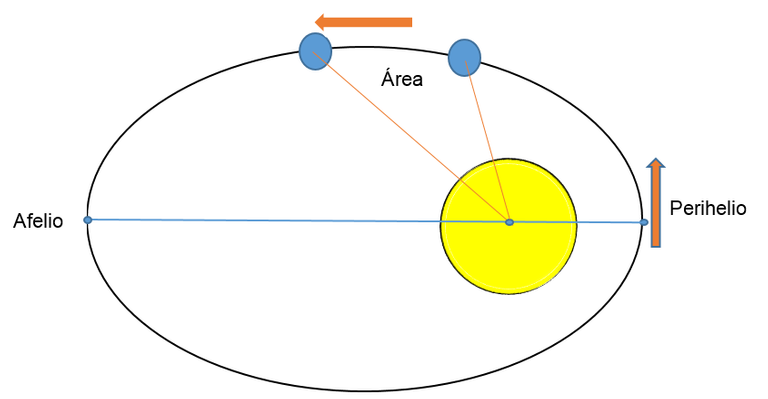
Imagen N° 1 Trayectoria elíptica de un planeta que gira alrededor del sol, Fuente: Elaboración propia
2° Ley de Kepler
El radio vector que une un planeta y el Sol recorre áreas iguales en tiempos iguales.
Como se observa en la imagen N° 1 esta ley implica que el planeta debe moverse más rápido cuando esta cerca del sol para que el área recorrida pueda ser igual a la que recorre cuando esta distanciado del sol, es decir, alcanza su velocidad máxima en el perihelio (punto donde se encuentra más cercano al sol) y su velocidad mínima en el afelio (punto más alejado del sol).
3° Ley de Kepler
El cuadrado del periodo orbital de los planetas alrededor del Sol es proporcional al cubo de la distancia media del planeta al Sol (ley de los periodos).

Esta última ley permite calcular el tiempo que tarda un planeta en dar la vuelta alrededor del sol en función de la distancia media a la que se encuentra del sol.
Sin embargo, una de las limitaciones de esta ley es que describe el movimiento de los planetas sin tomar en consideración las fuerzas que intervienen en dicho movimiento, a pesar de esto es fácil demostrar su relación con la ley de gravitación universal de Newton, la cual plantea que:
“Todas las partículas del universo se atraen entre sí con una fuerza directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia entre ellas. La dirección de esta fuerza es a lo largo de la línea que las une”
Este hecho se expresa como:
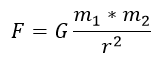
Donde G es la llamada constante de gravitación universal la cual tiene un valor de
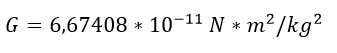
Teniendo en cuenta que la fórmula para calcular la aceleración centrípeta (aceleración dirigida hacia el centro) de un planeta que órbita alrededor de Sol es
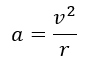
Donde v es la velocidad a la que se mueve el planeta la cual puede ser calculada mediante la siguiente expresión
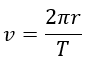
Sustituyendo v en la fórmula para la aceleración centrípeta, se obtiene
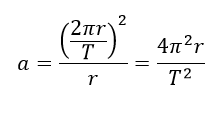
Recordando la segunda ley de Newton se puede establecer que
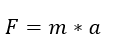
Como la masa del planeta se denota por m2
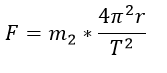
Esta expresión se puede igualar con la ley de la gravitación universal obteniéndose
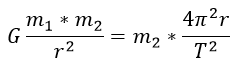
Simplificando
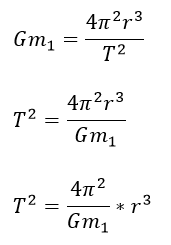
Que se corresponde con la tercera ley de Kepler donde la constante de dicha ley es igual a
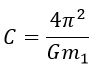
Con lo cual se puede apreciar la relación entre la tercera ley de Kepler y la ley de la gravitación universal (esta última aborda el movimiento de los planetas desde la perspectiva de las fuerzas que intervienen en dicho movimiento). Para el caso del Sol el valor de la constante C de la tercera ley de Kepler sería:
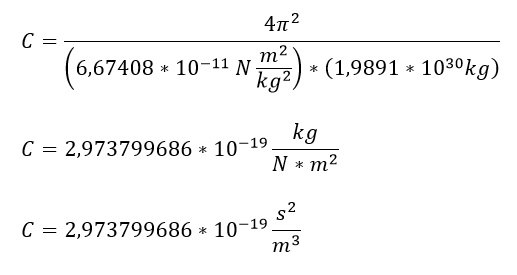
A partir de este valor se puede aproximar el periodo orbital de cada planeta del sistema solar en función de la distancia a la que se encuentre del sol, obteniendo los siguientes resultados:
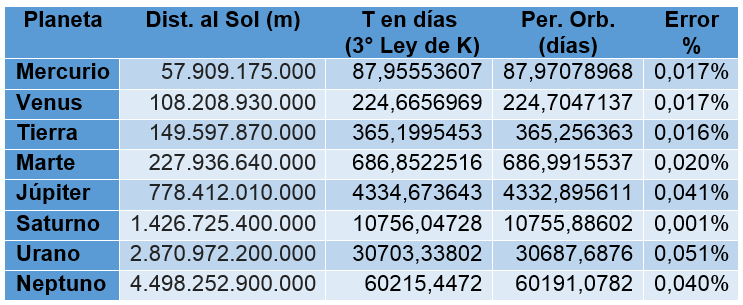
Tabla N° 1 Aplicación de la 3° Ley de Kepler y análisis del error porcentual. Fuente: Elaboración propia.
Como se puede apreciar en la tabla N° 1 para los 8 planetas del sistema solar los valores generados por la tercera ley de Kepler se aproximan bastante a los valores reales de los periodos orbitales de cada planeta. Sin embargo, la aplicación de las leyes de Kepler no se limita a los planetas que giran alrededor del sol, aplicándola al sistema binario Plutón-Caronte se obtienen los siguientes valores, (la masa de Plutón es 1,25 *1022Kg)

Como Caronte orbita a una distancia de 19.570 km de Plutón se cumple que
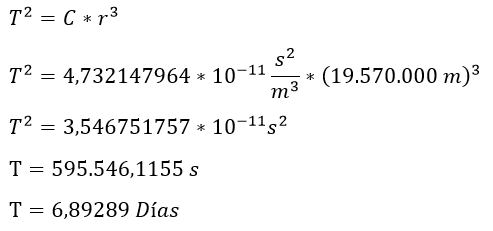
Lo cual se aproxima al periodo orbital de Caronte en torno a Plutón 6,387 días. Las leyes de Kepler pese a su simplicidad permitieron describir de forma adecuada el movimiento de los cuerpos celestes y la duración de sus periodos orbitales y sentaron las bases para la ley de la gravitación universal de Newton, sin embargo, en la presencia de campos gravitatorios fuertes (como en las cercanías del sol), tanto las leyes de Kepler como la gravitación universal de Newton resultan insuficientes para explicar el comportamiento de los planetas.
Un ejemplo histórico de esta situación es el problema de la precesión del perihelio mercurio, este movimiento implica que el eje de la órbita elíptica de mercurio alrededor del Sol gira 42.98 segundos de arco por siglo, las teorías sobre el movimiento de los planetas en el momento en que se descubrió este hecho eran insuficiente para explicar el porqué de la precesión de Mercurio, sin embargo, cuando Albert Einstein público su teoría general de la relatividad abordó este problema resolviendo uno de los dilemas científicos más importantes del momento.
CONCLUSIONES
- El movimiento de los planetas en el universo sigue leyes precisas que pueden ser representadas mediante expresiones matemáticas permitiendo calcular con precisión sus trayectorias.
- Las leyes de Kepler representan un antecedente importante a la ley de la gravitación universal de Newton, sin embargo, los resultados de esta dos teorías son generalizados en un modelo más preciso con el descubrimiento la Teoría General de la Relatividad de Einstein.
BIBLIOGRAFíA CONSULTADA
Bernardini (2004), Leyes de Kepler. Disponible en http://www.astrosurf.com/astronosur/docs/Kepler.pdf
Diccionario de la Real Academia Española (2014). 23° Edición. Disponible en http://www.rae.es/
Martin (2003), Física General. Disponible en http://fisicas.ucm.es/data/cont/media/www/pag-39686/fisica-general-libro-completo.pdf
Paredes y Romero (2014) Las leyes de Kepler y la ley de la gravitación universal. Disponible en http://casanchi.com/fis/keplerguniversal01.pdf
Resnick, Halliday y Krane (1993), Física. 3ra edición Compañía Editorial Continental México Volumen 1.
Felicitaciones.Claro ejemplo de los aportes de la investigación racionalista. Muy buen post @ydavgonzalez
Así es estimado @tomastonyperez un ejemplo de como evoluciona nuestra compresión del universo.
Congratulations @ydavgonzalez! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPme recuerda que kepler debe ser conquistado para preservar la raza humana!
Se ha teorizado mucho sobre ese planeta Kepler-22b, Saludos @calabzocriollo.