Probabilidad en los caminos aleatorios
La distribución normal en la distribución de caudal de agua
Cuando terminé de redactar mi última publicación vino a mis recuerdos un problema sencillo sobre distribución gaussiana aplicada en tuberías de agua y la probabilidad de unión de los caminos aleatorios que pueda tomar un caudal de ese líquido.

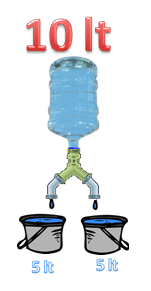
P[izquierda] = 1/2 = 0,5 en porcentaje = 50%
el 50% de 10 litros serían los 5 litros indicados en la imagen
P[derecha] = 1/2 = 0,5 en porcentaje = 50%
los otros 5 litros que se muestran a la derecha de la figura anterior.
V[izquierda] = 10 litros
V[derecha] = 10 litros
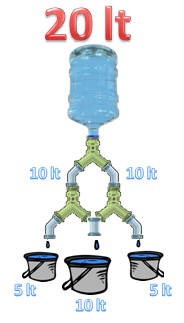
P[izquierda] = 1/4 = 0,25 en porcentaje = 25%
P[centro] = 2/4 = 0,5 en porcentaje = 50%
P[derecha] = 1/4 = 0,25 en porcentaje = 25%

P[izquierda] = 1/8 = 0,125 en porcentaje = 12,5%
12,5% de 20 litros son 2,5 litros que llegan en el recipiente de la izquierda.
P[centro-izquierda] = 3/8 = 0,375 en porcentaje = 37,5%
P[centro-derecha] = 3/8 = 0,375 en porcentaje = 37,5%
P[derecha] = 1/8 = 0,125 en porcentaje = 12,5%
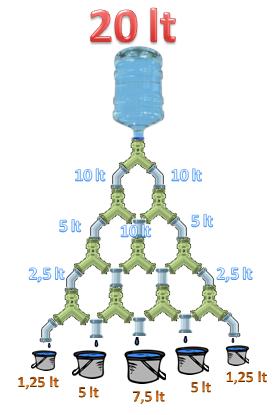
P[centro] = 6/16 = 0,375 en porcentaje = 37,5%
por regla de 3: si 20 litros son el 100%, entonces 7,5 litros serán
37,5%

Supongamos que en una lavandería industrial se desea distribuir un caudal de agua hacia diversos tanques para ser usados posteriormente en lavadoras de diversas capacidades de carga de ropa, así que se utilizan las conexiones entre las tuberías de igual diámetro interno. La intervención del cálculo matemático se basa en la probabilidades de un evento, tal como lo vimos en la publicación Caminos aleatorios en la Máquina de Galton, pero vamos a partir con el caso sencillo de un botellón de agua de 10 litros que se coloca con la boquilla abierta hacia abajo y conectada a una tubería tipo Y (bifurcada). En los 2 extremos se colocan baldes para capturar el agua y medir su volumen (capacidad) en litros.

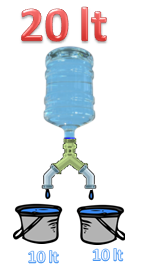
¿Qué sucede si en lugar de 10 litros sean 20 litros? Los cálculos de la probabilidad sería en base al 50% para cada recipiente de agua y el volumen que llena cada recipiente sería:

Hagámoslo más complejo agregando más tuberías en Y, con el mismo diámetro interno para no privilegiar las probabilidades de ocurrencia de un evento.

La clave en este tipo de situación es que cada tubo en Y divide el flujo a la mitad del caudal de entrada, por lo que la salida puede calcularse como una probabilidad
Pregunta: ¿por qué 1/4 y 2/4?
, es válido cuestionar la aparición del denominador número 4, causa dudas debido a que tenemos 3 tobos para el agua, otros dirán que es razonable porque existen 4 orificios de salida en los 2 tubos Y, pero la lógica matemática sugiere que el flujo de entrada debe dividirse entre 2.
Coloquemos otra fila de tubos Y para analizar la nueva situación:

A medida que vayamos colocando filas de nuevas tuberías Y, los cálculos de probabilidades en los recorridos aleatorios se van haciendo mayores los denominadores, porque el caudal de entrada se divide a la mitad en el orificio de salida, así: (1/4)/2 = 1/8
Finalmente le agregamos otra fila a la distribución de tuberías para nuestra lavandería industrial hipotética y se nos va a parecer al ejemplo de laMáquina de Galtonque les presenté ayer, con 5 casillas numeradas y aquí tenemos 5 recipientes que almacenarán el agua disponible para las lavadoras.

Nuevamente aparece la relación con el 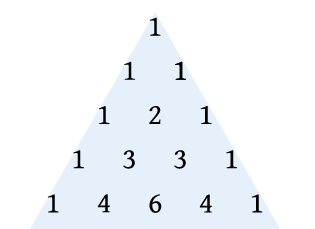
Triángulo de Pascal
, considerando hasta la quinta fila, o cuántos recipientes de agua tengamos disponible:

Apoyo bibliográfico y fuente de imágenes
Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
- Imagen de Antoine Taveneaux: Portada: Probabilidad en los caminos aleatorios
- Wikipedia: Distribución normal
- Wikipedia: Triángulo de Pascal
- Imagen de Drini: Figura del triángulo de Pascal
Congratulations @ycam! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
Your next target is to reach 800 replies.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
¡Felicitaciones!
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
3. Suscríbete a nuestra COMUNIDADEntra aquí para más información sobre nuestro trail., apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
4. Creación de cuentas nuevas de Hive aquí.
5. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA