StemQ Notice: The following is an answer to this question
General version of the problem
I am going to answer this question in a more general form. Denote by R the radius of the sphere , by c the rate constant of evaporation, and denote by h the height of the water level with respect to the bottom of the semi-spherical cup. So R,c will be constants but h will be a variable, more specifically, a dependent variable and the independent variable is of course time which I will denote by t. Then, the aim is to find a formula for h(t).
Overview
Here is an image of the whole setup:
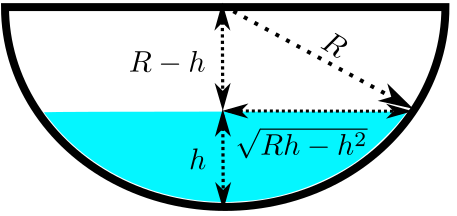
I did a bit of geometry in the image. This might help readers which want to write out all the details of the equations that will follow.
Equations
The surface area of the water at water level h is a function of h so let's denote the area by A(h). The water-volume at water level h can also be written as a function h so denote the volume by V(h). With some basic (and tedious) calculus we can write formulas for both:

Then the equation which relates the volume to the area is given by:
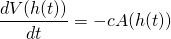
This is a first order differential equation. Straightforward computation using pretty basic calculus yields the solution h(t) = h(0) - ct (where h(0) is the water level at t=0). Observe that the equation is elegant in the sense that it is very simple. This is pretty cool.
Note that the equation only makes sense for h(t) greater or equal to zero. More specifically, when h(t)=0 all the water has evaporated.
Intuition
Intuitively, the solution formula h(t) = h(0) - ct makes sense since even without doing any calculus we expect that V(h) ~ c_1 h^3 and A(h) ~ c_2 h^2. So then according to the differential equation h(t) ~ c_3 t.
The result without equations
Stripping the math from this blog post our final results tells us that the water level goes down at a constant speed. :o)
StemQ Notice: This post was originally submitted on StemQ.io, a Q&A application for STEM subjects powered by the Steem blockchain.
Is that an african or a european spherical cup?
You can swallow water from an African cup quicker :P
Posted using Partiko Android
Ok, that was a good one
Does it matter? 😀
It's clear you skipped your monty python class at school :(
SHAZAM: called by @mathowl
Swallow related question so need some bird votes here @regularowl
Posted using Partiko Android
So the rate at which the water level drops is independent of the shape of the receptacle.
No matter what differences between the shapes of two containers, as long as the initial height of liquid is the same both will have their content fully evaporated in the same amount of time.
Interesting!
I suppose when thinking about it it makes sense since each area unit will cause the column of water beneath it to decrease at a rate independent of all other area units.
Thanks! 😀
That is a nice way of summarising the results :)
Posted using Partiko Android
This post has been voted on by the SteemSTEM curation team and voting trail.
If you appreciate the work we are doing, then consider supporting our witness stem.witness!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider setting @steemstem as a beneficiary to your post to get a stronger support.
Please consider using the steemstem.io app to get a stronger support.
Hi @mathowl!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your UA account score is currently 3.714 which ranks you at #4996 across all Steem accounts.
Your rank has improved 434 places in the last three days (old rank 5430).
In our last Algorithmic Curation Round, consisting of 190 contributions, your post is ranked at #46.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by mathowl from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.