Saludos a todos, les doy la más cordial bienvenida a mi blog. Hoy les voy a explicar la suma de fracciones.
Pero, ¿qué es una fracción?
En primer lugar, una fracción es un objeto matemático que posee dos partes: el numerador, el cual es el número que está sobre una raya de fracción, y el denominador, es el número que está debajo de la raya de fracción"; es importante destacar que el denominador debe ser diferente de 0.
Una fracción tiene la forma de a/b donde a y b son dos números reales tales que b≠0
• Como por ejemplo tenemos los siguientes: 1/2 y 3/4
El número que esta sobre la raya de fracción se llama ''numerador'' y nos representa el todo que vamos a dividir en partes iguales, el número que está debajo de la raya de fracción es el ''denominador'', este nos dice en cuántas partes vamos a dividir ese todo.
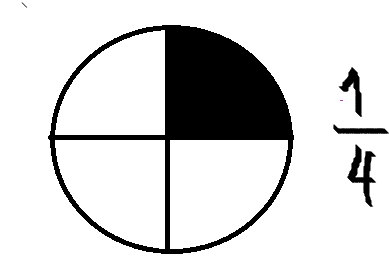
Veamos en la imagen que el todo se ha dividido en 4 partes iguales, de esas partes se ha seleccionado una, la cual queda representada como ¼, es decir, de las 4 partes en que hemos dividido al ‘’todo’’, y de esas partes se ha tomado una.
Existen dos tipos de fracciones, ellas pueden ser: propias e impropias.
Las fracciones propias tienen un numerador menor que el denominador, mientras que las impropias tienen un numerador mayor o igual al denominador."
He aquí un ejemplo de una fracción impropia:
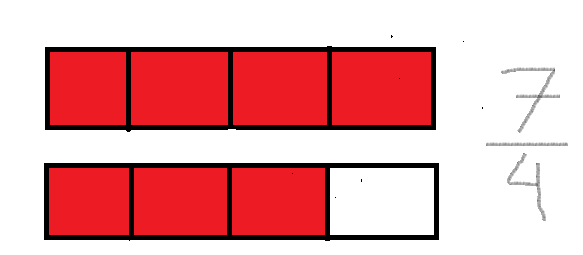
Y aquí un ejemplo de una fracción propia

También tenemos las fracciones mixtas y las fracciones equivalentes.
Una fracción es mixta si se puede expresar como una fracción impropia y a su vez como la suma de un numero entero más una fracción propia.
En la siguiente imagen conseguimos un ejemplo:
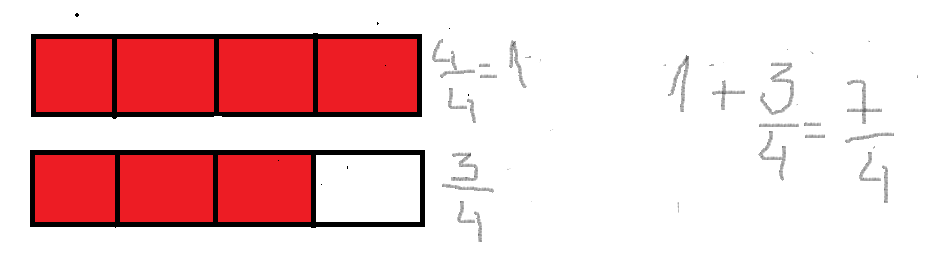
Observación:
Más adelante explicaremos con ejemplos las fracciones mixtas.
A continuación, hablaremos acerca de las fracciones equivalentes.
Dos fracciones: a/b y c/d son equivalentes si y solo si se cumple que a.d=b.c
A continuación, mostramos algunos ejemplos:
4/3 y 20/15 son equivalente ya que 4.15=3.20.
Esto es: 60=60
(-7)/2 y (-21)/6 son equivalentes ya que-7.6=2.(-21)
En ambos lados de esta igualdad,el resultado es-42.
1/2 y 3/4 no son equivalentes ya que el producto 1.4=4 y el producto 2.3=6
A continuación, vamos a sumar fracciones.
Pero, primero hablemos de dos tipos de fracciones especiales, ellas son:
La Fracción Nula
La Fracción Nula es aquella fracción cuyo numerador es 0 y su denominador es cualquier número real distinto de 0.
Esta fracción se identifica con el número real 0.
Esto es: 0/b=0,donde b es diferente de 0.
Ejemplos: 0/2=0
0/(-4)=0
La Fracción Unidad
La Fracción Unidad, es una fracción cuyo numerador y denominador son iguales.
Esta fracción se identifica con el número real 1.
Esto es: a/a=1,donde a es diferente de 0.
Ejemplos: 3/3=1
(-4)/(-4)=1
Comencemos con la suma de fracciones:
Al sumar fracciones se pueden presentar dos casos:
El primero:
Sumar fracciones con el mismo denominador
En este caso, simplemente se suman los numeradores de acuerdo al signo, es decir, se realiza la suma algebraica de los numeradores y se repite el mismo denominador.
Esto es:
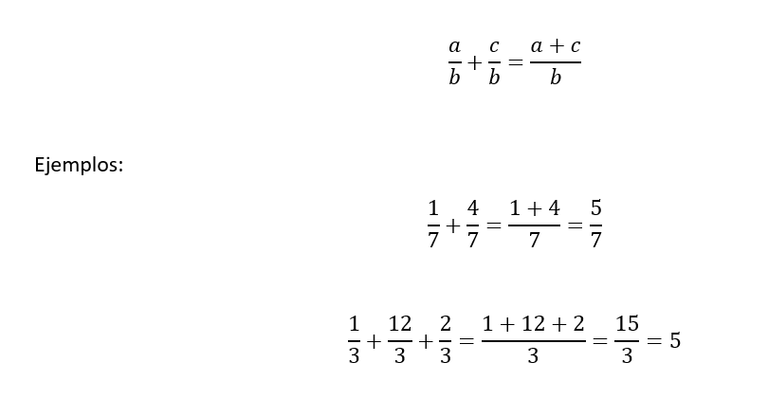
Esta regla para sumar fracciones también es válida para la diferencia de fracciones:
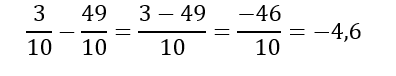
Y en general, para la suma algebraica de fracciones con igual denominador:
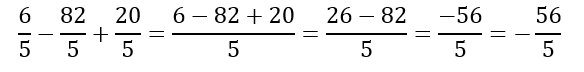
Para sumar o restar fracciones con diferentes denominadores se procede mediante la siguiente regla:
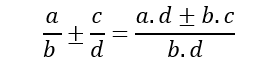
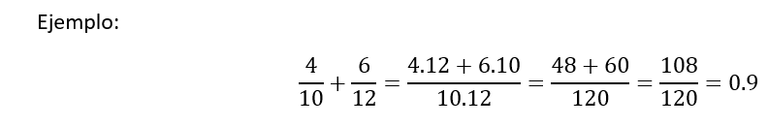
Pero, ¿existe otro procedimiento para esta operación?
Si existe otro procedimiento, y es el siguiente:
Primero se busca el mínimo común múltiplo (m.c.m) entre los denominadores de las fracciones que estamos sumando.
Veamos:
Sigamos con el ejemplo anterior:
Identifiquemos los denominadores y busquemos el m.c.m entre 10 y 12.
Así:

Para obtener el mínimo común múltiplo entre los denominadores, lo que hacemos es multiplicar todos los factores primos que se encuentran en la última columna.
Eso es:
El m.c.m (10 y 12) =2.2.3.5=60
Copiamos nuestro ejercicio anterior y lo igualamos a una nueva fracción cuyo denominador es 60, y luego procedemos de la siguiente manera:
Dividimos 60 entre cada denominador de los sumandos dados, y el resultado de esa división se multiplica por el numerador respectivo:
Así:
60÷10=6 →6.4=24
60÷12=5→5.6=30
Estos dos resultados van sobre la raya de fracción de la nueva fracción, finalmente se efectúa la suma algebraica, así:
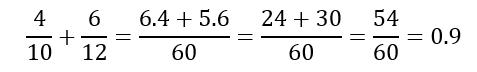
Aquí verificamos que nos da el mismo resultado que con el procedimiento anterior.
Y de estas dos formas podemos sumar o restar fracciones con distinto denominador.
Veamos algunos ejemplos misceláneos.
Efectué las operaciones siguientes:
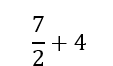
En ejercicios de sumas de este tipo, se multiplica el entero por el denominador de la fracción y el resultado se suma con el numerador respectivo, así:
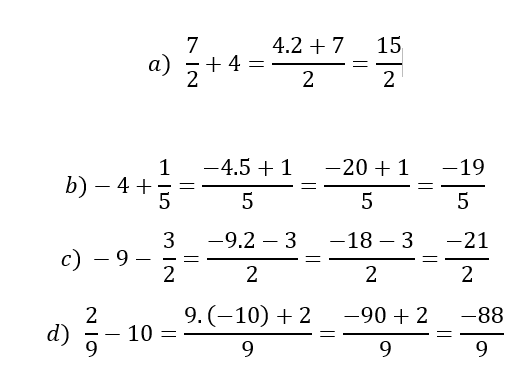
Cuando se nos presenta una expresión como esta, estamos ante un numero mixto:
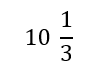
Y, ¿a cuánto equivale ese número mixto?
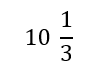
equivale a 10 unidades enteras sumadas con 1/3
Esto es:
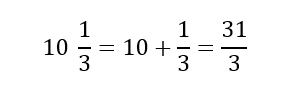
Es decir, que un número mixto equivale a la suma de su parte entera con su parte fraccionaria.
Es decir que:
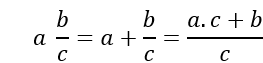
Bueno amigos, espero que les haya resultado útil este post.
Hasta una próxima oportunidad.
Créditos:
Este post es totalmente original de la autora.
¡Felicitaciones!
Estás participando para optar a la mención especial que se efectuará el domingo 6 de abril del 2025 a las 8:00 pm (hora de Venezuela), gracias a la cual el autor del artículo seleccionado recibirá la cantidad de 1 HIVE transferida a su cuenta.
¡También has recibido 1 ENTROKEN! El token del PROYECTO ENTROPÍA impulsado por la plataforma Steem-Engine.
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
2. Contáctanos en Discord: https://discord.gg/hkCjFeb
3. Suscríbete a nuestra COMUNIDADEntra aquí para más información sobre nuestro trail. y apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
4. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.