
During 25 years of teaching experience I have heard this phrase in the mouths of my students at the beginning of a course. This concern caused me, during that time, to investigate the reasons that originate it and consequently refine my applied techniques in the teaching and learning process. For this research I used surveys and interviews, in addition to some bibliographical references.
This article is the beginning of a series that intends that gradually the reader can acquire tools for simple learning in the area of Mathematics.
Below I will list some of these reasons, and I will direct this article to a general audience: students, teachers and people who generally like this topic.
Reason #1: The symbology and its meaning.
Mathematics is understood by means of symbols, for example, numbers are written symbols that indicate quantities, that is, without understanding the meaning of the symbol it is difficult to decipher the content of some problem raised with the use of these symbols. Something similar happens when we want to understand a language different from the one we use in a natural way.
Try to list on a sheet of paper all the Mathematical symbols that you remember and their meaning. It could take a big surprise.
Reason #2. Redaction of the problem.
If the problem is written in the student's native language, it is usual to find words such as: solve, find, demonstrate, and others, which involve a mathematical technique to be used to find the solution to the problem. If the student is not clear with the use of these words in the mathematical environment then he will not know what to do with it. Another difficulty scenario appears when the problem is written in a foreign language, this difficulty is obvious. Another difficulty is that which occurs when in the writing it is customary to substitute words from the native language with logical symbols: an expression such as "there exists an unique" is replaced by an inverted letter "E" and next to it an "!".
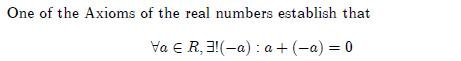
Reason #3. Understanding and Memorization.
It is not enough to recognize the symbol read, it is necessary to understand it in the environment in which it is being used. In addition, it is necessary to memorize the symbol and its meaning. Just as the repetition of the words in the native language, either by reading or writing, they are memorized until they achieve a good spelling and use of them, in the same way it happens with mathematical terms or symbols.
Look for a Math book and try to list the symbols you have read and copy their meanings. Read it once, close your eyes, and try to repeat them from memory.

Reason #4. Natural Skills.
Among all the skills or abilities to do something easily we have some innate, and others that are acquired with the repetition of some technique. The vast majority of tests that measure the IQ of a person separate their measurements in terms of the modality of reasoning: verbal, abstract, mechanical, etc. In mathematics the modality of abstract reasoning is quite necessary. There are people who have developed these skills very easily. Those people who have difficulty could acquire it by solving certain exercises that stimulate the development of this ability.
In general, abstract reasoning can be developed by means of images, through music, by the association of an idea with a symbol. Although it may seem a lie, assembling puzzles, reading scores, associating a painting with a thought or feeling are mechanisms to develop abstract reasoning.
Reason #5. Attitude.
When a problem arises, the attitude that one shows against the possible solution is vital to find a response. The taste for Mathematical problems arises from positive experiences, on the contrary, a bad experience can induce a negative response to the search for solutions. This is one of the most important reasons, not only in the Mathematics area but in all areas of life.
With great sorrow I have heard anecdotes from students, whose parents and teachers, at some point, have told them that they do not have enough capacity for this type of problem. This type of comment lowers the self-esteem of the person.
Be honest with yourself and ask yourself what is the attitude you have to a mathematical problem. Go ahead, know yourself.
Reason #6. Comprhensive reading.
It is always necessary to carefully read the proposed problem, detect words that lead to a certain action, highlight words that are unknown, intuit the main idea, deduce that other ideas are associated. Generally people who have difficulty with mathematics have an apprehensive attitude and tend not to read carefully.
Look for a Mathematical problem, read it and underline all those words or ideas that are unknown to you. How many did you find?
From this simple procedure you will be able to investigate the subject. Empower yourself of the problem.
Reason #7. Background Knowledge
Prior knowledge will always be necessary before trying to address a new topic. A student with serious deficiencies in Mathematics is like a man trying to climb a mountain with a heavy weight on his back. At this point you have to seriously evaluate both the faculty and the education system.
It is always advisable that, insofar as it is read carefully, it is important to highlight the previous knowledge necessary to solve the problem.
For example, suppose you are asked to find the coordinates of a square inscribed in a circle with center at a given point and whose sides are parallel to the coordinate axes.
The following concepts appear in the reading process:
a) coordintates
b) square inscribed
c) Circle with a given center
d) parallelism property
e) coordinate axis
If you succeed in clarifying these preliminary concepts then you will be closer to the desired solution.
Final comments.
In this article I have put some thoughts, one by Albert Einstein and another by Paolo Coelho. Referring to the first one we can conclude that there will always be some difficulty in understanding some mathematical problem, especially when it is new, but knowing the trajectory of productive scientific life and its thinking we can notice a victorious goal.
With respect to Coelho's thought, the following teaching can be obtained: whenever we find a difficulty in the solution of a mathematical problem, let's try to turn it into a challenge, take a lesson out of it and then turn it into a positive attitude for life.


In order not to make the article very long I have only listed some reasons why there is difficulty in understanding Mathematics. Next time I will continue developing this topic taking into account the comments that you as a reader interested in the topic should do well.
Thanks for your attention.
When I teach basic algebra, I try to introduce it as a language; it has to be done slowly or one loses a large part of the class!
Also, algebra is introduced to solve problems that don't require it! For example, x+5=9 can easily be done by most students, yet they are then taught what seems like a complicated method and become befuddled!
That's right. The teaching of Mathematics involves the learning of a new language. This has to be done slowly and with great motivation.
Thanks for your reply.
It is a pleasure to meet you. I will follow you
Congratulations @jorgehh! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP