Actually I meet many scientific misconceptions in my everyday life and communication, but there's one of them that is special for me as for mathematician.
First I want to say, that I do not blame people for it, cause this misconception are cultivated in our minds from school times. Besides, this is rather subtle and doesn't influence much on our life.
It's actually one fundamental misunderstanding of Universe geometry. Are you ready?
In the first formulation it sounds like this:
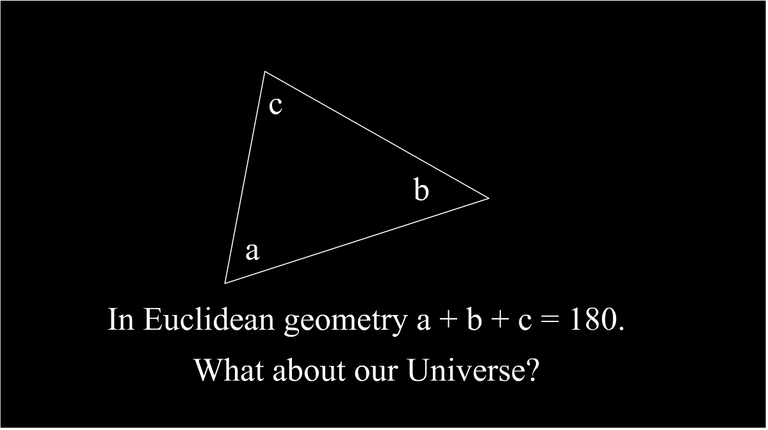
The sum of angles in triangle should be definetely and precisely 180 degrees in physical space.
Is that a misconception? Yes!
The words definetely and precisely are a misconception here. Unfortunately, for our Universe it hasn't been proven!
The only thing we know from experiments, that sum of angles are somewhere between 179.9999... and 180.0000... degrees. It's very close to 180, but there's no proof that it is exactly 180 degrees.
As I've said at the beginning of my post that uncertainty doesn't really influece our everyday life. Despite I'm mathematician I'm not thinking about sum of angles in triangle when I go to the shop for vegetables.

Let's be more serious! Now we are ready to reformulate this misconception and deconstruct it.
In other words, some people just don't understand that Euclidean (Classic) geometry is a model.
Very intuitive and close, but it's still model. This is the appeal of such a delusion. It's very easy to believe in it.
Let's make our post educational now and go deeper in this direction.
The classic geometry have its own history and if you ask your teacher about origins, you'd probably get a reply:
"Well, all this started from axioms". What is actually axioms?
It is statements that are fundamental for theory and have no proof.
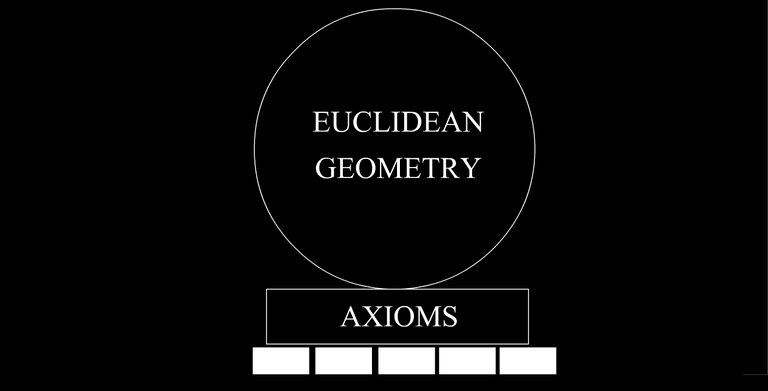
Long time ago Euclid construct his geometry on five such statements (original version):
- "One can draw a straight line from any point to any point."
- "One can produce a finite straight line continuously in a straight line."
- "One can describe a circle with any centre and distance."
- "That all right angles are equal to one another."
- The parallel postulate: "That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles."
This fifth postulate sounds more complicated than other four, doesn't it? So after Euclid many mathematicians tried to make it a theorem - to derive it from the first four statements. Their attemps failed and it quickly becomes clear that parallel postulate is axiom indeed. Actually that means, that it decribe some fundamental property of space and not so obvious.
Things got more interesting when scientists made an attempts to construct a geometry where fifth axioum isn't included.
So Lobachevski and Riemann geometries were invented.
And it turns out, that sum of angles in triangle is not necessary 180 degrees in constructed geometries.
The main question that thinking human can ask now and when - what is true geometry of our Universe?
In modern science, it is considered to depend from so called curvature of the Universe space. The latter is defined by some physical constant - the critical density. Futher explanations will probably lead us far away from the main topic :-)
Note, that there's three possible cases:
- opened space with negative curvature (the sum of angles < 180)
- opened flat space (Euclidean case)
- closed space with positive curvature
Of course, the triangles on which the geometric properties of the universe space manifest themselves must be very large.
Image source: http://wallgallery.org
Now I hope my article make this misconception clear for you.
Share you opinion in comments :-)