Just several hours ago lead developer and founder of the Tauchain project Ohad Asor released his most significant code update yet. This blog post will be to discuss some of those updates and put it into context. In order to make sense of the current codebase : "Tauchain Codebase" I will also discuss a bit about the makeup of the code.
The significant breakthrough - Ohad implements the BDD
First some might be wondering what is BDD? BDD is a data structure called binary decision diagram. This data structure in my opinion is as significant to Tauchain as the "blockchain" data structure was to Bitcoin. For those who do not have a computer science degree I will elaborate on what exactly a data structure is below before discussing what a BDD is and why it is so significant.
Brief discussion on what a data structure is
In programming a data structure is a concept which represents a data organization method. For example blockchain is all about how records are stored as blocks. There are other similar data structures which represent decentralized data management and storage such as for instance the distributed hash table data structure.
A blockchain data structure looks like this for visualization:
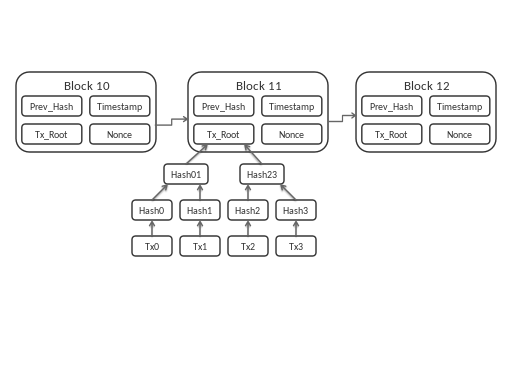
By Matthäus Wander [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], from Wikimedia Commons
A hash table looks like this for a visual:
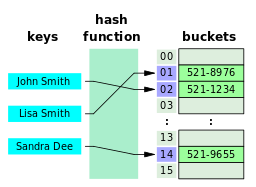
By Jorge Stolfi [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0) or GFDL (http://www.gnu.org/copyleft/fdl.html)], from Wikimedia Commons
The really good programmers choose the appropriate data structure to meet the requirements of the project. BDD was chosen specifically by Ohad because it provides efficiency boosts in a key area necessary for Tauchain to function as intended. In specific we know Tauchain requires partial fixed point logic in order to have decidability in P-SPACE. We also know Tauchain requires decentralization and efficiency. Efficiency can be understood better in terms of the trade off between time and space. We do not have unlimited time or space so we must sacrifice one in order to get more of the other.
Example:
- Compression saves space but increases processing time (this is also related to encryption which costs in processing time).
- A lookup table saves time but costs space.
When we look at the code base we know that Ohad can optimize the code either by sacrificing space in which the executable will be bigger (but the code runs faster) or he can choose to sacrifice time in which the code is a smaller executable to save memory but might run slightly slower. This highlights the essential trade off between time and space when optimizing code but of course there is more to it because algorithms within a code base have to make similar trade offs.
Now what exactly is a BDD (binary decision diagram)?
Now that we understand the basics about efficiency and what a data structure is we can make a bit more sense of what a BDD is. In order to understand why BDD as a data structure is so important to Tauchain we have to remember that Tauchain is about logic. We can take the most basic example of Socrates:
A predicate takes an entity or entities in the domain of discourse as input while outputs are either True or False. Consider the two sentences "Socrates is a philosopher" and "Plato is a philosopher". In propositional logic, these sentences are viewed as being unrelated and might be denoted, for example, by variables such as p and q. The predicate "is a philosopher" occurs in both sentences, which have a common structure of "a is a philosopher". The variable a is instantiated as "Socrates" in the first sentence and is instantiated as "Plato" in the second sentence. While first-order logic allows for the use of predicates, such as "is a philosopher" in this example, propositional logic does not.[5]
Based on the rules of first order logic we can have our inputs and receive our outputs. In the most basic example above we an see a bit about how logic works. To elaborate further:
Relationships between predicates can be stated using logical connectives. Consider, for example, the first-order formula "if a is a philosopher, then a is a scholar". This formula is a conditional statement with "a is a philosopher" as its hypothesis and "a is a scholar" as its conclusion. The truth of this formula depends on which object is denoted by a, and on the interpretations of the predicates "is a philosopher" and "is a scholar".
A truth table has one column for each input variable (for example, P and Q), and one final column showing all of the possible results of the logical operation that the table represents (for example, P XOR Q). Each row of the truth table contains one possible configuration of the input variables (for instance, P=true Q=false), and the result of the operation for those values. See the examples below for further clarification. Ludwig Wittgenstein is often credited with inventing the truth table in his Tractatus Logico-Philosophicus,[1] though it appeared at least a year earlier in a paper on propositional logic by Emil Leon Post.[2]
When we are dealing with logic we may find that a truth table helps with visualization.
Now with this knowledge we have the most basic Socrates example:
- All men are mortal.
- Socrates is a man.
- Socrates must be mortal.
This can be represented via truth table and is called a syllogism. To solve this we simply apply a kind of reasoning called deductive reasoning. This would indicate that if All men are mortal is true and if Socrates is a man is also true then Socrates is a mortal must be true. If we were to say all men are mortal but Socrates is immortal then Socrates cannot be a man. So if Socrates is a man he must be moral or there is what we call a contradiction. Logic is all about avoiding these sorts of contradictions and in specific binary or boolean logic is to reach a conclusion which always must be one of two possible values.
If I ask you to play a game which we want to guarantee will end with either one of two possible outcomes then we have a good example of a boolean function. 1 or 0, true or false, on or off, a or b.
Some of you may be familiar with data structure we call a DAG (directed ayclic graph). For those of you who understand this concept you can visualize a BDD as being very similar to a propositional DAG.
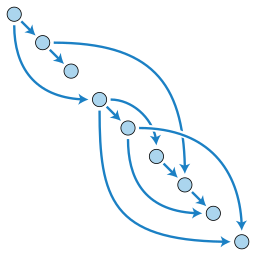
By David Eppstein [CC0], from Wikimedia Commons
We know from DAGs that it's a finite amount of vertices, edges, etc. We may also be able to visualize topological ordering and if you remember my post on transitive closure you might also remember the visuals on how that can work:
A: 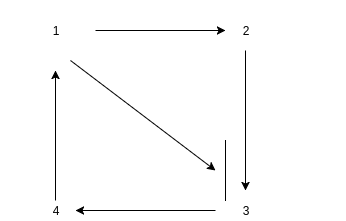
B: 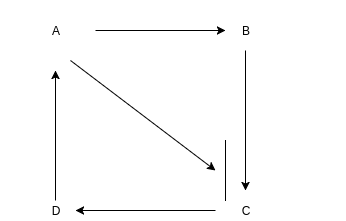
A binary decision diagram can represent a truth table:
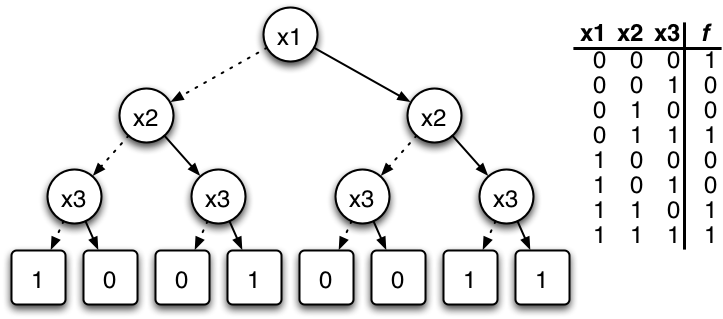
By The original uploader was IMeowbot at English Wikipedia. (Transferred from en.wikipedia to Commons.) [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/)], via Wikimedia Commons
And from these visuals now it should be abundantly clear how this is critical to the functioning of Tauchain. The BDD data structure allows for efficient model checking as well. To understand we have to consider the boolean satisfiability problem.
This highlights the fact that BDD can be used to create a SAT solver.
For example:
A DPLL SAT solver employs a systematic backtracking search procedure to explore the (exponentially sized) space of variable assignments looking for satisfying assignments. The basic search procedure was proposed in two seminal papers in the early 1960s (see references below) and is now commonly referred to as the Davis–Putnam–Logemann–Loveland algorithm ("DPLL" or "DLL").[18][19] Theoretically, exponential lower bounds have been proved for the DPLL family of algorithms.
Without getting overwhelmed by technical details the key points are below:
- BDD is a data structure of immense importance to the Tauchain project.
- BDD enables Tauchain to "come alive" by allowing for even the basic truth table to be applied or the SAT solver to be implemented.
- BDD + PFP is what we see in the Github code base. We see that Ohad has implemented BDD for PFP (binary decision diagram for partial fixed point logic).
To read the code for yourself and track the progress of Tauchain development take a look at Github:
https://github.com/IDNI/tau
https://github.com/IDNI/tau/blob/master/pfp.cpp
I was reading about TML and wondering what are the plans for verification. Curious and it will be helpful if you can share your thoughts.
If you mean formal verification this is covered by the "model checking" capacity of BDD.
References
By formal verification I meant "program verification"
Quoting the paper below, "the runtime safety and the functional correctnes"
https://www.cs.umd.edu/~aseem/solidetherplas.pdf
Right, that will be a result of BDD as I said in my response. Model checking performs formal verification in a process outlined below which I will discuss:
So what we have to understand is every program or software can be thought of as a state machine. There can be said that there are software which has a finite amount of possible states (iterations/combinations/permutations) or an infinite (unknown amount or uncountable is more likely) of possible states. If we are dealing with software which has a finite amount of possible states then it becomes possible to verify that program by simply doing an exhaustive search of the entire map of possible states the program can take in the design. Think of it like the ability to simply play through all possible levels in a game in all possible ways during the design of the game so that when the code is created it's impossible to violate the hard rules such as the laws of physics.
So the answer is yes you get formal verification as an aspect of model checking in Tauchain. In specific the BDD data structure allows for efficient model checking.
https://www.cs.cmu.edu/~aldrich/courses/654-sp05/handouts/model-checking-3.pdf
https://en.wikipedia.org/wiki/Finite-state_machine
http://wiki.c2.com/?InfiniteStateMachine
Thank you - I will revert after having bit more understanding.
Thanks, great explanation. I think BDD's simplicity will come with more surprises.. i dunno, have you watched this? Not sure if related at all but it sure made me think.
This too is interesting:
Sensarma, D., Banerjee, S., Basuli, K., Naskar, S., & Sarma, S. S. (2012). On an optimization technique using Binary Decision Diagram. arXiv preprint arXiv:1203.2505.
https://arxiv.org/pdf/1203.2505.pdf
All their tokens were pre sold, can we buy the tokens now ?
Yes you can. You can find AGRS on either the Bitshares exchange if you're in the USA or if you're in an acceptable country you can use the foreign exchange. Why isn't it on more US exchanges? I'm asking the same question but I suppose until it's more decentralized it will be where it is.
Why isn't it on Coinmarketcap? The only answer I have for that one is politics. It should be on Coinmarketcap at this point.
I would say this though, do not buy the token at the current stage if you think it's some kind of investment. It's right now in the very early stages and not yet decentralized. You're taking a risk and unless you really believe in supporting what the project is about it is not recommended that you put in more than you can afford to lose. I speak for myself, I'm definitely in. I believe in the potential of the technology. I've been in since before anyone knew where the technology would go and have decided to consider it a moon shot project where I'll stay in and see where it leads. I see it similar to Bitcoin 2008 or Ethereum 2015. It could end up being the next great crypto project on technology alone but it's also very ambitious so we have to simply put our money into it on faith at this point and this includes faith in our own ability to understand what is being worked on.
I try to elucidate in my posts what is being worked on to help people understand what I understand.