How did I learn Machine Learning : part 3 - Implement a simple neural network from scratch II

Hi,

In my previous post, I have discussed how does a simple neural network work and what are the notations we are going to use in this series of blogs. Today I am going to present to you how do we implement a simple neural network from scratch. I expect that you have a basic understanding of calculus as we are going to work with some mathematical equations. If you don't have such knowledge, please keep on reading and trying out the examples. I guarantee that you will become an expert in machine learning after the end of this series of blogs. I am trying to explain all the questions as much as simple. Also, I am not going to use any programming frameworks (such as TensorFlow, Keras, etc.) because I need to explain to you how to implement the machine learning stuff without using those programming frameworks. Then you can deeply understand how these things are working. If you do not understand any notation, derivation or expression please refer to the previous blog or put some comment. Let's start ...

In this neural network, we are trying to recognize cats vs. non-cats. For that, we are given a training dataset of 209 images and a test dataset of 50 images. The size of one image is 64*64 pixels, and since those images are colored images there are three channels. We are feeding images one by one to the neural network. There are several ways of feeding an image to a neural network. In this example, a flattened image is fed to the neural network and as a result of that, the number of neurons in the input layer equals 12288 (64pixels * 64pixels * 3channels).

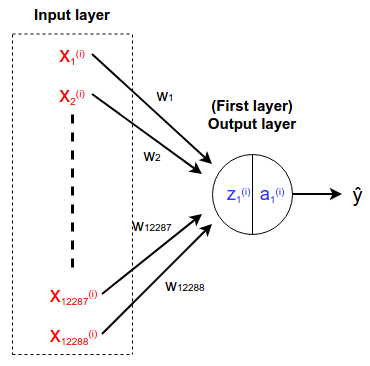
In this network, we don't have any hidden layer and the output layer is the first and only layer. In the output layer, we expect a value between 0 and 1. If that value is greater than 0.5, it is considered as a cat. Therefore we have only one neuron in the output layer. Please refer to the attached image to get an idea about the network architecture.

When we consider the implementation of the neural network, we need to write equations for the forward propagation, cost, backward propagation and updating weights and bias. Forward propagation equations are mentioned below.

eqn (1) : z₁⁽ⁱ⁾ = w₁x₁⁽ⁱ⁾ + w₂x₂⁽ⁱ⁾ + ... + w₁₂₂₈₈x₁₂₂₈₈⁽ⁱ⁾ + b
eqn (2) : ŷ⁽ⁱ⁾ = a₁⁽ⁱ⁾ = g(z₁⁽ⁱ⁾)

Now we should calculate the cost per data(L) and cost for the whole dataset(J).

eqn (3) : L(a₁⁽ⁱ⁾, y⁽ⁱ⁾)⁽ⁱ⁾ = -y⁽ⁱ⁾log(a₁⁽ⁱ⁾) - (1 - y⁽ⁱ⁾)log(1 - a₁⁽ⁱ⁾)
eqn (4) : J = (Σ_i=1^mL(a₁⁽ⁱ⁾, y⁽ⁱ⁾)⁽ⁱ⁾)/m

Now we should calculate the derivative for each weight and bias(∂J/∂w₁, ∂J/∂w₂, ∂J/∂b₂, ... ) such that the cost should be reduced in each iteration. Let's try to calculate the ∂J/∂w₁ and I will write ∂J/∂w₁ as ∂w₁. By the chain rule we can calculate the ∂w₁ as follows.

eqn (5.1) : ∂w₁ = ∂J/∂w₁ = (Σ_i=1^m∂L⁽ⁱ⁾/∂w₁)/m
eqn (5.2) : ∂L⁽ⁱ⁾/∂w₁ = ∂L⁽ⁱ⁾/∂a₁⁽ⁱ⁾*∂a₁⁽ⁱ⁾/∂w₁
eqn (5.3) : ∂a₁⁽ⁱ⁾/∂w₁ = ∂a⁽ⁱ⁾/∂z₁⁽ⁱ⁾*∂z₁⁽ⁱ⁾/∂w₁

Using eqn (5.2) and eqn (5.3),
eqn (5.4) : ∂L⁽ⁱ⁾/∂w₁ = ∂L⁽ⁱ⁾/∂a₁⁽ⁱ⁾*∂a⁽ⁱ⁾/∂z₁⁽ⁱ⁾*∂z₁⁽ⁱ⁾/∂w₁

By getting the derivative of the eqn (3) w.r.t. ∂a₁⁽ⁱ⁾,
eqn (5.5) : ∂L⁽ⁱ⁾/∂a₁⁽ⁱ⁾ = - y⁽ⁱ⁾/a₁⁽ⁱ⁾ + (1-y⁽ⁱ⁾)/(1-a₁⁽ⁱ⁾)

Let's assume activation function g() is sigmoid function. Therefore ∂a⁽ⁱ⁾/∂z₁⁽ⁱ⁾ equals the derivative of sigmoid function.
eqn (5.6) : ∂a⁽ⁱ⁾/∂z₁⁽ⁱ⁾ = a₁⁽ⁱ⁾(1 - a₁⁽ⁱ⁾)

By getting the derivative of the eqn (1) w.r.t. dw₁,
eqn (5.7) : ∂z₁⁽ⁱ⁾/∂w₁ = x₁⁽ⁱ⁾

By substituting eqn (5.5), eqn (5.6) and eqn (5.7) into eqn (5.4) and simplifying the expression,
eqn (5.8) : ∂L⁽ⁱ⁾/∂w₁ = (a₁⁽ⁱ⁾ - y⁽ⁱ⁾)x₁⁽ⁱ⁾

By substituting eqn (5.8) into eqn (5.1),
eqn (6) : ∂w₁ = (Σ_i=1^m(a₁⁽ⁱ⁾ - y⁽ⁱ⁾)x₁⁽ⁱ⁾)/m

Following the eqn (6), we can write derivate for all weights.

∂w₂ = (Σ_i=1^m(a₁⁽ⁱ⁾ - y⁽ⁱ⁾)x₂⁽ⁱ⁾)/m ...
∂w₁₂₂₈₈ = (Σ_i=1^m(a₁⁽ⁱ⁾ - y⁽ⁱ⁾)x₁₂₂₈₈⁽ⁱ⁾)/m

Since ∂z₁⁽ⁱ⁾/∂b = 1,
eqn (7) : ∂b = ∂J/∂b = (Σ_i=1^m(a₁⁽ⁱ⁾ - y⁽ⁱ⁾))/m

Now we have to update the weights and bias as shown below.

eqn (8) : w₁ = w₁ - α*∂w₁ ...
w₁₂₂₈₈ = w₁₂₂₈₈ - α*∂w₁₂₂₈₈
eqn (9) : b = b - α*∂b

Finally, we have derived all the questions we need to implement our neural network. In the next blog post, I will explain to you how to implement our neural network using theses equations. Please feel free to raise any concerns/suggestions on this blog post. Let's meet in the next post.

Sort:

Trending

[-]

steemitboard (66) 5 years ago

Congratulations @boostyslf! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :

	You published more than 10 posts. Your next target is to reach 20 posts.
	You got more than 10 replies. Your next target is to reach 50 replies.

_{You can view your badges on your Steem Board and compare to others on the Steem Ranking}
_{If you no longer want to receive notifications, reply to this comment with the word STOP}

To support your work, I also upvoted your post!

Vote for @Steemitboard as a witness to get one more award and increased upvotes!

$0.00