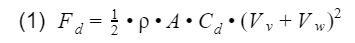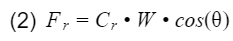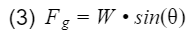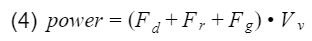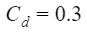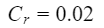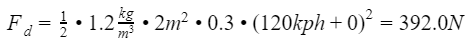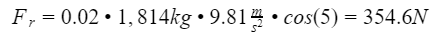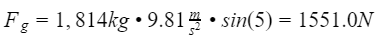Hello Steemit friends.
Have you ever wonder how much power a vehicle needs to go down the road? In this post, I will go through and calculate the road load, and the power to overcome it.
Road load: The force acting on a vehicle as it travels down the road.
https://www.pexels.com/search/car/
Let's think about what forces make up the road load. As we drive, there will be drag force from the air, friction between the tires and the road, and if we are on a hill, there will also be gravity pulling the vehicle down. These three forces make up the road load, and govern how much power a vehicle need to maintain a certain speed.
Let's now dive into the math. The drag force cause by air is call aerodynamic drag, and can be calculated by
where p is the density of air, A is the front cross sectional area of the vehicle, Cd is the drag coefficient, Vv is the speed of the vehicle, and Vw is the speed of the wind(in the direction towards the vehicle). As you can see, the sum of the speeds have a power of 2. That means as you increase vehicle speed, the aerodynamic drag will increase significantly. Next, we have the frictional force between the tires and the road. This force is referred to as rolling resistance, and is calculated by
where Cr is the rolling resistance coefficient which account for tires and road characteristics, W is the weight of the vehicle(including driver and all passengers), and theta is the angle of the hill. If you are not on a hill, theta is 0, and the cosine of 0 is 1. Finally, we have the gravity force. Similar to the rolling resistance, the gravity force is proportional to the vehicle’s weight and the angle of the hill, and can be calculated by
If there is no hill, sine(0) is 0, and the gravity force acting on the vehicle will be 0. Take a moment to conceptually think about these forces and visualize them. Understanding what these three forces are is the hard part. To find the power require, we add these three forces together, and multiply by the speed.
Now that we know all the forces a vehicle must overcome, lets plug in some numbers. Say your vehicle is 4,000lbs(1,814kg) traveling at 75mph(120kph or 33m/s) with no head wind, up a 5 degree hill, and has a frontal area of 2m^2. Notice our formulas use weight, and not mass. If we calculate using mass(kg), we will need to multiply by gravitational acceleration which is 9.81m/s^2. For the air density, drag coefficient, and rolling resistance coefficient, I will use values from www.engineeringtoolbox.com assuming an ambient temperature of 20 degree celsius.
Using the above values, lets calculate the forces.
Now we calculate power.
The calculation tell us that the vehicle needs 101hp to maintain 120kph up a 5 degree slope. If the vehicle does not have 101hp, it will start to slow down. If the vehicle is to accelerate above 120kph, it will need to make more than 101hp.
As a quick recap, we learned there are three forces that act on a vehicle as it goes down the road - aerodynamic drag, rolling resistance, and gravity(if we are on a hill). When we sum these three forces together, and multiply by the vehicle speed, we get the total power needed to maintain that speed. Keep in mind that due to engine and drivetrain efficiencies, the engine will make more hp than what we calculated for road load. If you haven’t already, check out my previous post on engine efficiency called The Simple Math Behind Engine Efficiency.
Thanks for stopping by, and have a great day.
The superior man is modest in his speech, but exceeds in his actions. -Confucius