Background
In Machine Learning there are several models but Neural Networks have become very popular recently. Neural Networks have a been around for a while but only recently have they been excelling. This is attributed to the advancements in computer hardware (GPU for parallel computation) and big data (more data to learn and generalize from). They've helped produce some amazing breakthroughs in image recognition, natural language processing, speech recognition and its only the beginning.
The Perceptron
The perceptron is one of many linear classifiers which makes predictions based on a linear function combining a set of weights (feature extractors) with the input vector.
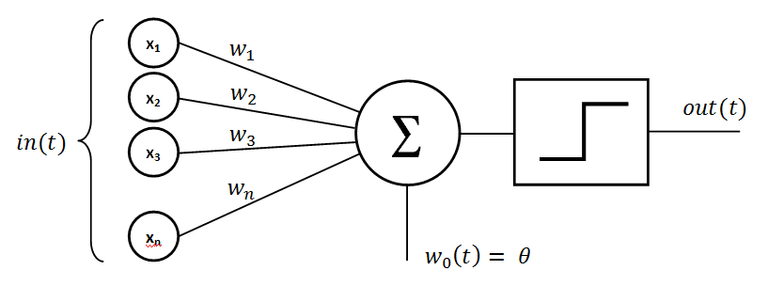
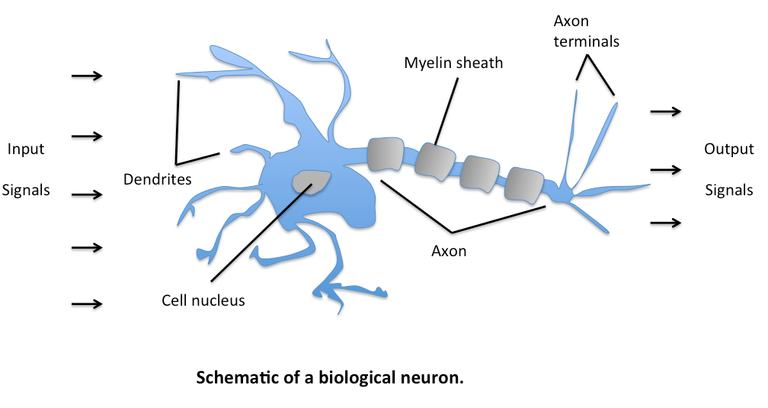
The Perceptrons motivation came from a neuron in the brain. It can be perceived as a cell which receives an input and outputs a signal. By continuously increasing or decreasing the weights depending on what the Perceptrons output was after each training example or a set of training examples the predictions become more accurate.
The MLP
As mentioned the Perceptron is a linear classifier which means it is a method which will only be able to perform well on linearaly separable data. That is why the multilayer Perceptron (MLP) wasy introduced. Its multiple layers and non-linear activation distinguish MLP from a linear Perceptron.
In the MLP the first layer is the input layer. Each node in this layer takes an input, and then passes its output forward along the network as the input to each node in the next layer. Having many hidden layers in an Artificial Neural Network is what makes these networks Deep and capable of learning higher order features. The MLP utilizes a supervised learning technique called backpropagation for training.
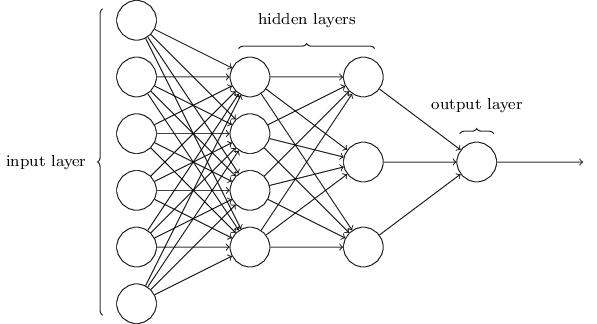
Deep Learning in essence is an extension of the Perceptron. If the Perceptron was a single neuron then Neural Networks are inspired by the structure of the cerebral cortex.
Code
Here is an example of an implementation of an MLP using the numpy python library to learn the xor function. In future posts we will use libraries which provide the Neural Network implementation for us.
Happy AI blogging!!
Make sure to up vote if you enjoyed.
From neurallearner :)
import numpy as np
import time
n_hidden = 10
n_in = 10
n_out = 10
n_samples = 300
learning_rate = 0.01
momentum = 0.9
np.random.seed(0)
def sigmoid(x):
return 1.0/(1.0 + np.exp(-x))
def tanh_prime(x):
return 1 - np.tanh(x)**2
def train(x, t, V, W, bv, bw):
# forward
A = np.dot(x, V) + bv
Z = np.tanh(A)
B = np.dot(Z, W) + bw
Y = sigmoid(B)
# backward
Ew = Y - t
Ev = tanh_prime(A) * np.dot(W, Ew)
dW = np.outer(Z, Ew)
dV = np.outer(x, Ev)
loss = -np.mean ( t * np.log(Y) + (1 - t) * np.log(1 - Y) )
# Note that we use error for each layer as a gradient
# for biases
return loss, (dV, dW, Ev, Ew)
def predict(x, V, W, bv, bw):
A = np.dot(x, V) + bv
B = np.dot(np.tanh(A), W) + bw
return (sigmoid(B) > 0.5).astype(int)
# Setup initial parameters
# Note that initialization is cruxial for first-order methods!
V = np.random.normal(scale=0.1, size=(n_in, n_hidden))
W = np.random.normal(scale=0.1, size=(n_hidden, n_out))
bv = np.zeros(n_hidden)
bw = np.zeros(n_out)
params = [V,W,bv,bw]
# Generate some data
X = np.random.binomial(1, 0.5, (n_samples, n_in))
T = X ^ 1
# Train
for epoch in range(100):
err = []
upd = [0]*len(params)
t0 = time.clock()
for i in range(X.shape[0]):
loss, grad = train(X[i], T[i], *params)
for j in range(len(params)):
params[j] -= upd[j]
for j in range(len(params)):
upd[j] = learning_rate * grad[j] + momentum * upd[j]
err.append( loss )
print "Epoch: %d, Loss: %.8f, Time: %.4fs" % (
epoch, np.mean( err ), time.clock()-t0 )
# Try to predict something
x = np.random.binomial(1, 0.5, n_in)
print "XOR prediction:"
print x
print predict(x, *params)
This is really interesting. Do you mind commenting the code a little bit more so I can see where the hidden layers are?
You got it!! Thanks for the recommendation :)
This is old school neural network 101 stuff....like dating back >30 years.
Would have upvoted @neurallearnermore more if you put in lots of references.
Don't worry we will get to the more advanced topics 😉 (i.e. attention models, capsule networks ect.) we are open to suggestions though.