NB: This article was co-written by @balzss and is part of a series we are creating together. Half of them will be released on his blog so make sure to follow him if you find this interesting.
The time when we only put the Turing-complete label on efficient and productive programming languages has long gone and "esolang" as a genre has grown to be a common phenomenon. Esolangs are programming languages usually with the sole purpose of not being useful. They are sophisticated in-jokes for programmers usually satirizing actual languages.
But what does Turing-complete mean anyway? It means that it can calculate anything computable. That's not a satisfactory answer so let's put it this way: something is Turing-complete if it can calculate anything that a Universal Turing Machine can (it turns out there is no way to go beyond that currently).
So Turing-completeness is something that programming languages (real and esoteric) are aiming for but that doesn't mean they are some privileged creature and the only canidate for the title. If you look carefully enough you'll find it everywhere you wouldn't have expected and in this article we want to list 6 that we found the most interesting.
1. Manufactoria

Manufactoria is a game about putting robots in their place. More accurately it's a visual programming environment where you accept or reject robots based on the content of their tapes. You also need to transform their input to a valid output on some levels.
The basic building blocks are branches to send robots to alternative directions based on the read bit, conveyors which send a robot to a pre-defined cell, and writers that add a new color-bit to the end of the tape. Starting with simple mazes the player learns how to create more and more intricate circuits. Beware! The learning curve is quite steep.
It's not surprising that this game is Turing-complete. It is proven by this Rule 110 interpreter which is itself Turing-complete. Nevertheless, it's a great place to start learning about Turing Machines and a good way to exercise the mind.
2. Jonathan Blow's Platformer Classic: Braid


First of all: if you haven't played the game, you seriously should. This is one of my all-time favorites and I was blown away when I learned that the game is not just beautifully designed with a fascinating storyline but also Turing-complete. To be fair, the game isn't Turing-complete as it is but rather the game mechanics. Linus Hamilton in his 2014 whitepaper, Braid is undecidable walks us through the specific game elements we need to prove Turing-completeness. These elements are:
- monstars
- bunnies
- rewinding time
- lever+platform
- one-way surfaces
- cannons
He shows how to create a counter machine out of these elements which are:
one of the simplest types of machines known to exhibit Turing-complete behavior.
The machine is fairly complex but he provides images and explanation for every part so it's not so difficult to follow along. Later he also proves that Braid is undecidable but that's not the scope of this article. If you want to know all the details I highly recommend reading the whole paper.
3. Minesweeper
Originally I was going to include Game of Life here. It's true that the final goal of Conway's game wasn't creating a Turing-complete system but something organic, chaotic and therefore life-like (hence the name). But it's still a product of computation research so not unintentional enough for this article.
Then I came across a paper by Richard Kaye about Minesweeper. He compares its grid-like nature and the values contained by each cell to Game of Life and proposes that Minesweeper is Turing-complete as well.
The paper goes into very fine details but the essence of the concept is handling an initial state (when some tiles are visible and some not) as an instruction set for a Turing Machine and the "extension" of that grid (when every tile is visible) as the result of the computation. The actual proof is a bit hard to grasp but if you are not afraid of maths then give the paper a try!
4. Music Notation
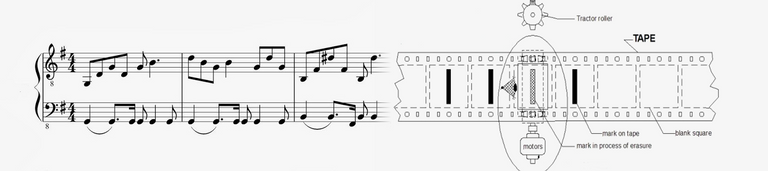
Who thought that even music can represent arbitrary computations? Well, if you made it this far you probably don't get too excited anymore (I'm sorry, I guess...). But how crazy is that? The standard notation musicians use today is more than 300 years old which predates Turing by a fair bit. Utilizing it is not as straightforward though and requires some clever solutions.
In 2002 Stephen Sykes released his esoteric programming language/interpreter Choon which needs standard music notation as an input and outputs real music in the form of a .wav file. I think the most interesting thing about it is that it doesn't use alterable storage as opposed to common programming languages. Unfortunately, his original article is not available anymore and you need the Wayback Machine to access it but it sure worth a read.
5. PowerPoint
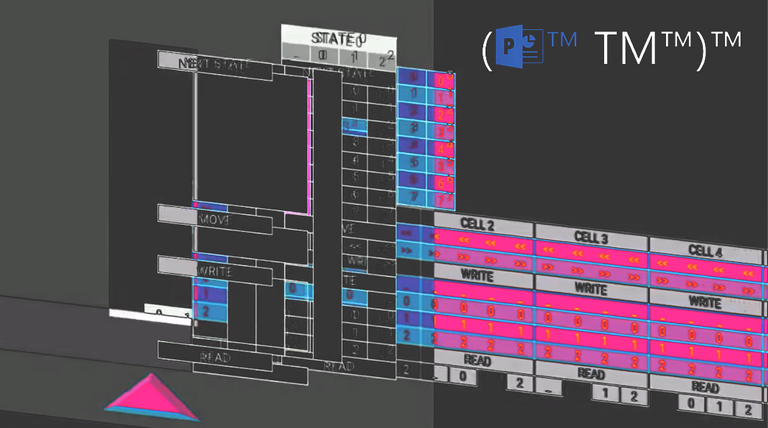
(PowerPoint™ Turing Machine™)™ is the realization of a joke that got too far. First presented at SIGBOVIK, the flagship conference of the Association for Computational Heresy, Tom Wildenhain manages to turn a PowerPoint slide into a classical Turing Machine with the usage of AutoShapes, Hyperlinks and On-Click Animations.
The unique animation support made it possible to create this machine, but the user needs to click multiple times to advance the computation, but this limitation makes it even more amusing. Cookie Clicker skills translate to a faster CPU! Programs are created by manually editing the punch cards with the builtin PP tools.
If you're interested in more technical details, check out the whitepaper (typeset in PowerPoint) or download the machine itself.
6. Rail Transportation

Train transportation and the infrastructure around it comes at a humongous price so it's quite understandable why we've yet to witness a Turing-complete train system implementation in real life. But that doesn't mean such a thing couldn't be done and to prove it we just need a simulation platform that offers realistic building blocks and behavior that works the same as real trains. The best tool for this is OpenTTD and open source tycoon game where you can build and manage transportation systems but we obviously don't need the whole game just the trains in it.
The first building block is a binary full adder implemented in the game by Alienturnedhuman (the name seems accurate) who demonstrated his creation in a youtube video in early 2015. Not a full year after he released a 45 minute long update video in which he expands his full adder with a clock, memory and whole arsenal of "connection circuits" and basically creates a working computer. Well, not so much a working computer because the video shows a work-in-progress state and only outlines the path from there to create a fully working Universal Turing Machine.
Other interesting aspects of Alienturnedhuman's project is the motivation. He explains in the video how he had an argument with one of his friend who praised Minecraft for the fact that you can build functioning computers in it. He replied that you surely can build computers with older games and proved it with this mind-blowing project. Definitely watch the whole video for all the details!