Motivation
After having made an introductory post in my last tutorial, presenting the general theory behind Linked Lists and implementing a Singly Linked List in Go, I want to dive deeper this time. I will be be presenting more types of lists, and I want to kick start the "algorithms" part of my tutorials, by presenting two problems one might expect to encounter when studying Linked List. These are also the type of issues that might be raised during a programming interview. You can skip directly to the code.

What Will I Learn?
By the end of this tutorial, you will be able to :
- Explain what Doubly Linked List are, differences between types of linked lists
- Implement a Doubly Linked List in Go
- Learn to detect a cycle in a Linked List, check to see if a list is a palindrome
Requirements
- Install Go on your machine ( Go)
- Plain text editor, or a more powerful IDE (I use Goland)
- Basic Go syntax knowledge
- Basic understanding of how interfaces work in GO (you can read about that here)
- A desire to learn
Difficulty
- This tutorial has a basic level of difficulty.
Tutorial Contents
I will explain what Doubly Linked Lists are, what Circular Linked Lists are and make some comparisons between them. I will implement a Doubly Linked List and present two algorithms on Linked Lists, one to check if a list is a palindrome and one to detect if there are loops in a linked list.
Workspace Setup
Install Go on your machine. Download the code or code as you read through this article. Alternatively, you can try and implement your on version of a doubly linked list, after having read this tutorial or at least try code the interview questions yourself.
What is a Doubly Linked List?
Just like Singly Linked Lists, Doubly Linked Lists are data structures in which objects are arranged in a liner order. Each node from the list knows about the next one. Unlike the Singly Linked Lists though, the node from a Doubly Linked List knows about the previous node as well. More technically speaking, it also has a pointer to the previous node. Here would be a representation of such a list:
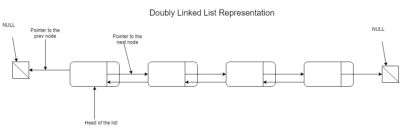
Other types of Linked Lists
A list can have more than the two forms presented. It may be singly linked, doubly linked, it may be sorted, or circular.
A sorted linked list has all nodes in order. For this to happen, the data stored in each node must be comparable. As you can imagine, inserting a new node into such a list would be a more "expensive" operation than usual, as we would need to maintain the nodes sorted.
A circular linked list can be either singly linked or doubly linked. A singly linked circular list has the next pointer for the last node pointing to the first node of the list instead of pointing to null. A doubly linked, circular list has the last node in the list next pointer pointing to the first node, the head. Also, the head's prev pointer points to the last node in the list. Here is a visual representation:
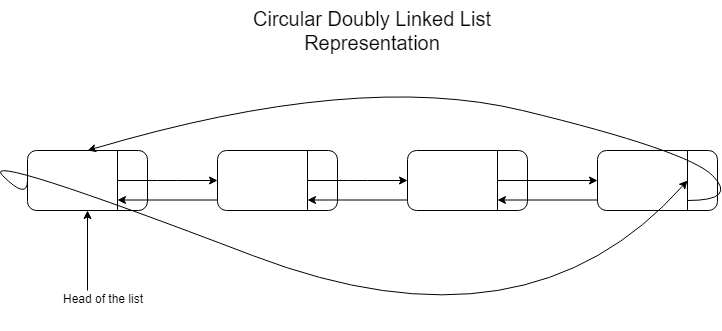
Doubly Linked List Implementation
I have decided to implement the doubly linked list for this tutorial. My linked list struct contains a pointer to the head node and a size. A node, contains a pointer to the next node, a pointer to the previous Node as well the data, which in my case can be any Golang structure. I have decided to implement the most important list operations, i.e, insertion, node deletion, and node searching. There are also some extra operations, for pretty printing the list and checking if the list is empty. I drew lots of inspiration for the implementation from the Cormen book on algorithms, a book I wholeheartedly recommend everyone who is interested in learning the fundamentals of computer science.
type Node struct {
next *Node
prev *Node
data interface{}
}
type DoublyLinkedList struct {
head *Node
size int
}
List methods
We need two basic functionalities for our list, namely to be able to add and remove items. As we keep a pointer to the head of the list, inserting new nodes there is very efficient, as it requires only updating pointers. So, any new nodes, automatically become the head of the list. The next pointer for the new node will point to the old head, and the prev pointer of the old head will point to the new head. Pretty simple, right? Here is the visualization and the code for this add operation:
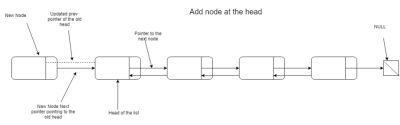
// Insert add a node at the head of the list, a O(1) operation
func (l *DoublyLinkedList) Insert(item interface{}) {
newNode := &Node{data:item}
l.size ++
if l.IsEmpty() {
l.head = newNode
return
}
l.head.prev = newNode
newNode.next = l.head
l.head = newNode
}
Another useful method is list search, which takes the item stored in a node as a parameter and searches for it in the linked list. The worst case time performance of this method is O(n), which means we have to go through all the nodes in the list. We return the node and a boolean flag, true if the node is indeed part of the linked list, or null and false if the node is not part of the list.
// ListSearch performs a scan of the list and returns
// the node with the given key. It has O(n) worst case time
func (l *DoublyLinkedList) ListSearch(item interface{}) (*Node, bool) {
for p := l.head; p != nil ; p = p.next {
if p.data == item {
return p, true
}
}
return nil, false
}
Delete performs the removal of a node from a doubly linked list. This method just updates pointers, so it has constant time complexity. We treat separately the pointer updates if the nodes are either the head node or the last node. If the node we want to remove is the head node, we just update the list head with the next pointer of the old head (l.head = node.next ). If we remove a random node, we update its previous node next pointer to point to the next of the node we want to remove (node.prev.next = node.next). We must also update the prev pointer of the next node to point to the node behind the one we remove : node.next.prev = node.prev. This last operation is not required if the node we remove is the last node in the linked list.
// Delete performs a removal of a node in O(1) time,
// by updating pointers
func (l *DoublyLinkedList) Delete(node *Node) {
// if the node != head
if node.prev != nil {
node.prev.next = node.next
} else {
l.head = node.next
}
// if the node != the last node
if node.next != nil {
node.next.prev = node.prev
}
l.size --
}
Finally, we want a method that takes data stored in a node and remove that node from the list. Unlike the previous delete method, this one requires that we locate the node in the linked list before removing it, meaning we must use our list search method, losing thus the constant time performance. We remove the item, by locating the node with our list search method and then calling the delete method with the located node as parameter. This function has the same time complexity as the list search method. Here is the code:
// RemoveItem remove node with key = item. Runs in O(n) time,
// as it needs to call ListSearch to locate the node
func (l *DoublyLinkedList) RemoveItem(item interface{}) {
node, ok := l.ListSearch(item)
if !ok {
return
}
l.Delete(node)
}
Printing your list, putting everything together
Now that we have implemented this list operations, it is time we test them! We first create a print function, that goes through all the nodes in the list and appends their data to a string. We join the string using an arrow that points in both directions, symbolizing the next and prev pointers:
func (l *DoublyLinkedList) Print() {
p := l.head
str := ""
for p != nil {
str += fmt.Sprintf("%v <---> ", p.data)
p = p.next
}
fmt.Print(str)
}
Now, using the main function, we create a new Doubly Linked List, add some elements, remove some and print the result!
func main() {
list := lists.NewDoublyLinked()
list.Insert(1)
list.Insert(2)
list.Insert(3)
list.Insert(4)
list.Insert(5)
list.RemoveItem(3)
list.RemoveItem(5)
list.Print()
}
Interview algorithms
Now that we have implemented our list, let's try and solve some linked lists interview questions. You can use the linked list implementation from my previous tutorial as well. We will implement an algorithm that checks if the Doubly List is a palindrome and one algorithm that detects loops in a linked list.
Palindrome
A palindrome is simply a sequence of characters which reads the same backward as forward (121, madam). In our case, a character would be the data contained in the node of a linked list. The approach when checking whether a doubly linked is a palindrome would be to have two pointers, one at the head and one at the end of the list, each going in opposing directions and meeting at the middle of the list. Along the way we check for the data in the each opposing nodes to be equal. Here is the code:
func (l *DoublyLinkedList) IsPalindrome() bool {
if l.IsEmpty() {
return true
}
headNode := l.head
lastNode := l.head
// make the last node point to the tail of the list
for lastNode.next != nil {
lastNode = lastNode.next
}
// stoop the loop when the pointers meet at the middle of the
// list
for lastNode != headNode {
if lastNode.data != headNode.data {
return false
}
// one pointer goes in one direction, the other
// goes in the opposite direction
lastNode = lastNode.prev
headNode = headNode.next
}
return true
}
Checking for a palindrome is a bit harder if the list is singly linked, but there is a way to do it with the same complexity!! I will not spoil the surprise, maybe you guys can give me a nice solution in the comments!
Detect a loop in a linked list
For this algorithm it does not matter whether the list is singly linked or doubly linked.
Loops in linked list occur if the list is malformed. A loop occurs if:
- the list has no end (the next pointer of the last node does not point to null)
- the list contains two links to some node
This is how such a list would look like:
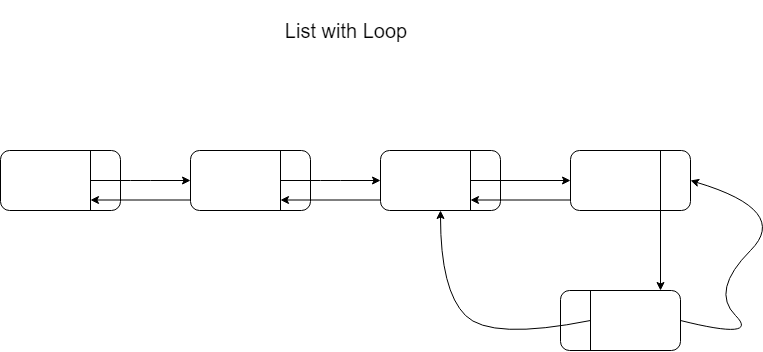
There is more than one method of checking for loops, but the best one I know is the “Floyd’s Cycle-Finding Algorithm”. It sounds fancy, but the idea behind it's simple. We take two pointers, both starting at the head of the list. One pointer moves slowly, i.e. goes from node to node and the other one moves twice as fast. If there is a loop, the fast pointer will lap the slow pointer and they will meet. If this happens, then there is a cycle in our list. This algorithm has O(n) time complexity and requires O(1) extra space. Implementation:
func (l *DoublyLinkedList) HasLoop() bool {
if l.IsEmpty() {
return false
}
slowPointer := l.head
fastPointer := l.head
for slowPointer != nil && fastPointer != nil && fastPointer.next != nil {
slowPointer = slowPointer.next
fastPointer = fastPointer.next.next
if slowPointer == fastPointer {
return true
}
}
return false
}
Conclusion
Thank you if for reading my tutorial. We have learned about Doubly Linked Lists, Circular Lists, Sorted Lists and implemented the Doubly Linked one. We have also applied our implementation to two algorithms. The code for this tutorial can be found here.
Curriculum
I would strongly advice that you read Part 2 of this series, in order to have more context of what's going on.
Learn Algorithms & Data Structures with GO | Part 1 | Stacks and Queues
Learn Algorithms & Data Structures with GO | Part 2 | Singly Linked Lists
References
- Introduction to Algorithms, Cormen, Leirson, Rivest and Stein, Chapter III, Data Structures
- Geeks for Geeks
- Wikipedia Doubly Linked List
Posted on Utopian.io - Rewarding Open Source Contributors
Hey @prometheus21 I am @utopian-io. I have just upvoted you!
Achievements
Community-Driven Witness!
I am the first and only Steem Community-Driven Witness. Participate on Discord. Lets GROW TOGETHER!
Up-vote this comment to grow my power and help Open Source contributions like this one. Want to chat? Join me on Discord https://discord.gg/Pc8HG9x
Thank you for the contribution. It has been approved.
You can contact us on Discord.
[utopian-moderator]
@prometheus21, Like your contribution, upvote.
This post has received a 2.42 % upvote from @speedvoter thanks to: @prometheus21.
Your Post Has Been Featured on @Resteemable!
Feature any Steemit post using resteemit.com!
How It Works:
1. Take Any Steemit URL
2. Erase
https://3. Type
reGet Featured Instantly � Featured Posts are voted every 2.4hrs
Join the Curation Team Here | Vote Resteemable for Witness