Do indications from known math support the Lost Abenmoad story?

Could an overlooked medieval method for spherical projection of regular polyhedra enable modern math experts to win the factorization race and penetrate strong digital encryption?

Chapter 2 of Zigzag Sphere — a serial inquiry

Read this chapter by itself, or with Chapter 1.

about the author

THE 1983 DEATH of Muhammad Idris as-Senussi, Libya’s former king, brought a couple of neighbors together in the UK once they heard the news. One reminisced about attending a “royal lesson” in Benghazi some 30 years before, taught by the king himself, reading aloud and sketching diagrams from the Senussi copy of an extremely rare treatise by ibn Muadh al-Jayyani, the Andalusian spherical trigonometry pioneer, known in medieval Europe as Abenmoad. This neighbor, Arab yet non-Libyan, I’m calling “Lubayd al-Wali as-Satna” — not his actual name. He even reproduced on a chalkboard some of the sketches from his memory of meeting the erudite king. The sketches demonstrated a “zigzag method” for projecting regular polyhedra onto the unit sphere. Thus begins the unverified story of the Lost Abenmoad.

The other neighbor, on whose chalkboard Lubayd sketched, knew enough higher math to realize he was looking at a projection method that, in a modern context, could advance prime number theory, categorize very large composite numbers, accelerate their factorization, and thereby revolutionize cryptography. That neighbor, a Brit, I’m calling “Benedict Benedict” — not his actual name. On the spot, he developed a prime factorization conjecture. Over subsequent months, he assembled a team that made it ready for publication. Then Benedict and other team members were confronted, and threatened with “recruitment or worse,” by covert NATO agencies that had previously developed the same conjecture and had already obtained from it the Cold War advantage of a monopoly on quick digital decryption.

The agents confronted Benedict during early 1984, when he was in the USA near a studio affiliated with National Public Radio. Once the agents left him to consider his options, Benedict went straight there, got himself interviewed, and got his interview broadcast nationwide. In the broadcast, he revealed just barely enough to assure that, if involuntary “recruitment or worse” later curtailed his life or liberty, NATO’s quick digital decryption monopoly, and the prime factorization conjecture they were trying to keep secret, would get precisely the kind of publicity they were trying to avoid.

Because the broadcast involved making an extraordinary claim — of having solved the problem of rapid factorization — without evidence, without even a specific description of his conjecture, it made Benedict a laughingstock among his colleagues, as he knew it would. Yet his tenure, or its Welsh equivalent, assured that he could keep his job. And the broadcast gave American listeners like me a story to track. After the Soviet Union was disbanded and the Cold War ended, Benedict felt secure enough to publish hints to his conjecture in a couple of books.

Eventually, however, the story sank into an astonishing degree of obscurity, the likes of which I have rarely, if ever, seen. Today, Benedict’s conjecture, and the larger Lost Abenmoad story of which it is part, are not mentioned in English anywhere on the web at all, except here in my Busy / Steemit serial inquiry, Zigzag Sphere.

Many details in the Lost Abenmoad story provide reasons to be skeptical. Confirming what, if true, must surely be NATO’s most highly classified secret is quite the challenge, to say the least. Arabic and Urdu speakers have the potential to investigate the purported history of the ibn Muadh document nicknamed the Lost Abenmoad. English speakers, however, have nowhere to go but known math.

Are there indications, amid what is publicly known of mathematics, that Benedict’s claimed conjecture could be true, and a quick way to break strong public key encryption might be real? Let’s look into it.

Platonic dice

There are only five regular convex polyhedra, also called Platonic solids, realized here as dice. In order from left to right, they are the regular tetrahedron, cube, octahedron, dodecahedron, and icosahedron. Unlike the regular polygons, the regular polyhedra are finite in number.

THE NATURAL NUMBERS make a dotted line that, in the decreasing direction, gets no smaller than 1. Yet in the opposite direction — that of increase — it always extends ever farther, shooting its arrowhead straight to infinity. Obviously, for any natural number, you can make or find the next larger number by adding 1 to it.

All the even numbers greater than 2 are composites. All primes greater than 2 are odd numbers. Otherwise, the pattern of the placement of primes along the dotted line remains baffling and elusive. Even just calculating the number of primes that don’t exceed a given magnitude has been a challenge so difficult as to frustrate and obsess humanity’s most brilliant minds.

Aside from putative advances — like Benedict’s conjecture — that might be kept secret from the public, only the Riemann hypothesis has made serious progress in this field. Despite Riemann’s brilliance, his hypothesis has not yielded any known computational shortcuts to the factorization of relatively large composite numbers.

Natural numbers greater than 2 — including all odd primes and all composite numbers — extend into infinity. Correspondingly, the regular polygons, each with a number of sides greater than 2, extend into infinity as well. Obviously, for any regular polygon, you can make or find another by adding 1 to its number of sides.

Both polygons and polyhedra are types of polytope. A regular polytope is a shape with equal corners and equal sides.

A regular polygon is a two-dimensional regular polytope, where the sides are 1D line segments, and the corners are 2D angles.

A regular polyhedron is a three-dimensional regular polytope, where the sides are 2D “faces” or “facets” or polygons, and the corners are 3D “solid angles” or vertices.

Here is a startling and relevant fact. When you increase dimensionality from 2 to 3, the number of regular polytopes drops — from infinity, the number of regular polygons — down to 9, the number of regular polyhedra — or (by some interpretations) even farther down to 5, the number of Platonic solids.

Excluding the prisms and antiprisms, even the uniform polyhedra, though more numerous than the regular polyhedra, are still finite in number.

The drop from infinity to the finite that comes with increasing polytope dimensionality from 2 to 3 is our first indication, suggesting that polyhedral insights might somehow make the infinitude of composite numbers needing factorization more manageable.

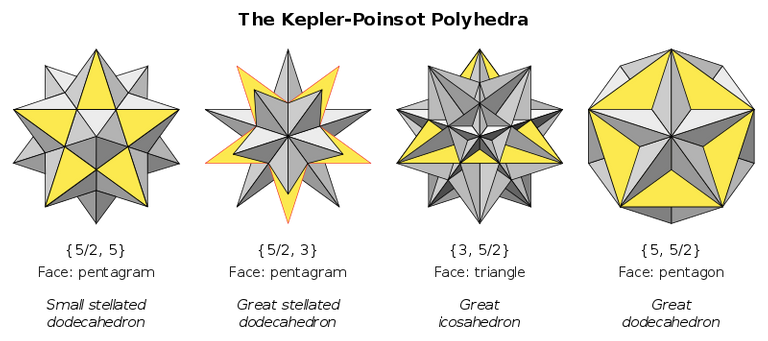
There are only four regular concave polyhedra, also called Kepler-Poinsot solids. The Lost Abenmoad would probably not have included them, since ibn Muadh al-Jayyani died long before their discovery was recorded. However, the spherical projection method he reportedly invented might work for them too. Together with the five Platonic solids, they constitute the only nine regular polyhedra. The SVG images, above, were made by Júlio Reis from a Tom Ruen design.

Kaleidoscopic construction, above, of tetrahedral symmetry in spherical projection. KaleidoTile image by Jeff Weeks. This method became the standard for uniform polyhedral projection onto the unit sphere. The Lost Abenmoad reportedly produced spherical versions of all the regular convex polyhedra by a different projection method.

WHEN MODERN GEOMETERS project a polyhedron onto a sphere, they use techniques like Schwarz triangulation and Wythoff’s kaleidoscopic construction. These techniques work well, yet have not led to breakthroughs in prime number theory. According to diagrams and hints in Benedict Benedict’s post-Soviet books, ibn Muadh al-Jayyani employed a different technique, a “zigzag method,” in the Lost Abenmoad.

This might be related to the differences of approach between ibn Muadh and Regiomontanus in proving the spherical sine law. According to N.G. Hairetdinova, ibn Muadh, in his Book on the Unknown Arcs of a Sphere, proved the law “for arbitrary spherical triangles by means of Menelaos’ theorem; he neither formulated nor proved the law for rectangular spherical triangles.” The rectangular approach was taken by “Abti’l-Wafa, Ibn ‘Iraq, al-Khujandi, al-Biruni, the Isfahan anonymous, and al-Tusi” in the East, and by Regiomontanus in Europe.

The possibility that an alternate method exists for producing spherical polyhedra is our second indication, suggesting that lost or overlooked medieval insights could make a difference, compared with modern approaches to spherical projection.

Above, Gaussian primes near the origin of the complex plane. Image by User:Hack, using Mathematica 6.0.

THE PRIMES FOUND among the ordinary natural numbers are not the only kind of prime. Other kinds are found among various “rings” of quadratic integers that dot the complex plane — integer lattices termed “imaginary” or “complex” quadratic fields.

The fundamental basis of a complex quadratic field is defined by its radicand — specifically, its radicand’s congruence in modulo 4. If the radicand has a congruence of 0 (mod 4) then it isn’t square-free and so cannot define a quadratic field.

If a radicand −d ≡ 1 (mod 4) then its fundamental basis includes a nonreal slanted axis tracing the multiples of a complex root of unity. Any complex root of unity that belongs to the field will suffice, but the chosen root is generally expressed as (1+√−d)/2, also styled (1+i√d)/2. For human viewing, it is conventional to choose this complex root of unity because it will place the slanted axis as close to vertical in the upper right quadrant as possible, so that the slanted axis is maximally distinct, visually, from the horizontal axis.

However, a competing complex root of unity can be chosen when a complex quadratic field has a 1 (mod 4) type radicand, especially when the radicand is −3. The first competing expression is e^(2πi/d). The second is (−1+√−d)/2. When d=3, these expressions coincide, representing the same point on the complex plane. And many mathematicians apparently find this coincidence irresistible. But these competing expressions are not often chosen for the values of d where they do not coincide. Occasionally e^(2πi/d) is chosen for its compatibility with polar coördinate calculations, especially when human viewing of the slanted axis is not expected.

Anyway, if a radicand −d ≡ 2 (mod 4) or 3 (mod 4) then its fundamental basis includes a nonreal axis tracing the multiples of a simpler and more straightforward expression, the square root of the radicand, √−d.

The fundamental basis of every quadratic field, regardless of radicand, also includes a simple horizontal x axis tracing the real numbers, the ordinary multiples of 1.

Consider a typical complex quadratic field of the −d ≡ 3 (mod 4) variety, the field that’s defined by the radicand −5. In ℚ(√−5), there are natural numbers with more than one proper factorization. For instance, the natural number 6 has two different proper factorizations.

6 = 2∙3 = (1+√−5)(1−√−5)

That’s right. In ℚ(√−5), the expression 1+√−5 is a complex integer, the expression 1−√−5 is a different complex integer, and their product is the plain old natural number 6.

Skeptical? Look it up here. Or, even better, visit this Wolfram widget webpage and use the widget to graph all of these expressions on the complex plane.

Use the asterisk * to represent the “times” multiplication operator when typing into the widget box. Use the formula SQRT(n) to represent the square root of some number n. To represent the square root of a negative number, you can use either SQRT(-n) or else i * SQRT(n).

Type 2 into the widget box and the widget will show you the dot where 2 belongs on the horizontal x axis — the axis of real numbers — on the complex plane. Type 3 and it will show you the dot where 3 belongs. Type 2*3 and it will show you the dot on the x axis where 6 belongs.

Type 1+SQRT(-5) in the widget box and it will show you the dot where 1+√−5 belongs on the complex plane. Type 1-SQRT(-5) and it will show you the dot where 1−√−5 belongs. Type (1+SQRT(-5)) * (1-SQRT(-5)) in the box and the widget will show you the dot on the x axis where 6 belongs. Type 2*3 again and it will dot the exact same spot.

This may be weird but it is also simple. In ℚ(√−5), 6 is a number that simply does not have a unique factorization. This is also true of 21, and of many other numbers too. Fact is, ℚ(√−5) is not a UFD, not a unique factorization domain. And ℚ(√−5) is far from alone in this. Fact is, the infinite majority of complex quadratic fields are not unique factorization domains.

Yet nine complex quadratic fields are unique factorization domains. In each of them, the ring of complex integers has its own composites and its own primes.

ℚ(√−1) is the best known complex UFD and comprises the Gaussian integers that dot the complex plane in a square lattice that includes the Gaussian primes. Gaussian integers take the form Z = a + bi where a and b are ordinary rational integers and i = √−1. The fundamental basis conforms to the complex plane in having, for its horizontal x axis, the line of real numbers where b=0, and for its vertical y axis, the line of i multiples where a=0. Like the complex plane itself, its two axes are 90° apart.

Some of the Gaussian primes — the ones where b=0 — are also a subset of the natural primes. Some natural primes, like 2 and 5 and 13, are not Gaussian primes; they are Gaussian composites. All natural primes that are also Gaussian primes have the form 4n+3, where n is a whole number.

Yet another complex UFD is ℚ(√−3), which comprises the Eisenstein integers that dot the complex plane in a triangular lattice that includes the Eisenstein primes. Eisenstein integers take the form Z = a + bω where the script lowercase Greek letter omega is often defined

ω = (−1+√−3)/2 = e^(2πi/3)

even though the conventional expression for a radicand of the −d ≡ 1 (mod 4) type would be (1+√−3)/2 instead.

Besides the horizontal x axis — the line of real numbers where b=0 — the fundamental basis of the ℚ(√−3) Eisenstein-Jacobi grid has a nonreal axis that is slanted, rather than vertical. Its nonreal slanted axis traces the 𝜔 multiples where a=0. The two axes of this grid are either 120° apart or, using the more conventional expression for ω, 60° apart.

Some of the Eisenstein primes — the ones where b=0 — are also a subset of the natural primes. Some natural primes, like 3 and 7 and 13, are not Eisenstein primes; they are Eisenstein composites. All natural primes that are also Eisenstein primes have the form 3n−1, where n is a natural number; they are also each congruent to 2 (mod 3).

Some natural primes, like 11 and 23, are both 4n+3 Gaussian primes and 3n−1 Eisenstein primes. Some natural primes, like 37 and 73 and 97, are neither Gaussian primes nor Eisenstein primes; they are composites in both Gaussian and Eisenstein-Jacobi UFDs.

Another complex UFD, more obscure but known to cryptographers, comprises the Kleinian integers, field ℚ(√−7). The fundamental basis of the Kleinian grid has, besides the horizontal x axis of real numbers, a slanted axis tracing multiples of (1+√−7)/2.

Curiously, although the forms of Kleinian primes have been discussed in mathematical literature since at least 1894, and although all natural primes that are also Kleinian primes surely have the same form, I have not been able to find that form in English online.

The drop from infinity to the finite that comes from taking all of the complex quadratic fields and then selecting only the UFDs among them is our third indication, suggesting that natural numbers can be categorized by UFD to make their infinitude more manageable.

Above, Eisenstein primes “with norm less than 500,” according to the Wikimedia file description. Image by Johannes Rössel.

AGAIN, ONLY NINE OF THE infinitely many complex quadratic fields have the property by which every composite complex integer has only exactly one single unique proper factorization. The radicands defining these nine unique factorization domains have absolute values that comprise the Heegner numbers. Each of these nine radicands defines a domain with its own primes, and some of those occur along the real axis, where they constitute a subset of the natural primes, a subset where all the natural primes have the same form. Every natural prime has its own list of the complex UFDs where it is also a complex prime, and a list of the complex UFDs where it is a complex composite, instead of a complex prime.

Here are all nine of the complex UFDs, and, for each of them, the expression whose multiples are found along the nonreal axis.

ℚ(√−1), with multiples of i = √−1 on its nonreal vertical axis.
ℚ(√−2), with multiples of √−2 on its nonreal vertical axis.
ℚ(√−3), with multiples of e^(2πi/3) or (1+√−3)/2 on its nonreal slanted axis.
ℚ(√−7), with multiples of (1+√−7)/2 on its nonreal slanted axis.
ℚ(√−11), with multiples of (1+√−11)/2 on its nonreal slanted axis.
ℚ(√−19), with multiples of (1+√−19)/2 on its nonreal slanted axis.
ℚ(√−43), with multiples of (1+√−43)/2 on its nonreal slanted axis.
ℚ(√−67), with multiples of (1+√−67)/2 on its nonreal slanted axis.
ℚ(√−163), with multiples of (1+√−163)/2 on its nonreal slanted axis.

Using the Wolfram widget mentioned earlier, you can graph any of these expressions, or mutations thereof, on the complex plane. Just use the asterisk * as your “times” multiplication sign, SQRT(n) for the square root of a number n, pi for π, i for i, and e for e.

While I have listed the nonreal axes for each complex UFD, I would rather list the form of the natural primes that are also prime in each complex UFD. However, I have not been able to find this information online in English for any complex UFD except the ℚ(√−1) natural Gaussian primes and the ℚ(√−3) natural Eisenstein primes. I appeal here to those more knowledgeable in math, who might be more skillful and successful in searching than I, to find and provide the form in question for natural primes that are also prime in each of the other seven complex UFDs.

For all nine complex UFDs, the primes nearest the zero-point origin have been beautifully mapped on this wonderful webpage. If the story of the Lost Abenmoad has any truth to it, this webpage could be likelier than any other to help you replicate Benedict’s revelation. Good luck!

The fact that every natural prime varies according to UFD in its complex prime status or complex composite status is our fourth indication, suggesting that the categorization of natural primes, according to the complex UFDs where they are not prime, could be a fruitful way to categorize their natural composite multiples that might help accelerate prime factorization.

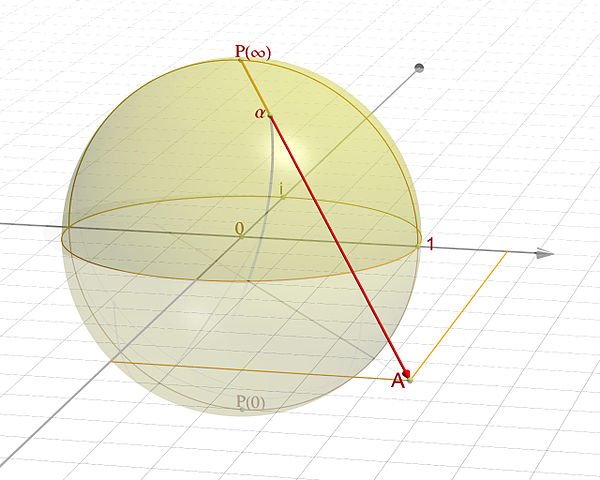
The Riemann sphere. Image by Jean-Christophe Benoist.

THE COMPLEX QUADRATIC fields that are unique factorization domains — that is, the nine Heegner fields — all map to the complex plane. Bernhard Riemann, whose prime-number hypothesis is mentioned above, was deeply fascinated by the complex plane. Moreover, he developed a model for extending the complex plane to complex infinity and compactifying the resulting extended plane onto the surface of a sphere. This compactification is called the Riemann sphere.

Since all Heegner fields map to the complex plane, they can each be extended to quadratic infinity and compactified the same way that the complex plane is compactified onto the surface of the Riemann sphere. With apologies to Gauss, who first noticed all nine Heegner UFDs, let us call these compactifications the Heegner spheres.

Using spherical polar coördinates, every Heegner sphere can be aligned with other Heegner spheres along the real numbers that they all have in common. However, correlating their nonreal axes might still pose a problem. There may be some prospect that the “zigzag method” for spherical projection of regular polyhedra, attributed to “the second book of the al-Jayyani pair,” could be key to a solution.

The prospect of using polyhedral projection to correlate the Heegner UFDs on the Riemann sphere and sort the natural composites there into categories is our fifth indication, suggesting that the “zigzag method” attributed to the Lost Abenmoad might indeed enable a modern mathematician to unlock the mystery of rapid prime factorization and related cryptographic challenges.

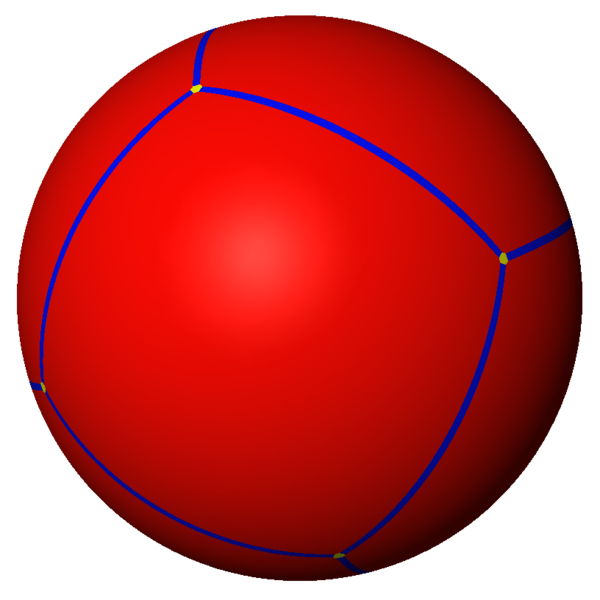
Above, spherical projection of a cube. KaleidoTile image by Jeff Weeks, presented to Wikimedia by Tom Ruen.

REASONING FROM INDICATIONS does not yield proofs or guarantees. However, in this case it does ground Benedict’s conjecture in relevant and plausible territory. If the Lost Abenmoad ever genuinely existed, Lubayd’s reminiscences and chalkboard sketches truly could have triggered a real Eureka revelation in Benedict. Even if Lubayd was faking, a real Eureka in response is at least remotely possible.

That means the cryptocoin sector could be facing a situation where new currencies need to be, not only “quantum resistant” (in some hazy future after qubit ordinator technology becomes commercially viable) but also, and more urgently, “factorization resistant” right now.

So, after the pattern of the arms race and the space race, I hope the Lost Abenmoad story can trigger a kind of multilateral math race: a factorization race, a cryptography race, for the sake of secure decentralized digital currencies and the neo-prosperity they promise.

To make that race more multilateral, I seek help from anyone who can participate in translating this and other chapters of ZigZag Sphere, including technical jargon, accurately into such languages as Arabic, Urdu, Chinese, Russian, and Hindi.

I also seek help from anyone who feels qualified to investigate, or to declare, how true or false any aspect of the Lost Abenmoad story might be. In particular, any encounters with copies or photocopies of any medieval treatise on spherical polyhedra would be of interest, and likewise any evaluation of a factorization conjecture like the one that Benedict Benedict claimed.

Questions, answers, criticisms, and suggestions are welcome in the comments.

more to come

Upvote • Follow • Resteem if you like!