
How can you divide a whole, normal circle-shaped cake into as many pieces as you can by making only 4 straight cuts with a long knife? (Provided that you do not have to have equal-sized pieces...)

How can you divide a whole, normal circle-shaped cake into as many pieces as you can by making only 4 straight cuts with a long knife? (Provided that you do not have to have equal-sized pieces...)
Guys, thanks for participating, I am waiting for @ponts to answer my question and then I will decide about the winner! It was fun to read your replies!
One horizontal cut on the top third of the cake, one horizontal cut on the bottom third of the cake, one diagonal cut from the top side of the cake to the opposite bottom side of the cake, and another diagonal cut from the opposite top side mirroring the last diagonal cut.
How many pieces will you have that way? (I have an idea, but I may have misunderstood your description, so it's better if you tell it.)
12, sorry for the delay everyone.
Impossible
I think I can get eleven. Start with drawing a diameter, and then another diameter that is the first's perpendicular bisector. Continue by drawing a line 45 degrees tilted from the first diameter but shift it slightly down to prevent it from crossing the center. Now draw a line tilted about 70 degrees from the first diameter and again lower it so that it crosses all three past lines making eleven sections. (These don't have to be exact).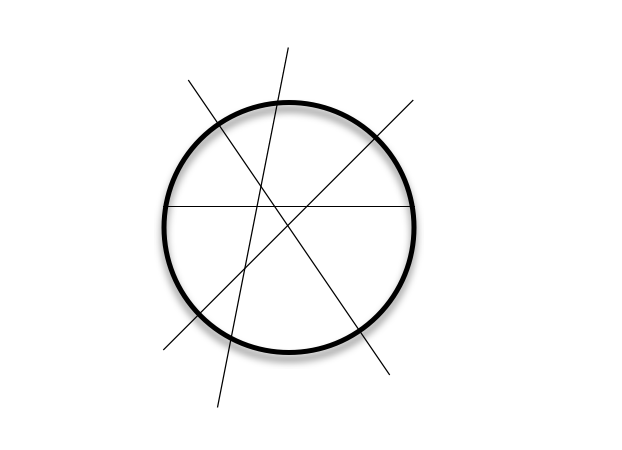
Yeah, this also seems a possible solution - actually this was the one I had in mind...
I get 16 pieces. Every time I cut the cake, I take all the resulting pieces and stack them on top of each other before making the next cut. This is much easier to do if the pieces are cut to equal size.
Theoretically this can be a good solution - you had something similar to my previous cake-problem - but it will be pretty difficult to make the cut for the fourth time (even for the third, because the pile will be too tall...) :-)
All right everybody, this was a tough and very subjective decision, because I personally liked all three solutions.
@ponts was thinking in 3D, @schwa found a solution I also had and @doughtaker was brave enough to suggest a similar solution to one of his earlier ones, which entails moving the pieces (which was not prohibited).
But as we can have only one winner and @ponts was the first one to send a correct answer, the reward goes to him.
Thanks again everyone for participating!