
Euclidean Geometry often has many surprising facts that reveal themselves through careful study.
This one always has been one of my favorites:
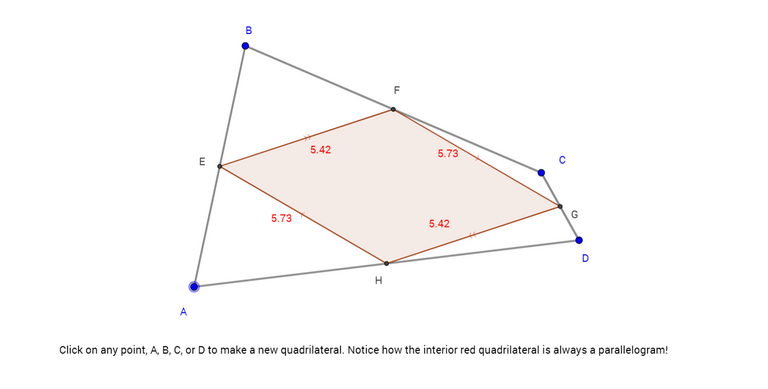
Theorem: The quadrilateral formed by joining the consecutive midpoints of another quadrilateral is a parallelogram.
This notion is absolutely stunning. That you can start with any random quadrilateral, convex or concave, and somehow out of it produce another quadrilateral that will always have some order to it.
When I was first learning this, and learning how to teach it, it was in the days of chalkboards and little in the way of interactive instructional tools. Luckily we have software today like Geogebra to assist.
Click on the image below to interact with this quadrilateral!
- You should notice when dragging around points A, B, C, or D that the interior red quadrilateral EFGH is always a parallelogram. The opposite sides are always parallel and congruent.

Want some proof? Oh, I'll give you proof!
But not like the proof you hated doing in your High School Geometry classes. Proofs don't have to be so rigid and boring. They just involve assumptions and logical conclusions from those assumptions.
As an aside, if anyone here on Steemit has a handy guide for combining LaTeX and Markdown, I would be all ears. Having to insert images over and over again is really no fun 😦.
What information is given to us?
- We have a quadrilateral ABCD.
- We have midpoints E, F, G, and H of the segments above,
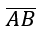 ,
, 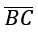 ,
, 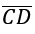 , and
, and  , respectively.
, respectively.
What do we want to show?
- We want to show quadrilateral EFGH is a parallelogram.
To show that EFGH is a parallelogram, we have to first show that their opposite sides are parallel, by definition of a parallelogram. - Or, more formally:
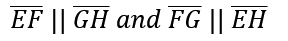
Now, lets show it!
- First a few geometric steps:

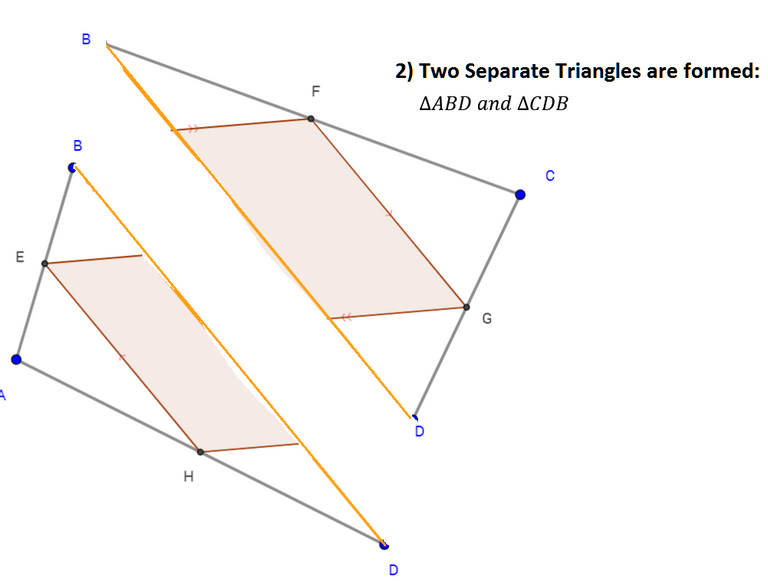
- Now, we draw upon a fact for triangles. Namely, when the midpoints of any two sides are joined to form a line segment, it will always be parallel to the side opposite. This is what is called the Midsegment Theorem.
- So, by the Midsegment Theorem, and the Transitive property, we have the following:

- To show the other two sides are parallel, follow the same series of steps but for a different diagonal.
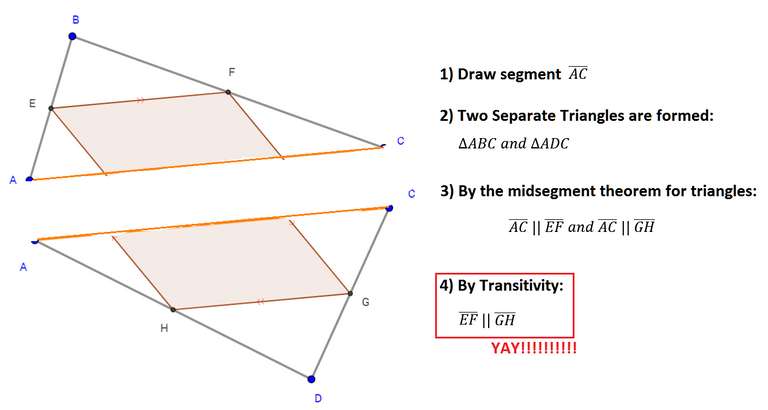
So, we accomplished what we set out to prove!
Namely, 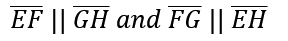
What about the concave polygon?
- It uses the same logic, but this time a diagonal could be outside the shape. Do you see the two triangles that could be formed with the diagonal connecting points A and C?
- I leave it to the reader to connect the dots....bad pun intended ;)
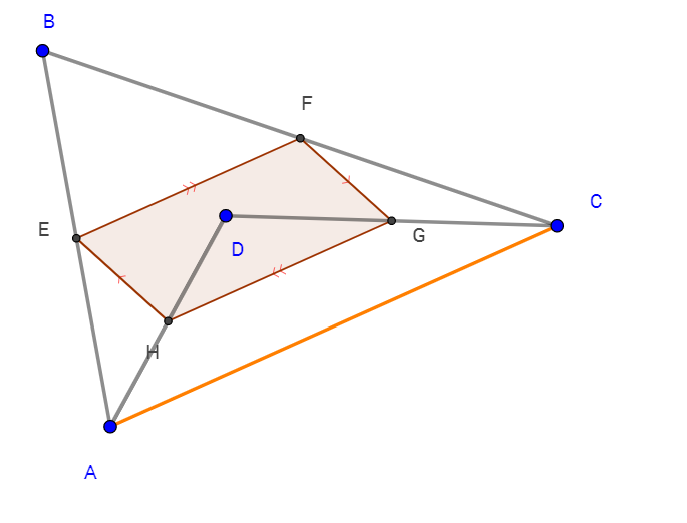
So, armed with some curiosity, and a little bit of elbow grease, we come to a spectacular conclusion.
Often in mathematics, as with life, that's all you need!
Steemit Board Awards - Click Below for More Information





This post received a 2.5% upvote from @randowhale thanks to @team-leibniz! For more information, click here!
Re LateX, I think it's time for a formal request to the forum dev; we discussed it before and it's doable.
There is a version called RMarkdown or just install mathjax.
Do you have a preference?
I don't like Markdown as it sometimes interacts badly with html, so I currently use a latex-to-html generator like codecogs. It's OK for full equations but tedious for inline snippets.
Let me know and I'll ask.
Honestly, any LateX would make me thrilled. Mathjax looks cool, but I am indifferent.
YES. A thousand times YES!!!
There is now an official request here: https://steemit.com/chainbb-suggestions/@rycharde/adding-latex-functionality-for-inline-mathematical-and-scientific-notation
If you haven't seen it, please go lend your support to the suggestion. Maybe some resteems would be good just to show how many people would like this but hae not asked. Thanks!
Neat. You have a new follower.
Thanks! Very appreciated. Glad you liked the math!
Nerd Alert - Nerd Alert
Seriously though, great post!
Thanks and Thanks! Nothing wrong with being a little nerdy :)

I really should have paid more attention in class for Geometry.
I got side-tracked by computers. Thanks for the post, it helps me round out my largely informal education :)
I don't know if you take suggestions, but I'd love to see something about fractals and specifically bifurcation diagrams if you are so inclined.
Hmmm...Sounds like a great topic for a future post! Thanks for the kind words and the awesome suggestion!
very good. nice post. :D
Oh, I didn't know this :O