Hi! I'm Giuseppe Peano, I introduce Peano system to make the life of math students miserable. Source
In 1889, Peano published a study giving an axiomatic approach to the natural numbers, showing how properties of natural numbers could be developed on the basis of a small number of axiom. Some say that the postulates should be attributed to Dedekind, but it has become generally accepted to call it "Peano's postulates".
First, we will show that our constructed natural numbers 
in the previous section follows the "Peano's postulates". Later we will show that anything satisfying Peano's postulates is, in a certain specific sense, "just like" .
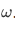To start, let's define the concept of a Peano system.
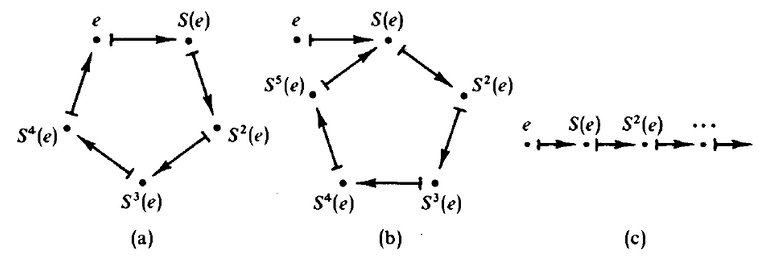
Figure 1: Any Peano system must behave like (c).
Consider a function S, and a subset A of dom S. Then A is said to be closed under S if and only if whenever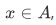 
then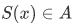
. From this, we can define the Peano system as a triple 
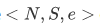consisting of a set N, a function 
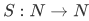, and a member 
such that the following three conditions are met:
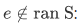this rules out loops like figure 1(a)S is one-to-one: this rules out the system like figure 1(b)
Any subset A of N that contains e and is closed under S equals N itself: also referred to as the induction postulate
The final set-theoretic condition states that no other set smaller than N itself can contain e and be closed under S.
The Peano system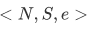 
is an expression of the universe of the system of study (N), the rules of the universe (S), and the mathematical object living in that universe (e) subjected to the 3 conditions.
As a consequence of our conditions, a Peano system must look like Figure 1(c). Our system must have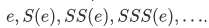 
. Visually represented by,
Let's do some work:
Our goal: we want to show that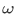 
(with the successor operation and 0) is a Peano system.
We have this theorem, which shows that some Peano system exists, given a with the successor operation and 0.
The is the restriction of the successor operation to :
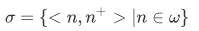
Theorem 4D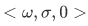 
is a Peano system.
Proof :
Since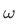 
is inductive we have
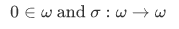
The Peano induction postulate, as applied to 
, states that any subset of A of 
containing 0 and closed under 
equals 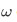itself.
It remains only to show that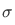 
is one-to-one. For this, we need to introduce the concept of transitive set. Note that this is different from previous definition of a transitive relation A whenever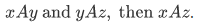 
Definition A set A is said to be a transitive set if and only if every member of a member of A is itself a member of A:
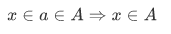
Another equivalent way of stating the previous conditions are as follows:
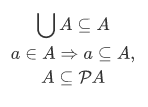
Theorem 4E For a transitive set a,
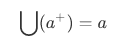
Proof
Lets calculate 
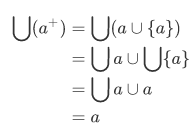
Theorem 4F Every natural number is a transitive set.
With this theorem we can now complete the proof of Theorem 4D. To do this, lets start with the idea of Theorem 4F , consider the case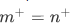 
for m and n in 
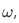, then
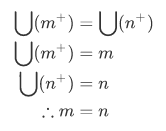
Thus, we've shown that
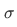is one-to-one.
Theorem 4G The set 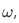is a transitive set.
The implication of this theorem is that every natural numbers it itself a natural numbers or in a more detailed way of saying: every natural number is the set of all smaller natural numbers.
Disclaimer: this is a summary of section 4.2 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshots from generated latex form using typora
Thank you for reading ...
Nice post ! You got 15.38% upvote from @flymehigh. Earn free sbd/steem daily by delegating(renting) your SP. We share high return, click here to delegate your sp to flymehigh if you don't know, how to earn passive income by delegating your SP click here for more info Join our discord You can promote your posts. Thanks.
@tipu status
Hi @sinbad989! Here is your @tipU service user data:
@tipu profit 5000 sp delegated
Yesterday 5000.0 STEEM POWER delegated or invested gave payout of:
0.07 SBD + 2.301 STEEM (0.73 USD), APR: 18.39% .
Delegation link: steemconnect 5000.0 SP delegation to @tipu.
Please note that your profit can be slightly different (depending on the payout time).Check out https://www.steemprofit.info to compare @tipU with other services.