Nowy język
Dalsza część Lamentu to biadolenie Autora nad matematyczną nomenklaturą, którą się katuje uczniów. Paul Lockhart dziwi się np. dlaczego w szkole nie pozwala się używać sformułowań typu „kształt o czterech krawędziach”, a zamiast tego oczekuje się nazwy „czworobok”. Autor wsadza do jednego worka wszystkich, którzy dbają o język matematyki i jednoznacznie ich potępia. Tutaj akurat bym się nie zgodził, bo według mnie da się przemycić nomenklaturę matematyczną nawet w łamigłówkach i zabawach. Dodatkowo, wiele podstawowych symboli matematycznych występuje powszechnie chociażby w kalkulatorach. Ciężko byłoby przyspieszyć sobie obliczenia nie znając podstaw matematyki.
W praktyce więc program matematyki okazuje się nie tyle sekwencją tematów, co raczej sekwencją notacji. Matematyka jawi się jako sekretna lista tajemniczych symboli i reguł ich stosowania. Maluchom daje się „+” oraz „÷”. Dopiero później zasługują na „√” oraz „x” i „y”, i alchemię nawiasów. Wreszcie przychodzi czas na indoktrynację z użyciem „sin”, „log”, „f(x)”, ale jeśli zbiorą dobrą opinię, to nawet „d” i „∫”. Wszystko to bez żadnego pojedynczego doświadczenia w matematycznej twórczości.
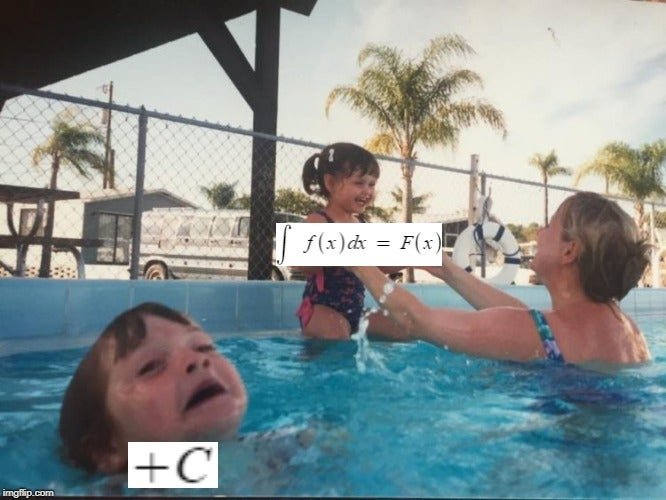
Nigdy nie zapominaj o stałej całkowania
Według mnie, na pewnym etapie nauczania uczeń jest w stanie dostrzec logikę i spójność języka matematyki. W takiej sytuacji, dawka „nowych słówek” jest po prostu dodatkowymi puzzlami, które trzeba poukładać analogicznie do poprzednich. Nie znam nikogo kto by miał problem z wywołaną alchemią nawiasów. Ponadto, symbole matematyczne takie jak „sin”, „log”, „d” i „∫” nie są wzięte z powietrza – są skrótem od pełnych wyrażeń ([sin]us, [log]arytm, [d]erivative) lub nawet kształtem podpowiadają swoją definicję (znak całki „∫” jest takim bardziej rozciągniętym „S” – oznacza [s]umę). Mogę jedynie domniemywać, że Autorowi chodziło o mnogość niepotrzebnych symboli ubranych w kolejne działy podręcznika. Tutaj bym się zgodził, aczkolwiek według mnie, problemem nie jest bogaty język matematyki, a to w jaki sposób jest on podawany uczniom. Wydaje mi się całkiem możliwym, aby przedstawić nowe symbole na zasadzie odkrywania, podróży w nieznane. Często nowy symbol implikuje zmiany w zadaniach/łamigłówkach, które były wcześniej rozwiązywane. Myślę, że to jak ów symbol wpływa na finał tych samych zadań, może wydawać się ciekawe. Taki proces rozwiązywania zadań zastosowałem w praktyce ze studentami – jednakże zmienną była tutaj użyta metoda rozwiązywania, a nie modyfikacja samego zadania. Autor cytuje słowa Bertranda Russella:
„Zmuszono mnie do nauki na pamięć: ‘Kwadrat sumy dwóch liczb jest równy sumie ich kwadratów powiększonej o ich podwojony iloczyn’. Nie miałem bladego wyobrażenia, co to w ogóle znaczy, a kiedy nie umiałem zapamiętać słów, nauczyciel walił mnie książką po głowie, co jednak w żaden sposób nie wzmagało mojego intelektu na tyle, bym był w stanie je zapamiętać.”
W dalszej części Paul Lockhart usprawiedliwia nauczycieli. Muszę przyznać, że czekałem na te słowa, bo wcześniej nie zostawiał na nich suchej nitki, a nie jestem przekonany o 100 %-owej odpowiedzialności nauczycieli. Paul Lockhart wini system, który tworzy nauczycieli i podstawę programową. Jednakże jedynymi osobami, które mogą złamać ten trend są właśnie nauczyciele i w tym tkwi ich odpowiedzialność – nie ma co liczyć na to, że pomoc przyjdzie odgórnie. Tylko praca u podstaw.
Geometria narzędziem szatana
Nie ma nic bardziej irytującego dla autora zjadliwej krytyki, jak kiedy cel całego jadu, który z siebie wypuszcza oferuje mu się w charakterze poparcia jego tez. Nigdy wilk w owczej skórze nie jest tak podstępny, a fałszywy przyjaciel tak zdradziecki, jak to się zdarza z geometrią w gimnazjum. Ta geometria jest tak piekielnie niebezpieczna dokładnie dlatego, że rzeczywiście stanowi próbę wprowadzenia uczniów w sztukę argumentacji.
Autor określa geometrię narzędziem szatana ze względu na potencjał, który tkwi w tej gałęzi matematyki. Potencjał, który jest tłamszony od pierwszych minut lekcji wprowadzającej. Dlatego właśnie szkoda, którą się wyrządza uczniom jest w tym wypadku największa spośród szkód wywołanych przez inne karkołomne przedstawianie poszczególnych działów matematyki.
Inne dziedziny mogą co prawda ukrywać pięknego ptaka, zamykać go w klatce, ale na lekcjach geometrii jawnie się go torturuje.
Piękny dowód powinien wyjaśniać – powinien być zrozumiały, głęboki i elegancki. Dobrze skonstruowany i dobrze napisany dowód powinien smakować jak łyk źródlanej wody, być jak smuga światła – powinien ożywiać duszę i oświecać umysł. I powinien być czarujący.
Pamiętam dowody przeprowadzane przez mojego nauczyciela z matematyki w liceum. Nie wiem jak inni, bo wyłączałem się wtedy zupełnie, ale ja byłem zahipnotyzowany. Najczęściej w klasie zapadała cisza, nauczyciel też ściszał głos i następował finał. Majstersztyk. Dlatego doskonale rozumiem o czym mówi Paul Lockhart – nauczyciel, który potrafi z takim zapałem udowadniać tezy, musi być nauczycielem, który sam niejednokrotnie zmagał się z problemami matematycznymi i je rozwiązywał. Na tym polega odpowiedzialność matematyka.
Swego czasu, jeszcze jako student, brałem udział w Maratonie Zadaniowym Uniwersytetu Wrocławskiego. Genialna zabawa – rozwiązuje się zadane przez użytkownika zadanie i jeśli rozwiązanie jest poprawne, proponuje się kolejne zadanie innym uczestnikom maratonu. Nawet coś tam udało się wygrać.

Wracając do geometrii. Lament nad tą gałęzią matematyki zaczyna się od zderzenia z nomenklaturą. W sumie racja – notacja jest dość wysokim progiem wejścia i konsekwentnie stosowany język matematyki może sprawiać problemy. Pamiętam jednak, że mój nauczyciel matematyki nie męczył nas aż tak skomplikowanym zapisem, a skupialiśmy się na problemach. I tutaj może ten lament odbiegać od tego co mamy w rzeczywistości.
Podsumowując, w mojej ocenie, przyjemniej jest słuchać kogoś, kto posługuje się nienaganną polszczyzną, bo mogę się czegoś nauczyć. Podobnie z językami obcymi. I tak samo z matematyką. Trzeba jednak przyznać, że chodzą po ziemi tzw. gramatyczni naziści, którzy przesadnie dbają o higienę języka. Pytanie czy warto zadać sobie trud, żeby posługiwać się danym językiem aż tak perfekcyjnie? Wydaje mi się, że w ogólności nie. Natomiast jeśli jesteśmy na zaawansowanym poziomie nauki danego języka, to z samej ciekawości czasami zdarza się sprawdzić jakieś językowe kruczki lub idiomy. W matematyce jest podobnie – torpedowanie nową notacją uczniów szkoły podstawowej mija się z celem, ale na poziomie liceum lub studiów, gdy zasób słów się zwiększy, dawka novum nie jest żadną trucizną.
Zdjęcia:
[1] — mem z internetu
[2] — mem z internetu
Sam z własnej edukacji matematycznej pamiętam, że najwięcej zabawy miałem z konstrukcją.
A jeśli chodzi o program, to myślę, że powinno szukać się złotego środka — z z jednej strony czysta matematyka, z drugiej jakieś pokazanie odniesienie do życia poza szkołą w stylu kalkulacji finansowych, namiastki obliczeń wykonywanych przez inżynierów z różnych dziedzin itp.
Pamiętam swoje zdziwienie, gdy już jako dorosły człowiek oglądałem jakiś edukacyjny filmik dotyczący chemii i było pokazane obliczanie jakiegoś stężenia. W pewnym momencie pojawiło się równanie kwadratowe i myśl, że w szkole brakło właśnie przełożenia tego na coś bardziej namacalnego.
I może dlatego to takie trudne, bo złoty środek zmienia swoje położenie na przestrzeni poszczególnych klas. W podstawówce trzeba dzieci jakoś zachęcić do matematyki poprzez łamigłówki, zabawy, ale w liceum już niekoniecznie - tam można się już co nieco pobawić czystą matematyką :)
Właśnie tutaj też może być różnie, bo ze szkoły średniej i z perspektywy ucznia, i później z perspektywy nauczyciela, pamiętam narzekanie na nieprzydatność całego nauczania.