I just noticed a second suspicious fact in your graph. According to the nonrefereed article, the IQ standard deviation for Asians is much lower than it is for whites. In your graph, the Asian standard deviation appears to be noticeably higher. (In your graph, the Asian curve is lower and broader than all of the other curves.)
I suspect that your graph comes from one particular study, while the refereed source that I cite is a survey article that reviews thirty years of research.
the IQ standard deviation for Asians is much lower than it is for whites
really?
In statistics, the standard deviation (SD, also represented by the Greek letter sigma σ or the Latin letter s) is a measure that is used to quantify the amount of variation or dispersion of a set of data values.[1] A low standard deviation indicates that the data points tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the data points are spread out over a wider range of values.
kinda like this?
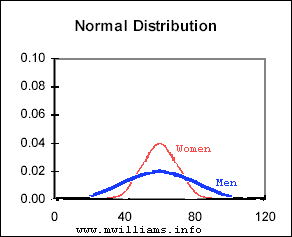
is it right to say that males are more likely to score better than females in math, when it's also true that they're more likely to score worse?
Exactly. Here's another quote from the unrefereed Radical Capitalist article: "Asian IQ scores cluster around the mean; thus, the cognitive variation among Whites produces more geniuses, but also more morons."
"Asian IQ scores cluster around the mean;
in my not so humble and somewhat uneducated opinion (math is hard and I only took one stat class)
that is a non sensical statement.
perhaps there is good reason that the article was not refereed...they found math to be hard also...
I agree that they express the idea imprecisely, but if you read the quote in its context, the meaning is clear. Increase the standard deviation for a given mean and you would get both more geniuses and more morons. They are clearly claiming that the standard deviation for Asians is lower.
Such a claim is plausible on genetic grounds. I read that one out of five Asians have a common ancestor, according to their DNA, and that common ancestor is hypothesized to be Gengis Khan, who reportedly copulated with a different woman each day for decades of his reign.
math is fun
just guessing..but it would seem that the size of the population matters.
Sampling his conquered population must certainly have been fun for Gengis Khan, and, as they say, "size does matter".
Slightly more seriously, any actual living population, say of Caucasians, is thought of as having been drawn independently, one at a time, from some imagined process such that the drawings are characterized by that formula for a normal probability density function.
If that is true (that the process really produces normally distributed drawings), then mathematics can be used to prove that the sample mean is an unbiased estimator of the population mean. It turns out that the "adjusted sample standard deviation", which is calculated using N-1 rather than N (where N is the sample size) is an unbiased estimator of the population standard deviation.
So you can get an unbiased estimate of the population standard deviation from a sample of any size with at least two observations, but of course the estimate will be more reliable for greater sample sizes.
any actual living population, say of Caucasians, is thought of as having been drawn independently, one at a time, from some imagined process such that the drawings are characterized by that formula for a normal probability density function.
I can't get my head around that statement.
what does it mean?