During the summer I had the opportunity to attend a talk by Professor Yaron Silberberg, an Israeli physicist at the Weizmann Institute. He’s made considerable contributions in nonlinear optics, integrated optics, optical solitons integrated optics and much more. That particular talk was on his recent work on speckle correlation and scattered wavefront correction imaging. I thought I’d dissect some of the science/tools used in the latter, which allowed his group to image live objects by using walls as mirrors.

To better grasp how this can be achieved, we must first understand what genetic algorithms and spatial light modulators are.

Genetic algorithms
Genetic algorithms are optimization methods that evolve and adapt to a set of constraints over multiple iterations. For each successive “generation”, random parameter modifications are applied the best performing object based the predetermined optimization function. In cases where the end goal is well defined, this evolutionary process can easily outperform humans at determining optimal parameters. The field of genetic algorithms is great on its own, but its details have been discussed here in the past, so I’ll just leave you with a short list of captivating examples where they were successfully used:

Flexible Muscle-Based Locomotion for Bipedal Creatures
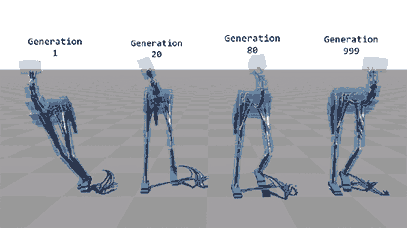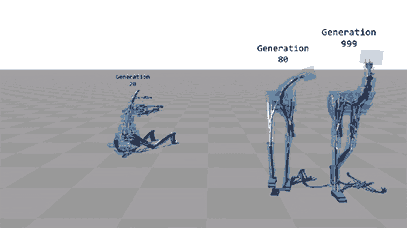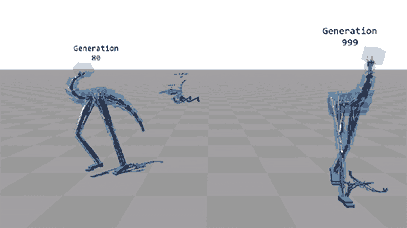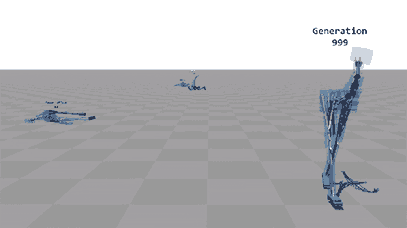

Browser based random two-wheeled shapes evolving into cars


MarI/O

Spatial light modulator
Spatial light modulators, or SLM’s, are, as their name describes, computer controlled objects that modulate the spatial distribution of light. They're used both for transmission and reflection applications. They usually consist of an array of cells or pixels (similar to a checkerboard with controllable white/black square locations) that can individually induce a phase delay and/or change the reflection or transmission intensity of the incoming light. For those less familiar with phase, consider the following animation:

In that example, we can see the wave-front gets distorted as it passes through the SLM (cross-sectional view). The grey cells in this diagram have a higher index of refraction, effectively slowing down the wave-front locally. Specifically, this shows that if the shape of the wave-front is known in advance, one can use an SLM to tune it to a desired shape. In diagram above, a flat wave-front can be recovered from using the right pixel combination (check mark), but not otherwise (red cross).
In the case of intensity modulating SLMs, the grey pixels are made in a way that partially or totally blocks the light, instead of simply slowing it down.
Uses of spatial light modulators range from the creation of incredibly complex laser beam polarization profiles to holography to wave front correction. The latter will come in handy later.

How it works
We've quickly overviewed two essential tools for controlling light. Combine them in the right order, and you just gained a super power: one that allows you to use walls as mirrors and see through thin scatterers like egg shells. Let’s take a look at a possible setup in the transmission case:
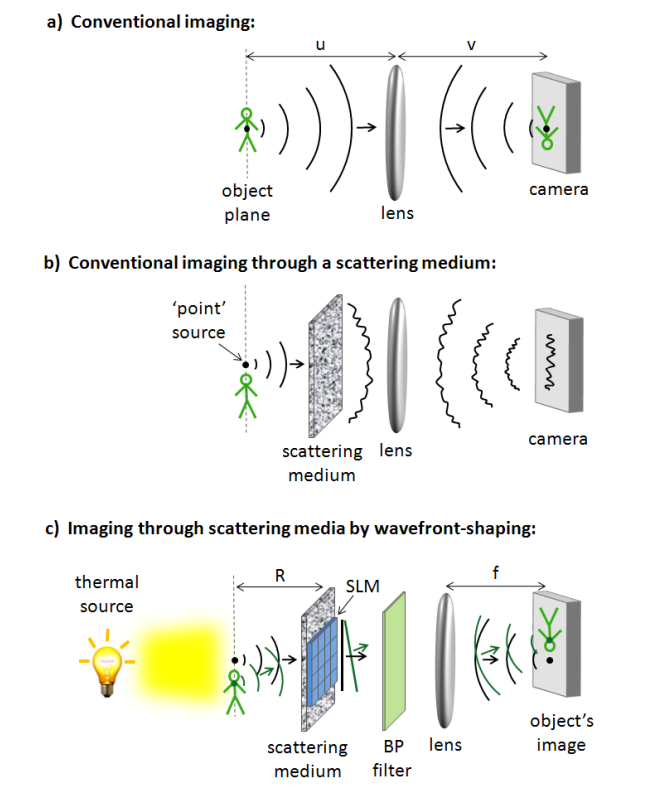
As described, a) represents a simple imaging system. In b), the scattering medium is added. As you can see, it distorts the original wave-front in such a way that the perceived image is indistinguishable from noise. Just like most surfaces around you, this scattering glass is covered in microstructures that diffuse light and appears to be of a single color instead of making it being perfectly transparent or reflective. In c), an SLM is added to allow for wave-front shaping correction. That element is added to attempt to “cancel” the effect of the of the scatterer by precisely choosing how each cell interacts with light. Since this correction can only be valid for a small bandwidth, a bandpass filter is added. [1]
So how exactly do we know what pixel distribution we need to correct for a scatterer? This is where the genetic algorithm comes in. It's used to “learn” the best pixel configuration for the SLM by evolving over multiple iteration and building on its past experience. First, we start with a point source at a distance R from the SLM. This looks like subimage a) in the following picture. Quite messy as you can see:

From this, a single speckle in the output image is selected. The task given to the genetic algorithm is then to simply try to maximize the intensity around at the chosen point. It first starts with a random pattern, but after a few generations, the speckle intensity ends up being enhanced 800 times, as shown in image b). The contrast of the image turns out to be proportional to the number of pixels in the SLM. [1]
Once that’s done, any object in the vicinity of the optimized point source will be imaged live. The end result of can be seen in d) for the object shown in the insert of c) (letter A).
In the same way, the process can be applied to walls or paper to recover an image lost due to scattering. Here it is with paper
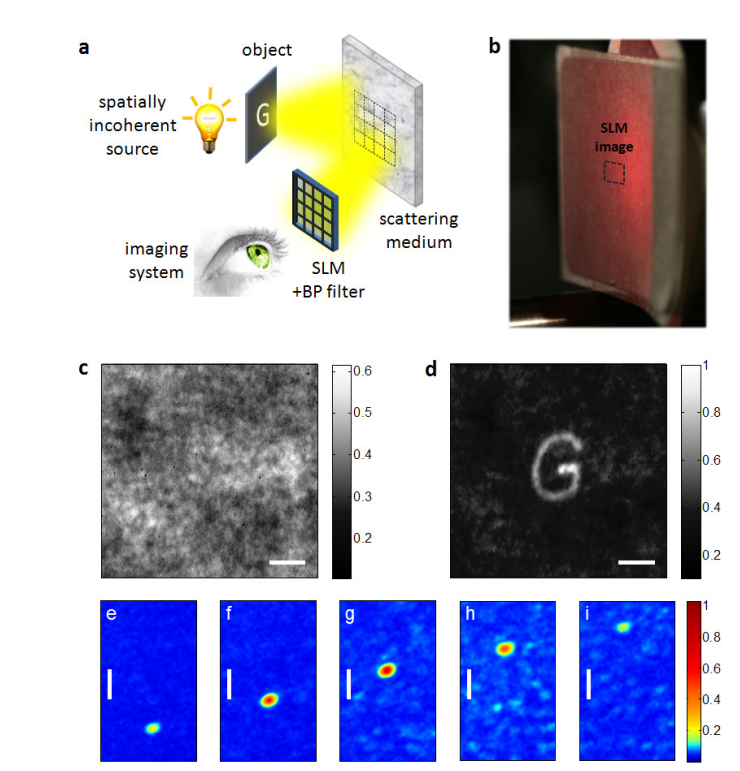
In a) is displayed the experimental setup, b) a picture of the paper used (scatterer) and c) the image seen with the naked eye and the recovered image of the letter G in picture d). [1]
The beauty of this relatively simple technique is that it doesn’t require the use of coherent light (lasers). It could be in a variety of applications that necessitate imaging or microscopy through turbid tissue or inhomogeneous media.
What if we could one day see the inside of an egg and observe a chick grow live, in high resolution, thanks to the ability to completely cancel out the effects of shell scattering? We’re not quite at that point yet, but this sure brings the possibility closer than ever before.


If you liked this type of article, make sure you follow me @owdy
Any questions, comments? Leave them below or get in touch with me in the chat!
I didn't quite fully grasp exactly what is involved, but what I get is this is an amazing advance for both photographic imaging and holography. Since I learned about radiosity shading in computer graphics light simulations, now and then I spot pseudo-reflections on non-polished surfaces that show colours from objects I can't see. I imagine that it should be possible to reassemble the reflections into a coherent image with the right processing.
Just so I understand this correctly, this is one of the core elements of this technique right?
Pretty much!
A mirror is purely specular reflection, so you end up with a perfect image of the object. If you had a wavy mirror, you'd get a wavy image. Now, imagine that you wanted to cancel out the effect of the waves and get a perfect image back. You could create what would essentially be a "negative" of the shape of the mirror. That way, each light "beam" would get corrected back to its original position, forming a perfect image again.
The challenge here is that the waves on your mirror are extremely small and complex, so it's impossible to create a negative since no one knows exactly what wavy pattern we're dealing with. One way to solve this is to use a known image (point source), produce a random "negative" and evaluate its performance in recreating the object. We then keep the best parts of that negative and slightly modify the rest to see how that improves the image. Repeat that process multiple times and you end up with a very good negative made simply of an array of pixels (SLM). Once your negative has been optimized for a point source, it will work for any image.
In a way, decoding the scattering medium is similar to playing a very difficult game of Mastermind, where the codemaker is nature and the codebreaker is a computer.
Hope this clarifies it, thanks for asking!
Yeah, you could use a cryptographic analogy very well. The texture and specular properties of the surface are like the secret key, but you can identify part of it directly from an image of the surface by itself. Teasing apart the parts of the surface that provide information, and from which angle this information originates, is the puzzle part. With a very high resolution image, it gets a lot easier because you can infer textural patterning in the nonspecular reflective surface.