Saludos a toda la comunidad científica y académica de Steemit, luego de varias semanas sin publicar (producto de dificultades de conectividad) nuevamente me incorporo a la actividad steemiana con el desarrollo reflexivo de una temática de mucha importancia para los cimientos de la Matemática, en este sentido, en la presente publicación se abordarán las nociones fundamentales relativas a las Leyes de Composición Interna, una conceptualización matemática que viene a aclarar muchos escenarios confusos que se han generalizado y popularizado al punto de ser aceptado por tradición. Para ello, es conveniente tener presente algo que hemos aprendido desde nuestra infancia cuando comenzamos a aprender Matemática, esto es, las operaciones matemáticas Suma, Resta, Multiplicación y División en tanto que los planteamientos a continuación versarán en aclaratorias al respecto de éstas.
Quiero resaltar, que la primera vez que estudie los saberes que se detallarán en este post, fue en el tercer semestre de mi carrera de Educación mención Matemática y a medida que el profesor explicaba sentí como si se disolvieran velos de realidad errada en mi mente, recordando como lo había aprendido en cursos preuniversitarios y experimentando una fuerte necesidad de desmontar lo anterior para apropiarme de los conocimientos de la manera correcta. Esto además me hizo pensar en la necesidad de repensar la educación en Matemática, en tanto que es común pensar que alguien no va a comprender un determinado concepto de esta ciencia por su naturaleza abstracta y es que esta forma de ver las cosas es lo que nos tiene sumergidos en la repetición recursiva de formas erróneas de enseñarla generalmente subestimando al estudiante, entonces dejamos de llamar las cosas por su nombre considerando un lenguaje elemental que pensamos pueda ser comprendido por los aprendices, perdiéndose en este absurdo proceso la formalidad de una ciencia tan importante para la vida de los seres humanos.
Adicionalmente, lo que me propongo mostrar a continuación (y lo que les he presentado en publicaciones anteriores de Matemática), en muchas oportunidades cuando trabajé en el nivel de bachillerato desde el primer año de escolaridad, lo procuré facilitar llamando las cosas por su nombre, tal como las aprendí en mis estudios universitarios y debo decir gratamente que los mitos y leyendas que aseguran que un estudiante de edad adolescente no entiende lo abstracto son totalmente falsos, en ese entonces, me di cuenta de que los que estamos mal somos los educadores al tener tantos prejuicios infundados, y probablemente por esas falsas creencias hemos sido responsables de que la juventud no se sienta llamada mayoritariamente por el estudio de la Matemática y carreras afines. En mis experiencias, muchos de los estudiantes que tuve en esas oportunidades escogieron opciones universitarias en áreas científicas afines a esta ciencia, así que el llamado es a dejar los prejuicios y confiar en que ellos son capaces de llegar lejos y alto.
Dichas estas breves reflexiones introductorias, me dispongo entonces a presentar la temática Leyes de Composición Interna cuya importancia radica en la preservación de la formalidad del lenguaje matemático y en ese sentido se hará el esfuerzo por presentar los saberes de forma detallada y descriptiva de manera tal que se garantice la adecuada comprensión y se materialice el llamado interior a dar pasos en la dirección correcta. Es de hacer notar que este material se construye con propósito didáctico y reflexivo para apoyar la enseñanza del Álgebra, subárea de gran valía en el ámbito matemático, lo cual como valor agregado hace que Steemit sea una potencial plataforma educativa para el intercambio formativo entre educadores y estudiantes de los diferentes niveles educativos. Se les invita a continuación al disfrute académico de las nociones previamente identificadas. Comencemos.
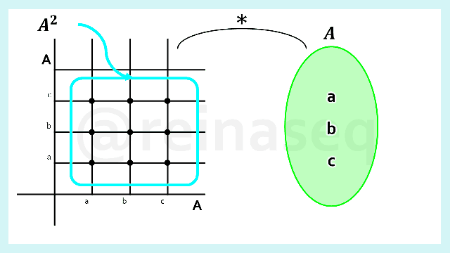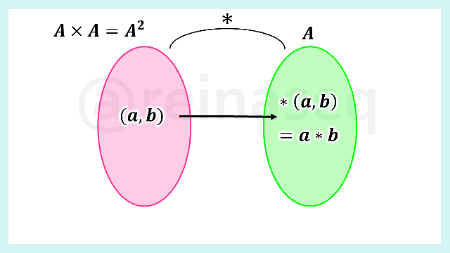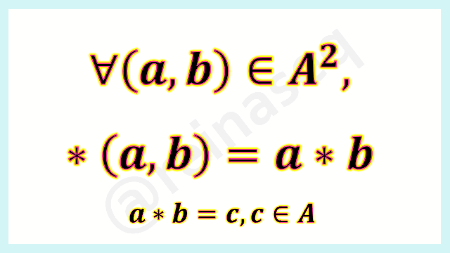
En esta parte se presentará la teoría vinculada al concepto de Leyes de Composición Interna, para lo cual recomiendo repasar como conocimiento previo la concepto de Funciones, en tanto que precisamente una ley interna es una función definida con cualidades muy particulares. Recordemos que para definir una función es necesario considerar un conjunto de partida y un conjunto de llegada en primer lugar, por lo cual para el concepto que nos ocupa debemos considerar el escenario para el recorrido como sigue:
- Conjunto de Partida: A×A=A2, Producto Cartesiano definido en un mismo conjunto A≠∅.
- Conjunto de Llegada: El conjunto A≠∅.
Ya teniendo claro el contexto procedemos a plantear la expresión matemática que define la función ley interna como sigue
Animación creada por @reinaseq (más detalles al final del post)
Ahora bien, se puede apreciar claramente la representación gráfica y simbólica vinculada al concepto, sin embargo a manera de clarificar aún más lo allí expresado se detalla la siguiente explicación:
La función ley interna es *:A2⟶A.
Los elementos del conjunto de partida se simbolizan (a,b), es decir, son pares ordenados que pertenecen al producto cartesiano A2.
Los elementos del conjunto de llegada se obtienen mediante la expresión (a,b)= a * b
La expresión a * b (se lee a compuesto con b) es un valor numérico c∈A y se obtiene de componer las coordenadas del par ordenado (a,b).
Se entiende que se trata de una ley de composición interna porque el resultado es un elemento que pertenece al mismo conjunto no vacío A.
En resumen, se tiene que: la imagen del par ordenado (a,b) a través de la función ley interna *:A2⟶A es igual a la composición de las componentes del referido par ordenado y tal composición pertenece al conjunto no vacío A.
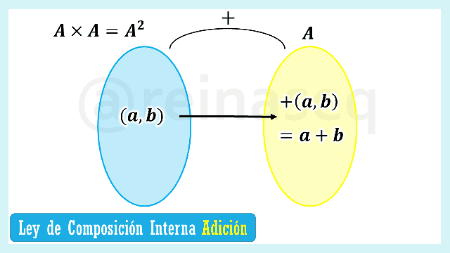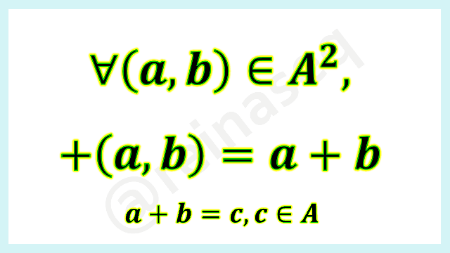
Ahora bien, una vez aclarada la definición de Ley de Composición Interna, es válido destacar que en ámbito matemático destacan dos de éstas en particular, las cuales son:
- Ley de Composición Interna Adición
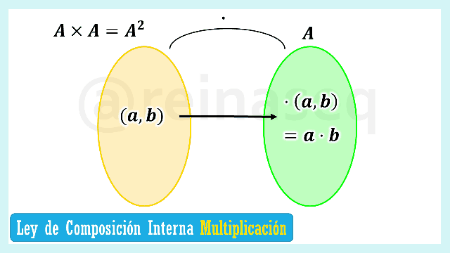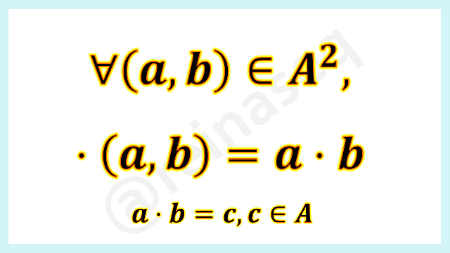
- Ley de Composición Interna Multiplicación
Las mismas al definirlas desde la formalidad del caso general ya planteado tenemos
Animación creada por @reinaseq (más detalles al final del post)
Animación creada por @reinaseq (más detalles al final del post)
En atención a esta realidad, se hace necesario destacar las siguientes precisiones:
- Cuando se habla del caso general el lenguaje idóneo es asumir que los elementos involucrados se componen. Ya considerado cada caso particular el manejo semántico se adapta a cada ley de acuerdo a su naturaleza: en el caso de la ley adición lo correcto sería decir que los elementos se adicionan y en el caso de la ley multiplicación corresponde afirmar que los elementos se multiplican.
- Cuando consideramos la ley adición los elementos que intervienen en el proceso se conocen como sumandos y el resultado de la adición (es decir, composición mediante la ley adición) se le denomina suma. En este sentido, es relevante aclarar que la suma es un valor numérico por lo tanto no verifica propiedades, las cumple o no la ley interna en cuestión dependiendo del conjunto numérico donde accione.
- En cuanto a la ley multiplicación los elementos involucrados en el proceso se conocen como factores y el resultado de multiplicar dichos elementos se le denomina producto. Asimismo, de manera análoga a la ley adición es claro que el producto es un valor numérico por lo cual no verifica propiedades, como de hecho las cumple o no la ley multiplicación de acuerdo al contexto numérico donde interactúe.
En este punto se preguntarán ¿por qué no se ha hecho referencia a la resta y la división o a la sustracción y división?
Es claro que para dar respuesta a este cuestionamiento debemos seguir avanzando en la fundamentación teórica, por lo cual pasaremos a detallar las propiedades y elementos distinguidos que podría verificar una Ley de Composición Interna. Refiriéndonos al caso general tenemos lo siguiente
Como se puede apreciar en la imagen no aparece la propiedad de clausura o cerradura y es por el hecho de que la misma viene dada por la definición general de Ley de Composición Interna ya planteada, en la cual resulta evidente que al componer dos elementos de un conjunto no vacío A el resultado pertenece al mismo conjunto, de allí la connotación de ley interna la cual se fundamenta claramente en la clausura.
Ahora nos interesa visualizar como se representan las propiedades y elementos distinguidos en los casos particulares adición y multiplicación para lo cual es conveniente observar la siguiente representación:
Ciertamente, para los que ya han transitado por sus estudios de bachillerato la información resulta familiar, no obstante, es conveniente recalcar lo siguiente:
- El elemento neutro en la ley adición es el 0 (cero) y el mismo es único para todos los elementos del conjunto, esto es, no existe otro elemento neutro y la demostración (por Reducción al Absurdo) puede ser consultada en los textos de referencia al final del post.
- Se puede observar que los elementos simétricos en la adición se denotan (-a), es decir, utilizando un guion a la izquierda de valor numérico. Generalmente los elementos simétricos en la ley adición se denominan de forma particular como elementos opuestos. Es muy importante destacar que en los conjuntos numéricos donde existen éstos para cada elemento del conjunto, el mismo es único, esto es, un elemento cualquiera del conjunto tiene uno y sólo un elemento opuesto.
- El elemento neutro en la ley multiplicación es el 1 (uno) y al igual que en la ley adición éste es único para todos los elementos del conjunto, asimismo, esta afirmación es demostrable (consultar textos de las referencias).
- En el caso de la ley multiplicación los elementos simétricos se representan 1/a, esto es, en forma de fracción. Los mismos se denominan de forma particular como elementos inversos. De manera similar a la ley adición, se cumple la unicidad de los elementos inversos.
Es probable que se haya notado que en las diapositivas donde se muestras las propiedades y elementos distinguidos para los casos particulares que no se encuentra la propiedad distributiva, y es que por el hecho de que la misma involucra a las dos leyes internas debe representarse en una imagen separada, la cual pueden observar a continuación
Como puede apreciarse, la distributividad tanto a derecha como a izquierda se plantea de la ley multiplicación respecto de la ley adición, no obstante si se presentara de la adición respecto de la multiplicación bastaría con un sencillo contraejemplo para comprobar que en ese sentido no se cumple.
Algo que es importante resaltar es que las propiedades y elementos distinguidos de una ley de composición interna al estar planteadas mediante un símbolo de igualdad nos indica que las mismas son aplicables tanto de izquierda a derecha como de derecha a izquierda, esto se aclara en tanto de que generalmente cuando este saber es facilitado en las aulas de clases se acostumbra a enfatizar la aplicación de las mismas de izquierda a derecha restando importancia a su aplicabilidad en sentido contrario, esto ha hecho que a pesar de ser algo elemental en el nivel conceptual no se entienda con claridad lo que significa el símbolo de la igualdad y esto conlleva a erróneos recursos emergentes de aprendizaje que distorsionan el saber en su formalidad matemática, por ejemplo, en el caso de la distributividad se entiende muy bien cuando se aplica de izquierda a derecha pero cuando se hace en sentido contrario no se enfatiza que se trata de una operatividad propia de la propiedad distributiva y lamentablemente se termina llamando factor común.
En líneas generales, en cuanto al caso particular, sólo se puede hablar de la ley adición y la ley multiplicación con operatividades dadas por las propiedades ya planteadas, ahora bien, tenemos una pregunta pendiente y a continuación se expondrá una aclaratoria reflexiva a respecto.
Desde que tenemos uso de razón, es decir, desde que comenzamos a estudiar matemática en la escuela nos dicen y recalcan que existen cuatro (4) operaciones fundamentales: suma, resta, multiplicación y división. En el mejor de los casos cuando llegamos al bachillerato, es probable que nos encontremos con algún docente del área que nos presente (aunque con el mismo enfoque tradicional) tal situación indicándonos que las operaciones son: adición, sustracción, multiplicación y división, así lo reafirmamos y en consecuencia accionamos de acuerdo a la perspectiva del que nos está formando, porque pensamos que debemos llenar las expectativas de la persona que a fin de cuenta nos va a evaluar, así que no nos queda otra opción que aprender de la manera en que nos están enseñando.
Ahora bien, ocurre que cuando se llega al nivel universitario y escogemos una carrera profesional en la cual debemos conocer con lujo de detalles la ciencia Matemática (en mi caso Educadora en Matemática) y conocemos por primera vez el maravilloso concepto de Leyes de Composición Interna nos damos cuenta de que tenemos que desaprender para aprender la realidad como debe ser, con la aspiración (fallida en muchos casos) d que seamos multiplicadores de la formalidad matemática en los diferentes contextos donde nos desenvolvamos.
Dicho esto, comencemos a hablar de la resta o sustracción con el siguiente argumento inicial, si fuera correcto hablar de estos conceptos como ley deberíamos al menos tener claro que la resta es el resultado de la sustracción y por tanto es un valor numérico. Sin embargo, ni una ni otra son leyes, veamos el por qué:
La expresión a-b que acostumbramos a reconocer como la operatividad de la sustracción por no aparecer el signo + sino el signo - si aplicamos el ya conocido convenio de notación (ver publicaciones anteriores) a-b=a+(-b) nos damos cuenta de que en realidad estamos en presencia de la ley adición, y en ese sentido lo que ocurre es que estaríamos obteniendo la suma (resultado de la adición) de un número con el opuesto del otro. Es claro, que en dicha expresión se están articulando la definición de ley de composición interna adición (clausura de la adición) con la definición de elemento opuesto anteriormente planteada, en este caso, al ejecutar la operatividad vinculada a ambas definiciones da la impresión de que un número considerado mayor reduce respecto del otro considerado menor y de allí la percepción de resta o de que al mayor se le está sustrayendo una porción. Cuando estamos en bachillerato y conocemos conjuntos numérico superiores al conjunto de los números naturales, la comprensión de este hecho se puede apoyar el la relación de orden menor que y darnos cuenta que el elemento resultante de esta operatividad es más negativo o positivo dependiendo de la regla de los signos para la adición.
En cuanto a la división ocurre un hecho similar, salvo que en este caso se deben tener presentes las definiciones de ley de composición interna multiplicación (clausura de la multiplicación) y la de elemento inverso, por cuanto lo que ocurre es una operatividad vinculada a las mismas, a pesar de que en la expresión aparezca el signo ÷ que tradicionalmente identifica a la división, lo que realmente ocurre es una multiplicación de un número por el inverso de otro, hecho que se puede visualizar simbólicamente como sigue:
La expresión a÷b se acostumbra a representar por a/b y por eso se piensa que a (numerador o dividendo) se divide o parte tantas veces en porciones exactas como indica b (denominador o divisor), no obstante por el convenio de notación (ver publicaciones anteriores) a/b=a.1/b nos damos cuenta de que efectivamente se trata de una multiplicación con una operatividad articulada con las definiciones antes mencionadas.
Adicionalmente, es de hacer notar que si bien en los textos de bachillerato (en los universitarios de Álgebra Abstracta se aclara muy bien) se plantean propiedades para las leyes adición y multiplicación no aparecen propiedades para la sustracción y división, eso debería darnos la primera pista de claridad aunque oportunamente no se enfatiza en eso en el referido nivel educativo. Por otro lado, en el ámbito universitario se puede evidenciar que lo expuesto se aprende con tal rigor en las asignaturas relacionadas con el Álgebra Abstracta desde los primeros semestres de la carrera, sin embargo, algo ocurre cuando debe transferirse este saber en las demás subáreas de la Matemática, por cuanto en mi experiencia he observado que no se procura profundizar al respecto, hecho que mantiene de cierta forma aisladas las diferentes subáreas cuando se trata de una sola ciencia.
La presentación de este saber matemático de una perspectiva detallada y reflexiva es una oportunidad para brindar un espacio de intercambio para la toma de conciencia por parte de los actores educativos en la vía de generar transformaciones necesarias a la manera en la cual estamos facilitando los conocimientos de esta importante ciencia. En este sentido, es menester en primer lugar desaprender las tradicionales formas de enseñanza y apropiarse de una visión acompañada de métodos y estrategias que permitan dar a conocer la misma desde su formalidad, y a pesar de que es válida la premisa de que el mismo debe adecuarse a la edad de los estudiantes, también es cierto de que debemos dejar de subestimarlos creyendo que debemos simplificar (y hasta banalizar) el saber compartido con la excusa de que éstos lo comprendan en operatividad sacrificando en este proceso la esencia y valor teórico inherente al mismo.
Debo destacar que en la oportunidad que tuve de educar Matemática en bachillerato tuve por costumbre ser minuciosa y llamar a las cosas por su nombre, en el caso de las operaciones matemáticas era difícil seguir en lo tradicional sin hablarles de las leyes de composición interna y sus expresiones algebraicas tal como son, aclarando que se tienen las leyes adición y multiplicación con operatividades vinculadas a las propiedades y elementos distinguidos presentados en esta publicación. En el caso de las operatividades tradicionales sustracción y división se les explicó en detalle que las mismas no son leyes sino operatividades que provienen de la articulación entre las definiciones de ley interna (clausura) y elementos simétricos (particularizados en cada caso como se explicó en este post. Los resultados académicos fueron sorprendentes obteniendo en una mayoría notable muy buenos resultados de aprobación y comprensión de los conceptos facilitados, lo que eventualmente fue motivación para muchos para optar por carreras universitarias en Matemática y afines.
En el caso de los estudiantes universitarios, facilitando distintas asignaturas de la carrera de educación mención Matemática, se procuró siempre la integración de saberes de las diferentes subáreas que la conforman, esto sin duda garantiza un comprensión más profunda de la misma. Estos aprendices, por cursar adecuadamente las asignaturas relacionadas con el Álgebra Abstracta les resultó más sencillo entender lo referido a la visión tradicional de las operaciones matemáticas.
En las próximas publicaciones, seguiremos explorando otros saberes matemáticos desde la postura educativa y reflexiva, saludos y éxitos para todos los lectores y académicos de esta comunidad.
Texto original redactado desde la visión de @reinaseq
Texto original redactado desde la visión de @reinaseq
Referencia
Rojo, A. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Animaciones creadas por @reinaseq mediante la aplicación Gif Maker para Android disponible en Google Play Store. Las diapositivas fueron diseñadas por @reinaseq en el editor de presentaciones Microsoft Powerpoint 2013 con información adaptada de Rojo (2001). Todos los separadores, banners e imágenes estáticas de este artículo son diseñadas en el editor de presentaciones Microsoft Powerpoint 2013, ajustadas y recortadas en Paint por @reinaseq.
Si estás interesado en contenidos sobre Ciencia, Tecnología, Ingeniería y Matemática, consulta las etiquetas #STEM-Espanol y #SteemSTEM, las cuales puedes utilizar para publicar contenidos en estas áreas. Puedes unirte al servidor de Discord de STEM-Espanol para participar en nuestra comunidad y consultar los reportes semanales publicados por @STEM-Espanol. Te esperamos!!
Si estás interesado en contenidos sobre Ciencia, Tecnología, Ingeniería y Matemática, consulta las etiquetas #STEM-Espanol y #SteemSTEM, las cuales puedes utilizar para publicar contenidos en estas áreas. Puedes unirte al servidor de Discord de STEM-Espanol para participar en nuestra comunidad y consultar los reportes semanales publicados por @STEM-Espanol. Te esperamos!!
- Normas STEM-Espanol
- Directrices sobre normas de derechos de autor
- Servidor Discord #STEM-Espanol
- Para unirte al trail de STEM-Espanol
- Vota por @stem.witness como Testigo aquí
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Siempre me encantó en mis profesores de cálculo, álgebra y geometría esa forma de explicar en donde se empezará desde el origen del argumento, pasando por todas las bases teóricas que fundamentan el tema, hasta incluso demostrar algunos teoremas y corolarios que le dan mas firmeza al aprendizaje. Si es verdad que tenía algunos colegas estudiantes amigos de la época que me decían: "Nosotros vamos hacer ingenieros no necesitamos de ese tipo de explicaciones tan profundas". Claro está yo difería entre ellos, ya que soy de los que pienso que mientras más conocimiento tengamos, más será nuestro desarrollo en el desenvolvimiento de nuestra profesión. Ahora que leo tu post siento esa misma satisfacción de cuando era aprendiz en la universidad por diversas razones: Tocas las operaciones elementales como la suma, resta, multiplicación y división, y le buscas su origen de existencia y sentido matemático dentro de la teoría de funciones, llevas un orden y disciplina impecable en el desarrollo de la temática, asunto primordial para el que desee aprender sobre el tópico si decide tomar la lectura del artículo, y por último el desarrollo de imágenes que ilustran las demostraciones y fundamentan las leyes de Composición Interna. Me alegra amiga que hayas podido resolver tu problema de conexión del internet, ya que a partir de este momento que volviste a deleitarnos con tus publicaciones estaré atento a tus publicaciones sobre matemática. Saludos y que continúen los éxitos.
Muchísimas gracias @carlos84 por tus generosas palabras y de igual manera celebro tu visión de explorar más allá de lo meramente instrumental de la ciencia, tienes toda la razón al afirmar que es muy importante comprender en detalle cada concepto matemático compartido con propósito educativo. La Matemática es una ciencia tan flexible que se adapta plenamente a las necesidades del perfil profesional donde esté involucrada, en este sentido, los ingenieros la requieren para la creación, comprensión y precisión de los diferentes procesos que impulsan, todo ello dependiendo de la especialidad en la cual se formen (eléctrica, civil, industrial, mecánica, telecomunicaciones, entre otras). Por otra parte el educador necesita comprender todos los detalles y fundamentos que la sustentan para poder garantizar una formación idónea de la población estudiantil que esté formando, y en el caso de los Matemáticos Puros, la requieren para investigar y desarrollar nuevas teorías, teoremas y sistemas axiomáticos que permitan comprender lo que aún la ciencia no ha resuelto. Como quiera que sea, es muy importante que la misma se estudie y comprenda plenamente para apoyar los diferentes enfoques en la cuales se utilizan para el bienestar de la humanidad. En cuanto a mi problema de conectividad sigue inestable, afortunadamente pude compartir esta publicación y espero poder seguir activa y poder compartir con todos. Agradecida por tu valioso aporte, saludos fraternos amigo!!
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by reinaseq from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Hi @reinaseq!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Votado por el trail @team-mexico
Canal Discord ¡Te esperamos!
Delegaciones para @team-mexico ¡Ayúdanos a crecer!
10 SP - 25 SP - 50 SP - 100 SP - 150 SP- Mas información.
.png)
Hola @reinaseq, felicidades por este post, como estudiante me pareció bastante útil (ojala lo hubiese leído cuando cursaba los primeros cursos de matemáticas de la universidad). Me gusto mucho la explicación acerca de la "resta" y la división. Personalmente opino que este tipo de fundamentos deben ser explicados con muy buena metodología, espero que algún día los gobiernos, en especial de latino américa, logren reformar el sistema y de esta forma hacer que los estudiantes cada vez tengan mejores bases conceptuales. Muchas gracias por compartir este contenido, saludos.
Hola @aleestra, muy agradecida por tu valoración, lo que planteas es prácticamente propósito fundamental en la Agenda ONU 2030, en su ODS4 se establece trabajar por una educación de calidad lo cual pasa por formar educadores calificados que brinden los saberes del área disciplinar que faciliten desde su máxima comprensión. Las nociones fundamentales de la Matemática son de gran importancia para la comprensión adecuada de saberes más avanzados, lo que comparto es parte del pensum de estudios de la Licenciatura en Educación Mención Matemática en muchas universidades, ciertamente me he percatado que en los pensum de estudio de Ingeniería no aparecen asignaturas relacionadas con el Álgebra Abstracta, en muchos casos sólo estudian Álgebra Lineal por la gran utilidad que la misma tiene en los procesos que desarrollan, pero ciertamente, la curiosidad natural de los seres humanos nos debe invitar a seguir explorando más allá de las aulas de clase donde nos formamos. Gracias por leer y aportar a mi publicación, saludos fraternos!!
Reina querida, el mundo necesita más profesores apasionados como tú... Que no hubiera dado por estar en una de tus aulas. Dios te bendiga!
Muchísimas gracias por tus generosas palabras, son una gran motivación, gracias por revisar mi aporte, saludos fraternos @yrmaleza!!
Cómo me he nutrido de tu óptica llena de entusiasmo. Te confieso que la matemática nunca me fue bien explicada... Creo que solo recibí dictados autómatas, razón por la cual creo no desarrollé amor por la misma y hoy quisiera retomar un aula aunque sea a nivel de curso para comprender bien todo lo que explicas con tal pasión. Apuesto por un mundo mejor lleno de salones guiados por profesores como tú... Un abrazo @reinaseq
Amiga @talmid, muy agradecida por tan conmovedoras palabras, lo que indicas ciertamente nos tiene que llamar a la reflexión a todos los profesores de Matemática por cuanto recibimos una formación de altura para ser educadores de esta área científica y cuando vamos al campo laboral nos dejamos arrastrar por la tradicionalidad y la costumbre, hecho que no necesariamente es compatible con la formación que recibimos para hacerlo bien, ergo muchos estudiantes no logran sentir el llamado para el estudio de la Matemática y carreras afines por la forma como se encuentra estigmatizada. Muy oportuno y reflexivo comentario, saludos fraternos y bendiciones!!
Quedé atrapada con tu introducción, y luego cuando leí el post, comprendí exactamente lo que quisiste decir al inicio. Fue como si me quitaran una venda de los ojos, o como si descubriera que me engañaron toda la vida y hoy veo la realidad...jeje.
Gracias por revisar mi aporte @ivymalifred, casualmente lo que experimentas es la misma sensación que tuve cuando estudié estos saberes en los primeros semestres de mi carrera, y eso sin duda sigue siendo hoy por hoy una alerta para que desde bachillerato comencemos a hablar claro a nuestros estudiantes y facilitar esta ciencia tan importante como debe ser, evitando caer en procesos algorítmicos y mecanicistas sin sentido que por demás mantienen la falsa idea de que la Matemática es difícil, me alegra mucho que hayas comprendido lo que quise manifestar, saludos fraternos y bendiciones!!
En definitiva, los docentes como pilares de la educación debemos reflexionar sobre la forma como esta está siendo llevada. Te invito a que revises esta publicación https://steemit.com/stem-espanol/@eliaschess333/stem-chess-el-ajedrez-en-la-educacion-desde-una-vision-que-transversaliza-al-proyecto-stem donde explico entre otras cosas, las ideas principales de lo que fue la propuesta resultante de mi tesis de maestría en educación superior.
Ya para finalizar, excelente la explicación del tema Leyes de Composición Interna, me ha sido de gran utilidad, dado que en Perú que es donde me encuentro, tengo el reto de explicar Matemática a estudiantes de bachillerato, y dominar los términos correctos es fundamental.
Saludos y felicidades!
Hola @eliaschess333, muchas gracias por leer mi aporte, coincido contigo en la necesidad de transformar la forma como es percibido el educador en Matemática, y eso pasa precisamente por que cada uno de nosotros cambiemos la forma de diálogo en el aula de clases, esto es, acabar con el mito de que la Matemática es difícil y que todo es demasiado complicado, eso fomenta prejuicios que a la larga generan bloqueos hacia el aprendizaje de la misma y trae como consecuencia que los estudiantes la estudien para pasar con cualquier calificación y no por aprender que es realmente el gran propósito. Por otro lado, hay que abandonar los recursos mnemotécnicos que comprometen la formalidad del lenguaje matemático, a veces se asumen, como el caso que di de la propiedad distributiva pensando que se hace más fácil para el estudiante pero se sacrifica mucho en cuanto a la formalidad de esta ciencia. Me alegro que consideres este aporte como apoyo a tu actividad docente, es un gran halago, saludos fraternos!!
PD: Revisé tu aporte relacionado con el ajedrez, me pareció excepcional, recuerdo que cuando era estudiante en la universidad, era muy común en la Biblioteca de Matemática observar otros compañeros estudiantes de la misma carrera realizar intercambios mediante el juego de ajedrez, incluso era tan motivador que hasta nuestros mismos profesores participaban y nos acompañaban en esas jornadas, de igual manera organizábamos torneos amistosos. Era de conocimiento general para nosotros que el ajedrez promueve el desarrollo de las habilidades del pensamiento, especialmente el razonamiento abstracto lo cual favorecía significativamente el estudio de la Matemática, en particular a pesar de no saber jugar muy bien coincido plenamente con esas afirmaciones las cuales tienen fundamentación científica. Creo que para la comunidad de STEM-espanol sería de gran beneficio establecer intercambios de ajedrez virtual, no se si Discord (técnicamente hablando) lo permite, lo cierto es que otra de las bondades de este juego es que favorece la socialización!! Interesante intercambio de puntos de vistas educativos, saludos fraternos!!
*Para el aprendizaje matemático es necesario tener claro las nociones fundamentales relacionadas a las leyes de composición interna, ya que de allí parte toda nuestra debida comprensión hacia el mundo de las matemáticas, por lo que recomiendo ampliamente tu publicación a cualquier persona interesada en esta área, pero sobre todo a aquellas personas que se inician en el campo de la docencia debido a que desarrollas extraordinariamente cada uno de los tópicos planteados, utilizando magistralmente excelentes imágenes para la consolidación del aprendizaje ofrecido.
*Pienso estimada amiga que publicaciones como la que nos ofreces es la razón de esta comunidad de steemit, sobre todo la de stem-espanol la cual se preocupa por mejorar la enseñanza en las áreas STEM, y tú claramente nos ofreces las nociones fundamentales sobre la debida enseñanza de esta maravillosa y apasionante ciencia (matemática).
*Poder tener el placer de leer tus palabras me hace valorar nuestro papel en la enseñanza y sentir que no estás solo en este inmenso universo de prejuicios educacionales, en nuestro desarrollo universitario nos encontramos con profesores de conductas variadas en cuanto a su manera y forma de transmitir sus conocimientos, pero siempre he tratado de recopilar de todos ellos lo más resaltante tanto positiva como negativamente, para corregir debilidades, sin dejar a un lado que como docentes siempre debemos tener un asiento entre nuestros estudiantes para podernos observar desde su perspectiva que considero el mayor de los prejuicios de la mayoría de los docentes debido a que no lo realizan, eres un ejemplo a seguir en el modelo educacional, ya que tienes esa capacidad que pocos tienen en esta área y es la de poder ver desde los ojos de sus estudiantes, allí siempre estará el éxito de cualquier tipo de aprendizaje.
Espero seguir compartiendo conocimientos contigo en esta grandiosa plataforma y desde la trinchera de stem-espanol, los cuales nos ayudan a crecer tanto a nosotros y con ello a los que nos leen. Saludos fraternos mi estimada, éxitos por tu sabiduría.
Hola amigo @rbalzan79, enormemente agradecida por la bondad de tus palabras, las mismas me comprometen a seguir mejorando y tratando de brindar lo mejor cada día. En lo que respectas a las diversidad de perspectivas docentes coincido contigo, es muy cierto que cada educador de Matemática y otras áreas de acuerdo a su propia esencia como ser humano asume una forma muy particular de enseñar y eso es altamente valioso, sin embargo, a pasar de la forma muy particular y autentica de educar debe prevalecer el respeto al saber que se facilita, en particular en el caso de la Matemática se debe garantizar la formalidad del lenguaje que se emplea en tanto que el mismo es universal, esto es, sin importar la lengua nativa la simbología de esta área científica es única y su identificación tambien lo es. Afortunadamente, en el mundo a partir de la Agenda ONU 2030 se están acelerando interesantes procesos de transformación entre los cuales la Educación es protagonista, de allí que es nuestro deber ser mediadores para lograr cambios significativos y productivos en la Educación Matemática y científica en general. Nuevamente te agradezco la lectura de mi publicación y dejar aportes reflexivos y constructivos para el debate, saludos fraternos amigo!!
Muy interesante tu publicación, me gusto mucho tu explicación fue bastante educativa y entendible, pienso que sería una forma muy versátil de enseñar las matemáticas, porque si mi área de conocimiento el plato fuerte no es la matemáticas y logre entender, que bueno seria de aquellos que les encanta este tipo de estudios.
Fue muy ameno leer tu publicación te deseo muchos éxitos.
Hola @felixrodriguez, me alegra mucho haber logrado la comprensión de este saber por un colega STEM de una carrera científica hermana, es un honor llegar a muchas personas con los saberes compartidos, eso vale más que cualquier título porque se trata de eliminar las fronteras científicas, muy agradecida por tu motivador comentario, saludos fraternos!!
muy didáctico y ameno, gracias
Gracias por tu valoración, saludos!!