
Saludos a toda la comunidad de Steemit, siguiendo con la temática relativa a las Relaciones de Equivalencia, en esta publicación se presentarán y demostrarán teoremas y propiedades de gran relevancia que le otorgan a este caso particular de las Relaciones Binarias el sustento teórico necesario para poder aplicar estos conceptos en el desarrollo de otros saberes matemáticos.
Es pertinente que se tengan a disposición los conocimientos previamente publicados, con el propósito de garantizar la máxima comprensión de lo que aquí se presenta las mismas estarán disponibles al final de este post a través de vínculos direccionados a las mismas.

El Teorema Fundamental de las Relaciones de Equivalencia es gran importancia, en tanto que con el mismo se le da cuerpo firme y sólido al hecho de que al definir una relación de equivalencia en un conjunto no vacío, la misma establece una partición de este en clases de equivalencia, razón por la cual se procederá a enunciar formalmente y demostrar.
Teorema
Sea la relación de equivalencia ~ definida en A≠∅, esto indica que exista un I⊂A de manera que para cualquier elemento u∈I existe una clase de equivalencia subconjunto de A para lo cual se cumple lo siguiente:
Vale destacar que I es el conjunto de índices que se forma al seleccionar un elemento único o representante de cada clase de equivalencia.
Antes de proceder a la demostración conviene tener en cuenta que el enunciado del teorema tiene aspectos de gran importancia que se considerarán como hipótesis en el proceso de comprobar las proposiciones I, II, III, IV y V.
Demostración
∀u∈I⟹Ku≠∅
En esta parte recordemos que por hipótesis A≠∅ y en el mismo se ha definido una relación de equivalencia ~, por lo cual se da por hecho que se cumplen las propiedades de reflexividad, simetría y transitividad. Procedamos
Si A≠∅⟹∃x∈A, esto es obvio en tanto que si es un conjunto no vacío debe tener al menos un elemento.
⟹x~x, por hipótesis se cumple la propiedad reflexiva
⟹x∈Kx, por definición de clase de equivalencia
⟹Kx≠∅, ∀x∈A, si tiene al menos un elemento la clase de equivalencia es no vacía
Ahora bien como I⊂A
u∈I⟹u∈A, por definición de inclusión de conjuntos
⟹u~u, por hipótesis se cumple la propiedad reflexiva
⟹u∈Ku, por definición de clase de equivalencia
⟹Ku≠∅, como tiene al menos un elemento la clase de equivalencia es no vacía
∴ Se cumple que ∀u∈I⟹Ku≠∅∎
a∼a'⟺a y a' pertenecen a la misma Ku
El conectivo principal de la proposición es un condicional por lo cual se debe demostrar el teorema directo y el teorema recíproco.
Teorema Directo
¿a∼a'⟹a y a' pertenecen a la misma Ku?
Demostrando
a∼a'⟹a∈Ka ∧ a'∈Ka, por definición de clase de equivalencia
Luego u∈I ∧ u∈Ka tenemos que a y a' pertenecen a la misma clase de equivalencia
∴ Se cumple que a∼a'⟹a y a' pertenecen a la misma Ku
Teorema Recíproco
¿ a y a^' pertenecen a la misma Ku⟹ a∼a'?
Demostrando
a y a' pertenecen a la misma Ku⟹a∼u ∧ a'∼u, por definición de clase de equivalencia
⟹a∼u∧u∼a', por hipótesis se cumple la propiedad simétrica
⟹a∼a', por hipótesis se cumple la propiedad transitiva
∴ Se cumple que si a y a' pertenecen a la misma Ku⟹ a∼a'
∴ Se cumple que a∼a'⟺a y a' pertenecen a la misma Ku∎
Ku∩Kv≠∅⟹Ku=Kv
En este caso se pide comprobar que clases de equivalencia no disjuntas son iguales. Como se puede observar estamos en presencia de una proposición condicional por lo cual lo que está a la izquierda del conectivo es la hipótesis y lo que se encuentra a la derecha es la tesis, es decir lo que se debe comprobar.
Demostrando
Considerando la hipótesis tenemos
Ku∩Kv≠∅⇒∃a∈(Ku∩Kv), si es un conjunto no vacío debe tener al menos un elemento.
⇒a∈Ku ∧ a∈Kv, por definición de intersección de conjuntos
⇒a∼u∧a∼v, por definición de clase de equivalencia
⇒u∼a∧a∼v, por hipótesis se cumple la propiedad simétrica (1)
Por otro lado, consideremos b∈Ku⇒b∼u (2)
⇒u∼v, por hipótesis se cumple la propiedad transitiva (1)
⇒u∼v∧b∼u, por afirmación (2)
⇒b∼u∧u∼v, por ley lógica conmutativa de la conjunción
⇒b∼v, por hipótesis se cumple la propiedad transitiva
⇒b∈Kv, por definición de clase de equivalencia
⇒Ku⊂Ku, por definición de inclusión de conjuntos
Para llegar a la igualdad de estos conjuntos debemos comprobar igualmente que la clase de v está contenida en el conjunto clase de u. en este caso se procede de forma análoga pero en la proposición (2) se considerará la pertenencia del elemento al conjunto clase de v, por lo cual en la comprobación faltante retomaremos el proceso a partir de ese punto específico como sigue
Considerando b∈Kv⇒b∼v (2)
⇒a∼u∧a∼v⇒a∼v∧a∼u, por ley lógica conmutativa de la conjunción
⇒v∼a∧a∼u, por hipótesis se cumple la propiedad simétrica (1)
⇒v∼u, por hipótesis se cumple la propiedad transitiva (1)
⇒v∼u∧b∼v, por afirmación (2)
⇒b∼v∧v∼u, por ley lógica conmutativa de la conjunción
⇒b∼u, por hipótesis se cumple la propiedad transitiva
⇒b∈Ku, por definición de clase de equivalencia
⇒Kv⊂Ku, por definición de inclusión de conjuntos
∴Por cumplirse Ku⊂Kv y Kv⊂Ku debido a las demostraciones anteriores se cumple que Ku=Kv, por definición de igualdad de conjuntos∎
u≠v⟹Ku∩Ku=∅
Al igual que en la proposición anterior, estamos en presencia de un condicional, es decir, a la izquierda del conectivo tenemos la hipótesis y a la derecha la tesis, justo lo que se debe demostrar. Para aclarar, se debe comprobar que dos clases de equivalencia cualesquiera son disjuntas si son diferentes sus respectivos índices.
Para esta comprobación procedemos por el Método de Reducción al Absurdo en el cual se asume que la hipótesis es verdadera y se niega la tesis, posteriormente si nos encontramos con una afirmación considerada absurda o contradictoria se concluye que la misma se deriva por haber negado la tesis por lo cual se acepta como demostrada y verdadera la proposición condicional inicial, es decir, la que queremos comprobar.
Demostrando
Por el Método de Reducción al Absurdo suponemos que
Ku∩Kv≠∅⇒∃a∈(Ku∩Kv), si es un conjunto no vacío debe tener al menos un elemento.
⇒a∈Ku ∧ a∈Kv, por definición de intersección de conjuntos
⇒a∼u∧a∼v, por definición de clase de equivalencia
⇒u∼a∧a∼v, por hipótesis se cumple la propiedad simétrica
⇒u∼v, por hipótesis se cumple la propiedad transitiva
⇒u∈Kv, por definición de clase de equivalencia (Absurdo)
La derivación anterior es absurda por cuanto contradice la definición de conjunto de índices, la misma se genera por haber negado la tesis, luego la tesis es verdadera.
∴ Se cumple que u≠v⟹Ku∩Kv=∅∎
∀a∈A,∃u∈I/a∈Ku
Demostrando
Consideremos que a∈A⇒a∼a, por hipótesis se cumple la propiedad reflexiva
⇒a∈Ka, por definición de clase de equivalencia (1)
Por otro lado
⇒u∈Ka, por definición de conjunto de índice, se escoge u como elemento canónico o representante de la clase de equivalencia
Esto implica que Ka=Ku
Luego la proposición (1) es a∈Ku∎
Finalmente, por las demostraciones I, II, III, IV y V queda demostrado el Teorema Fundamental de las Relaciones de Equivalencia∎

Sea el conjunto {Ku/u∈I} una partición de A, esto indica que en el conjunto A influye una relación de equivalencia, por lo cual se define como propiedad el hecho de que dos elementos del conjunto A están relacionados si y sólo si ambos elementos pertenecen al mismo subconjunto de la partición, es decir, pertenecen a la misma clase de equivalencia. En símbolos es
(a,b)∈R⟺a y b pertenecen a la misma Ku
Para demostrar esta propiedad, basta con verificar que R es una relación de equivalencia, es decir, que cumple con las propiedades de reflexividad, simetría y transitividad. Procedamos:
Reflexividad:
Demostrando
∀a∈A⇒∃u∈I/a∈Ku, por definición de la partición de A
⇒a∈Ku ∧ a∈Ku, por ley lógica de idempotencia de la conjunción
⇒(a,a)∈R, por definición de la relación R
∴ La relación R es Reflexiva, por definición de reflexividad.
Simetría:
Demostrando
(a,b)∈R⇒a y b pertenecen a la misma Ku, por definición de la relación R
⇒b y a pertenecen a la misma Ku, por conmutatividad de la conjunción
⇒(b,a)∈R, por definición de la relación R
∴ La relación R es Simétrica, por definición de simetría.
Transitividad:
Demostrando
(a,b)∈R∧(b,c)∈R⇒(a∈Ku ∧ b∈Ku) ∧ (b∈Ku ∧ c∈Ku), por definición de la relación R
⇒a∈Ku ∧ (b∈Ku ∧ b∈Ku) ∧ c∈Ku, por ley lógica asociativa de la conjunción
⇒(a∈Ku ∧ b∈Ku) ∧ c∈Ku, por ley lógica de idempotencia de la conjunción
⇒a∈Ku ∧ (b∈Ku∧ c∈Ku), por ley lógica asociativa de la conjunción
⇒a∈Ku ∧ (c∈Ku ∧ b∈Ku), por ley lógica conmutativa de la conjunción
⇒(a∈Ku ∧ c∈Ku) ∧ b∈Ku, por ley lógica asociativa de la conjunción
⇒a∈Ku ∧ c∈Ku, por ley lógica de simplificación
⇒(a,c)∈R, por definición de la relación R
∴ La relación R es Transitiva, por definición de transitividad.
∴ R es una relación de equivalencia, por definición de relación de equivalencia.∎

Sea R una relación definida en un conjunto A. En R se cumplen las siguientes propiedades:
R es simétrica ⇒ R-1 es simétrica
R es transitiva ⇒ R-1 es transitiva
R y S son transitivas ⇒ R∩S es transitiva
R y S son antisimétricas ⇒ R∩S es antisimétrica
Las propiedades como se puede observar se tratan de proposiciones condicionales, es decir tienen la forma hipótesis, conectivo condicional y tesis. Además, para sus demostraciones respectivas deben considerarse las definiciones de las propiedades implicadas en las mismas. A continuación se procederá con las comprobaciones.
R es simétrica ⇒ R-1 es simétrica
Demostrando
∀(a,b)∈R-1⇒(b,a)∈R, por definición de relación inversa
⇒(a,b)∈R, por hipótesis R es simétrica
⇒(b,a)∈R-1, por definición de relación inversa
∴ La relación R-1 es Simétrica, por definición de simetría∎
R es transitiva ⇒ R-1 es transitiva
Demostrando
∀(a,b)∈R-1 ∧ (b,c)∈R-1⇒(b,a)∈R ∧ (c,b)∈R, por definición de relación inversa
⇒(c,b)∈R ∧ (b,a)∈R, por ley lógica conmutativa de la conjunción
⇒(c,a)∈R, por hipótesis R es transitiva
⇒(a,c)∈R-1, por definición de relación inversa
∴ La relación R-1 es Transitiva, por definición de transitividad∎
R y S son transitivas ⇒ R∩S es transitiva
Demostrando
∀(a,b)∈(R∩S)∧(b,c)∈(R∩S)⇒[(a,b)∈R∧(a,b)∈S]∧[(b,c)∈R∧(b,c)∈S], por definición de intersección de conjuntos
⇒(a,b)∈R∧[(a,b)∈S∧(b,c)∈R]∧(b,c)∈S, por asociatividad de la conjunción
⇒(a,b)∈R∧[(b,c)∈R∧(a,b)∈S]∧(b,c)∈S, por conmutatividad de la conjunción
⇒[(a,b)∈R∧(b,c)∈R]∧[(a,b)∈S∧(b,c)∈S], por asociatividad de la conjunción
⇒(a,c)∈R∧(a,c)∈S, por hipótesis R y S son transitivas
⇒(a,c)∈(R∩S), por definición de intersección de conjuntos
∴ La relación R∩S es Transitiva, por definición de transitividad∎
R y S son antisimétricas ⇒ R∩S es antisimétrica
Demostrando
∀(a,b)∈(R∩S)∧(b,a)∈(R∩S)⇒[(a,b)∈R∧(a,b)∈S]∧[(b,a)∈R∧(b,a)∈S], por definición de intersección de conjuntos
⇒a=b∧a=b, por hipótesis R y S son antisimétricas
⇒a=b, por ley lógica de idempotencia de la conjunción
∴ La relación R∩S es Antisimétrica, por definición de antisimetría∎

Las nociones que definen un concepto en Matemática son importantes, adicionalmente los teoremas y propiedades que se verifican en el referido ámbito le dan cuerpo y soporte teórico necesario para poder utilizarlos en el desarrollo de otros conceptos matemáticos. En el caso de las Relaciones de Equivalencia las demostraciones presentadas en esta oportunidad son fundamentales, en tanto que en el futuro permitirán comprender, entre otras cosas, el ¿por qué? de conjuntos numéricos por todos conocidos.
Nos leemos en la siguiente publicación, saludos y éxitos para todos los lectores y académicos de esta comunidad.

“Cómo es posible que la matemática, un producto del pensamiento humano independiente de la experiencia, se adapte tan admirablemente a los objetos de la realidad” - Albert Einstein.

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Todas las imágenes, separadores y banners de este artículo son de autoría propia diseñadas en el editor de presentaciones Microsoft Powerpoint 2013, ajustadas y recortadas en Paint.
Publicaciones Relacionadas


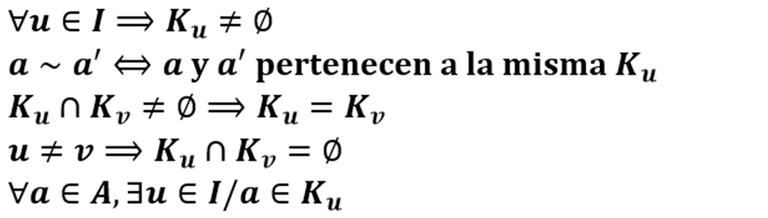
Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.Congratulations! This post has been upvoted from the communal account, @minnowsupport, by reinaseq from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Muchas gracias por su apoyo, saludos cordiales!!
¡Felicidades, #proconocimiento te valoró!
Has sido reconocido(a) por tu buen post por el Comité de Arbitraje y Valoración del Proyecto Conocimiento @proconocimiento.
Apoyamos y valoramos tu esfuerzo...
Proyecto Conocimiento es parte de la comunidad @provenezuela.
PionerosProducción Intelectual en habla hispana. en la plataforma #steemit en el reconocimiento y valoración a la
Muchas gracias por el invaluable apoyo, abrazos fraternos!!
Excelente publicacion amiga, muy buenas explicaciones y ejemplos sobre las relaciones de equivalencias, es muy importante como tu lo has hecho en este articulo, que se especifiquen las demostraciones paso a paso de cada definición matemática con sus respectivos ejemplos, un saludo y nos seguimos leyendo.
Muy agradecida por tu valoración @carlos84, en el caso del Álgebra hay que hacer esfuerzos por presentar los contenidos con mucha especificidad, cuesta mucho su comprensión en los estudiantes por su naturaleza abstracta!! Saludos cordiales!!