Creative Commons , CC-BY 4.0 혹은 CC-BY-SA 3.0이 걸려있으므로 자유롭게 사용 가능합니다.안녕하세요, @doctorbme 입니다. 오늘은 전염병 전파와 관련 요인, 전파 방지를 위한 전략 도출을 위한 수학적 모델링에 관한 개괄적 설명을 하고자 합니다. 본 글에서 사용할 이미지는
서론
치사율이 높은 바이러스/세균에 누군가 감염되었다면, 이 바이러스/세균은 지역사회에 심각한 위해를 가할 수 있을까요? 집단 감염을 통해 사회가 혼란과 붕괴에 이르게 될까요? 이에 대해서는 판단할 수 없습니다. 정보가 부족하기 때문입니다. 예를 들어 치사율이 높은 바이러스라고 하더라도 걸리자마자 5분만에 (사실 이럴리는 없겠지만요.) 사망하게 되고, 누군가 접촉할 기회를 잃어버린다면, 감염된 사람은 사망하겠지만 실제로 지역사회에 대한 위협은 현저히 적을 것입니다. 어떤 전염병이 지역사회에 유행하기 위해서는, 감염된 사람이 감염되지 않은 사람을 전파시킬 기회와 기간이 충분해야 합니다.
그렇다면 전염병에 걸린 사람이 모두다 죽는 것일까요? 그렇지도 않을 것입니다. 일부는 회복되고 살아남을 것입니다. 특히 현대 의학의 도움을 받는다면, 치사율은 좀 더 감소할지도 모릅니다. 회복이 된 상태에서 체내의 바이러스/세균 또한 완벽히 제거된 상태일 수도 있고 아니면 꾸준히 잠재적으로 가지고 있는 상태로 다른 사람을 전파시킬 수 있는 숙주로서 활동할 수도 있을 것입니다. 점점 생각해야할 파라미터들이 많아집니다.
개념
그러면 어떠한 전염병이 지역사회에 나타났다가 사라지는 과정에 대해 수학적 모델링을 통해 파악해볼 수 있을까요? 그렇습니다. 완벽하지는 않지만 일전에 한번 언급되었던 구획모델링(Compartment Modelling)을 이러한 과정의 묘사에 적용해볼 수 있습니다.
위키피디아의 Compartmental models in epidemiology(역학에서의 구획 모델링)에 따르면 이와 관련된 다양한 모델들이 존재합니다.
아주 간단한 모델을 볼까요?
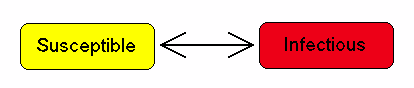
독감이나 감기와 같은 경우에는, 감염이 되었다 안되었다를 반복합니다. 이 모델은 독감이나 감기로 인한 사망을 가정하지 않습니다. 두 개의 구획(Susceptible/감염이 가능함 <-> Infectious/감염됨) 사이에서 사람들이 존재할 것입니다.
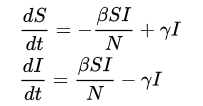
이는 위와 같은 간단한 일차(일계) 미분 방정식들의 집합으로 기술 가능합니다.
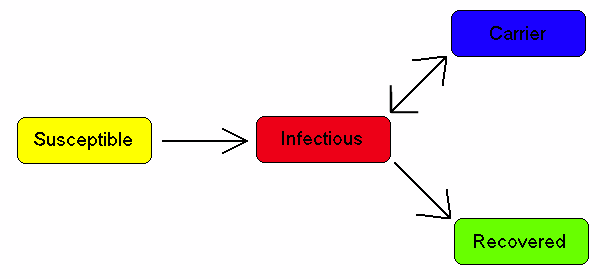
이런 경우는 어떨까요. 한번 걸리고 나면 면역력이 생기기는 하는데, 회복이 완전히 깨끗하게 된 경우(Recovered)와 뭔가 감염과 관련된 세균이나 바이러스를 가지고 쭉 사는 경우 (Carrier)로 나뉠 수 있습니다.

이런 경우에는 노출(Exposure)의 상태가 추가로 포함되었습니다. 감염될 수 있는 모든 사람이 걸린다기 보다는, 노출의 상황을 가정하여, 하나의 구획을 추가한 것입니다.
이러한 모델을 열심히 확장하다보면 아래와 같은 매우 복잡한 수학적 모델을 세울 수 있습니다. 참고문헌 2의 그림 1에서 나타낸 것으로 에볼라 바이러스의 전파 과정을 모델링한 것입니다. 이 모델에서는 백신을 맞은 상황인 V, 격리된 상황인 J, 이미 사망하였으나 아직 땅에 묻히지 않은 (따라서 고유 지역의 풍습을 반영한) D의 상태가 추가되었으며, 바이러스에 노출된 상황의 경우에는 (E) 노출되었으나 파악되지 않는 잠재 상황(E1)과, 파악이 가능한 잠재 상황(E2) 로 나누어 모델링 합니다.
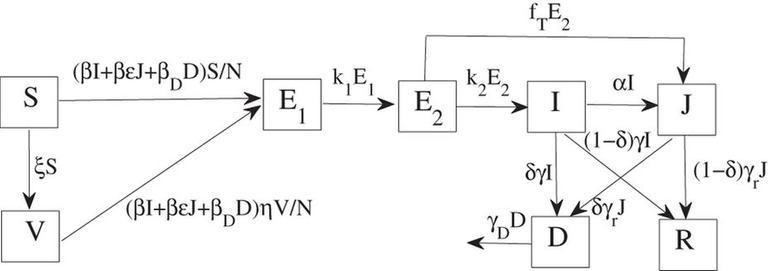
이렇게 다양한 상황을 가정하는 이유는, 실제 현상과 가급적 가까이 묘사하기 위함이며, 여러 파라미터들 중에서 개입이 가능한 파라미터가 변화하였을 때 모델의 결과가 어떻게 변하는지를 파악하여, 실제 전파 방지 정책 및 전략에 활용하기 위함입니다.
(참고문헌 2에 대해서는 후속 글에서 자세히 다루도록 하겠습니다.)
Basic Reproduction Number
이러한 모델의 특성을 파악하기 위해서는 다양한 방법론이나 인덱스가 사용될 수 있는데, 그 중 하나가 Basic Reproduction Number 입니다. Basic Reproduction Number, R0 는 역학을 위한 수학적 모델링에서 다양한 의미를 가집니다. 이는 질병에 감수성을 가진(susceptible) 집단에서, 이미 질병 감염이 있는 개인들에 의해, 이차 감염이 얼마나 생길 수 있을지에 해당하는 기대값을 반영합니다. 여기서 기대값이라는 의미는, 이차 감염에 원인이 되는 원래 감염된 개인이 처음 감염부터 회복이 될 때까지 평균적으로 얼마나 새롭게 전파하여 감염시킬 것인가에 대한 수치를 반영합니다. 따라서 R0<1 이면 결국 감염병의 유행이 없는 상태의 안정된 상태로, R0>1 이면 감염병의 유행이심해져서 결국 걷잡을 수 없는 상태에 빠져드는 것을 의미합니다. 참고문헌 3에서 자세히 잘 기술되어 있습니다. (사실 이 논문을 제대로 보기 위해서는 Nonlinear Control Theory 에서 다루는 Locally Asymptotic Stability와 Central Manifold Theorem에 대한 이해가 필요합니다. )
결국 실제 상황에 맞게 모델링을 해야하는 것이기 때문에, 모델에 포함된 파라미터를 찾는 것은 매우 중요한 이슈입니다. 파라미터를 찾다보면, Identifiability가 확보되지 않는 경우가 있는데, 이럴 경우에는 실제로 계산된 파라미터 값이 실제 현상에 근거하느냐, 역학적으로 말이 되는 것인지를 따져보아야 합니다. 수학적 모델은 수학적 파라미터의 값에 맞게 움직일 뿐, 이 파라미터들이 현실 세계에 대해 합리적인 범위에 있는지를 말해주지는 않기 때문입니다.
또한 Sensitivity Analysis를 통해, 각 파라미터들의 변화가 다른 파라미터들 혹은 모델의 안정성에 얼마만큼 영향을 끼치고 있는지를 파악해야합니다. 결국 dynamics를 묘사하는 것이기 때문에, 불안정하거나 수렴하지 않는 해(solution)가 존재하는 범위나 영역이 나타날 수 있기 때문입니다.
파라미터들이 잘 파악되면, 이제는 수학적 모델링을 바탕으로, 전염병 방지에 대한 다양한 전략과 정책에 대한 시뮬레이션을 해볼 수 있습니다. 특히 전염병 중에서도, 말라리아나 에볼라 바이러스 감염과 같은 경우에는 선진국보다는 개발도상국과 같은 나라에서 이슈가 되어, 한정된 가용 자원과 풍습, 문화적 차이를 반영하여 어떠한 방법을 활용해볼 수 있을지 파악하고, 진행 경과를 예측하는 데에 효과적으로 쓰일 수 있습니다.
결론
- 전염병의 전파에 관하여, 수학적 모델링이 가능합니다.
- 다양한 상황과 이에 대한 파라미터들을 가정할 수 있으며, 이에 따라 전파 양상의 예측과 전략/정책의 효과를 시뮬레이션하여 참고할 수 있습니다.
- 모델은 아름답지만, 현실 세계의 데이터와 합치시키기 위해서는 다양한 노력과 방법론이 요구됩니다.
특히 3에 관해서는 후속글에서, 에볼라 바이러스 전파에 대한 개입(intervention)효과 평가에 관한 모델링 논문(참고문헌 2)을 살펴보며 실제 연구를 진행하는데에 고려해야할 사항들에 대해 살펴보도록 하겠습니다. 감사합니다.
참고문헌(Reference)
[1] Compartmental models in epidemiology(역학에서의 구획 모델링)
[2] Mingwang Shen, Yanni Xiao & Libin Rong, Modeling the effect of comprehensive interventions on Ebola virus transmission, Scientific Reports volume 5, Article number: 15818 (2015), doi:10.1038/srep15818
[3] P.van den Driesschea, JamesWatmoughb, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences, Volume 180, Issues 1–2, November–December 2002, Pages 29-48


그래서 치사율이 높은건 병균입장에선 별로인 형태라고하죠 ㅎㅎㅎㅎ
말씀주신대로, 지역사회에 나쁜 영향을 얼마나 미칠 수 있는 있는지에 관한 요인은 적절한 치사율과 전파력, 잠복기 등이 모두 고려되기 때문에, 아무래도 너무 높은 치사율은 정말로 국소적인 영향만 줄 가능성이 높습니다.
오늘의 포스트를 보니 World of Warcraft라는 게임에서 발생했던 '오염된 피(Corrupted Blood)' 전염병 사건이 생각납니다.
치사율과 전염성이 강한 병이 발생했을 때 어떤 이는 치료를, 어떤 이는 너 죽고 나 죽자하며 전염에 일조를, 어떤 이는 홀로 고독사를 선택하기도 하고, 그 와중에 치료약이라며 가짜 약을 파는 사기꾼까지 있었음이 보고되었었는데요. -0- 그 결말은 '서버 리셋' 이었기 때문에 결말을 지켜보지 못한게 아쉽지만... 역학을 공부하시는 분들께서 관심을 가졌었다고 하시더라는걸 본 적 있습니다.
오늘도 흥미로운 내용 잘 읽고 갑니다! :D
그 사건은 매우 유명한 사건이기도 합니다. The untapped potential of virtual game worlds to shed light on real world epidemics 아마 이 논문일 겁니다. 아마도 알고계시겠지만, Lancet에 실린 기념비적인(?) 논문이라지요.
이쪽 분야의 (역학) 모델링은 1) 현상을 얼마나 잘 예측하고 묘사하느냐 2) 유추된 파라미터를 변경했을 때 과연 어떤 효과가 일어날 것이냐 3) 그래서 실제 전략/정책에 어떻게 반영할 것이냐 - 이렇게 3단계의 고민들이 이어져있다고 생각합니다. 사실 2번과 3번이 잘 이루어지면 좋은데, 현실 세계에서 모든 집단에 대해 실험을 할 수는 없으니, 제한점이 존재하긴 합니다. 물론 1번만 잘 해도 좋은 연구일 것입니다. (그러한 의미에서 Corrupted Blood 사건은 잘 통제된 느낌이긴 하죠. 물론 여러번 반복해서 살아날 수 있고 게임 상의 질병이 현실과의 질병과는 다르기 때문에, 아무래도 현실 세계에 직접적으로 반영하기는 조금 어렵겠지만 충분히 의미있다고 생각합니다.)
이미 알고계셨군요! 거기에 한 움큼 추가된 설명까지... @doctorbme님의 포스트에 들를 때마다 현실을 가정한 모델링 방법, 사고과정, 변인에 대한 철학을 배울 수 있어서 너무 감사드립니다.
조금이라도 도움이 되셨다니 다행입니다. 저도 감사드립니다. (--)(__)
여기서 어떤 주제에 대한 모델링 할때 매개변수 설정이 가장 어렵더군요.
매개변수에 따라서 그 결과가 달라지니깐요.
조사자의 객관적 관점 보다는 주관적 관점이 더 많이 반영되기 때문에 좀 어려운 것 같아요.
객관적 매개변수들을 기반으로 하더라고 그 매개변수의 갯수와 선택은 전적으로 조사자의 몫이니 깐 세밀히 보면 주관적 관점에 의한 모델링이 될 수 밖에 없는 것 같아요.
맞습니다. 매개변수를 어떻게 선택할 것이냐, 혹은 수많은 매개변수로 이루어진 집합의 부분집합을 어떻게 만들 것이냐는 상당히 중요한 이슈입니다. 물론 통계적으로 AIC나 BIC를 쓰면 조금 더 합리적인 선택이 가능하기는 하겠습니다만...
모델의 구조가 간단하면 놓치는 파라미터들이 많고, 모델의 구조가 복잡하면 과적합될 위험이 높으니, 적절하게 (주관적으로) 선택하는 것은 어쩌면 예술의 영역이 아닌가 하는 생각이 들 때도 있습니다. :)